Display Processor:It is interpreter or piece of hardware that converts display processor code into pictures. It is one of the four main parts of the display processor Parts of Display Processor
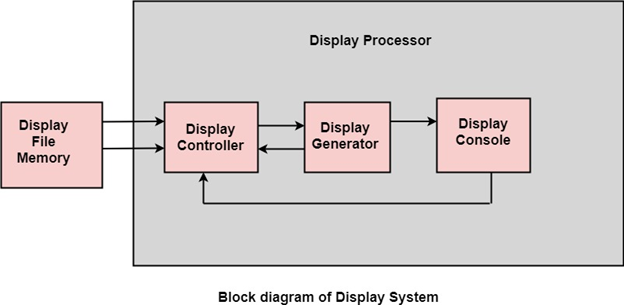 Display File Memory: It is used for generation of the picture. It is used for identification of graphic entities. Display Controller:
Display Generator:
Display Console: It contains CRT, Light Pen, and Keyboard and deflection system. The raster scan system is a combination of some processing units. It consists of the control processing unit (CPU) and a particular processor called a display controller. Display Controller controls the operation of the display device. It is also called a video controller. Working: The video controller in the output circuitry generates the horizontal and vertical drive signals so that the monitor can sweep. Its beam across the screen during raster scans. 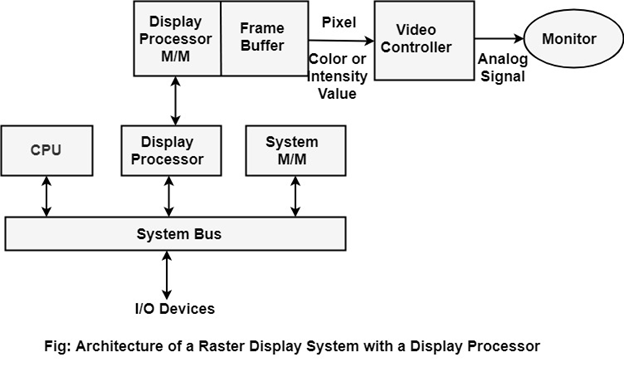 As fig showing that 2 registers (X register and Y register) are used to store the coordinate of the screen pixels. Assume that y values of the adjacent scan lines increased by 1 in an upward direction starting from 0 at the bottom of the screen to ymax at the top and along each scan line the screen pixel positions or x values are incremented by 1 from 0 at the leftmost position to xmax at the rightmost position. The origin is at the lowest left corner of the screen as in a standard Cartesian coordinate system. 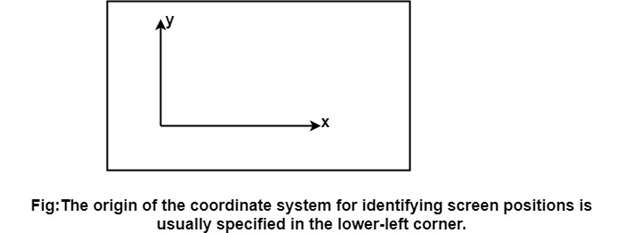 At the start of a Refresh Cycle: X register is set to 0 and y register is set to ymax. This (x, y') address is translated into a memory address of frame buffer where the color value for this pixel position is stored. The controller receives this color value (a binary no) from the frame buffer, breaks it up into three parts and sends each element to a separate Digital-to-Analog Converter (DAC). These voltages, in turn, controls the intensity of 3 e-beam that are focused at the (x, y) screen position by the horizontal and vertical drive signals. This process is repeated for each pixel along the top scan line, each time incrementing the X register by Y. As pixels on the first scan line are generated, the X register is incremented throughxmax. Then x register is reset to 0, and y register is decremented by 1 to access the next scan line. Pixel along each scan line is then processed, and the procedure is repeated for each successive scan line units pixels on the last scan line (y=0) are generated. For a display system employing a color look-up table frame buffer value is not directly used to control the CRT beam intensity. It is used as an index to find the three pixel-color value from the look-up table. This lookup operation is done for each pixel on every display cycle. As the time available to display or refresh a single pixel in the screen is too less, accessing the frame buffer every time for reading each pixel intensity value would consume more time what is allowed: 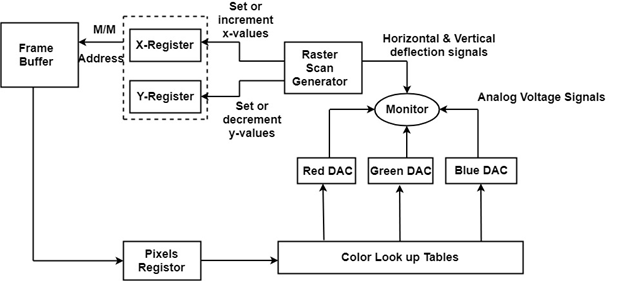 Multiple adjacent pixel values are fetched to the frame buffer in single access and stored in the register. After every allowable time gap, the one-pixel value is shifted out from the register to control the warm intensity for that pixel. The procedure is repeated with the next block of pixels,and so on, thus the whole group of pixels will be processed. Display Devices:The most commonly used display device is a video monitor. The operation of most video monitors based on CRT (Cathode Ray Tube). The following display devices are used:
Next TopicCathode Ray Tube (CRT)
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










