Reflection:It is a transformation which produces a mirror image of an object. The mirror image can be either about x-axis or y-axis. The object is rotated by180°. Types of Reflection:
1. Reflection about x-axis: The object can be reflected about x-axis with the help of the following matrix 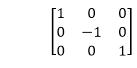
In this transformation value of x will remain same whereas the value of y will become negative. Following figures shows the reflection of the object axis. The object will lie another side of the x-axis. 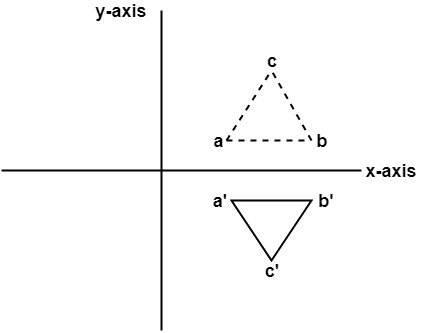
2. Reflection about y-axis: The object can be reflected about y-axis with the help of following transformation matrix 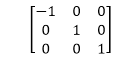
Here the values of x will be reversed, whereas the value of y will remain the same. The object will lie another side of the y-axis. The following figure shows the reflection about the y-axis 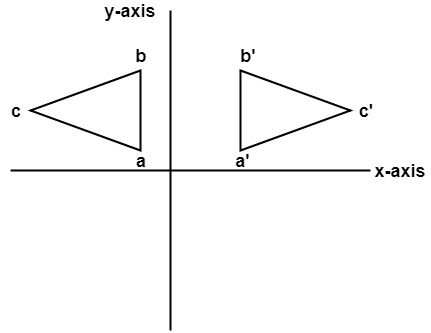
3. Reflection about an axis perpendicular to xy plane and passing through origin: 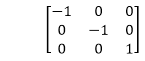
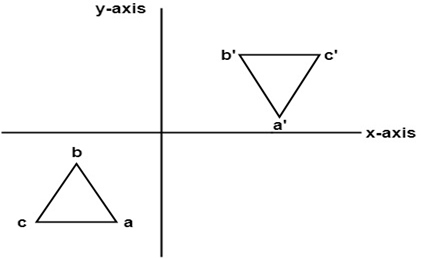
In this value of x and y both will be reversed. This is also called as half revolution about the origin. 4. Reflection about line y=x: The object may be reflected about line y = x with the help of following transformation matrix 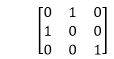
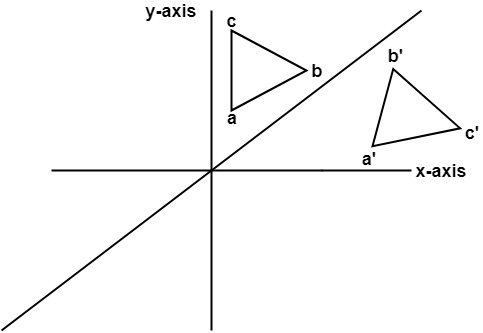
First of all, the object is rotated at 45°. The direction of rotation is clockwise. After it reflection is done concerning x-axis. The last step is the rotation of y=x back to its original position that is counterclockwise at 45°. Example: A triangle ABC is given. The coordinates of A, B, C are given as A (3 4) Find reflected position of triangle i.e., to the x-axis. Solution: 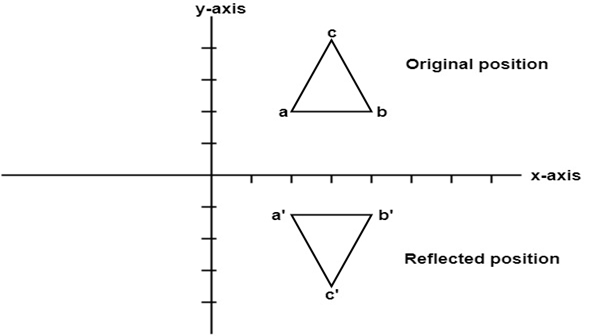

The a point coordinates after reflection 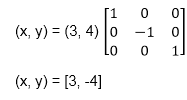
The b point coordinates after reflection 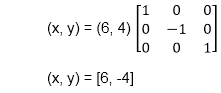
The coordinate of point c after reflection 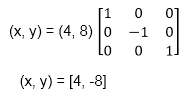
a (3, 4) becomes a1 (3, -4) Program to perform Mirror Reflection about a line:Output: 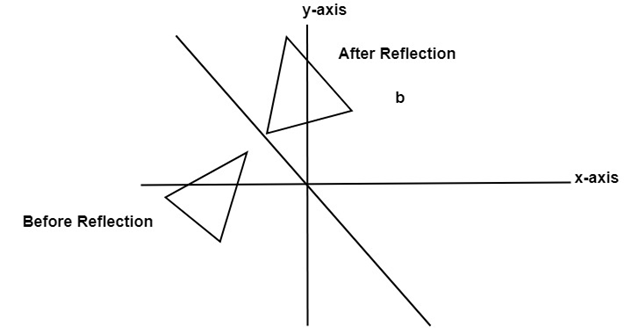
Next TopicShearing
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









