Defining a circle using Polynomial Method:

The first method defines a circle with the second-order polynomial equation as shown in fig:

y²=r²-x²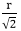
Where x = the x coordinate
y = the y coordinate
r = the circle radius

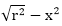With the method, each x coordinate in the sector, from 90° to 45°, is found by stepping x from 0 to Defining a circle using Polynomial Method

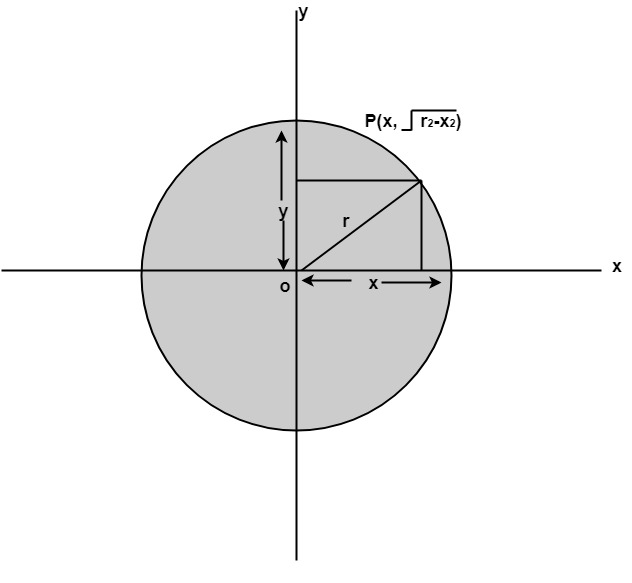
& each y coordinate is found by evaluating Defining a circle using Polynomial Method

for each step of x.

Algorithm:

Step1: Set the initial variables
r = circle radius
(h, k) = coordinates of circle center
x=o
I = step size
x_end= Defining a circle using Polynomial Method

Step2: Test to determine whether the entire circle has been scan-converted.

If x > x_end then stop.

Step3: Compute y = Defining a circle using Polynomial Method

Step4: Plot the eight points found by symmetry concerning the center (h, k) at the current (x, y) coordinates.

Plot (x + h, y +k) Plot (-x + h, -y + k)
Plot (y + h, x + k) Plot (-y + h, -x + k)
Plot (-y + h, x + k) Plot (y + h, -x + k)
Plot (-x + h, y + k) Plot (x + h, -y + k)

Step5: Increment x = x + i

Step6: Go to step (ii).

Program to draw a circle using Polynomial Method:

#include<graphics.h>
#include<conio.h>
#include<math.h>
voidsetPixel(int x, int y, int h, int k)
{
	putpixel(x+h, y+k, RED);
	putpixel(x+h, -y+k, RED);
	putpixel(-x+h, -y+k, RED);
	putpixel(-x+h, y+k, RED);
	putpixel(y+h, x+k, RED);
	putpixel(y+h, -x+k, RED);
	putpixel(-y+h, -x+k, RED);
	putpixel(-y+h, x+k, RED);
}
main()
{
	intgd=0, gm,h,k,r;
	double x,y,x2;
	h=200, k=200, r=100;
	initgraph(&gd, &gm, "C:\\TC\\BGI ");
	setbkcolor(WHITE);
	x=0,y=r;
	x2 = r/sqrt(2);
	while(x<=x2)
	{
		y = sqrt(r*r - x*x);
		setPixel(floor(x), floor(y), h,k);
		x += 1;
	}
	getch();
	closegraph();
	return 0;
}

Output: