Line Clipping:It is performed by using the line clipping algorithm. The line clipping algorithms are:
Cohen Sutherland Line Clipping Algorithm:In the algorithm, first of all, it is detected whether line lies inside the screen or it is outside the screen. All lines come under any one of the following categories:
1. Visible: If a line lies within the window, i.e., both endpoints of the line lies within the window. A line is visible and will be displayed as it is. 2. Not Visible: If a line lies outside the window it will be invisible and rejected. Such lines will not display. If any one of the following inequalities is satisfied, then the line is considered invisible. Let A (x1,y2) and B (x2,y2) are endpoints of line. xmin,xmax are coordinates of the window. ymin,ymax are also coordinates of the window. 3. Clipping Case: If the line is neither visible case nor invisible case. It is considered to be clipped case. First of all, the category of a line is found based on nine regions given below. All nine regions are assigned codes. Each code is of 4 bits. If both endpoints of the line have end bits zero, then the line is considered to be visible. 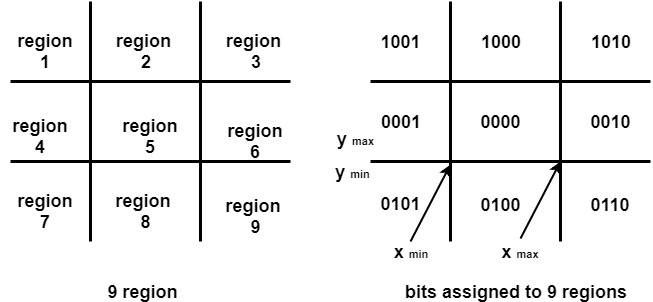
The center area is having the code, 0000, i.e., region 5 is considered a rectangle window. Following figure show lines of various types 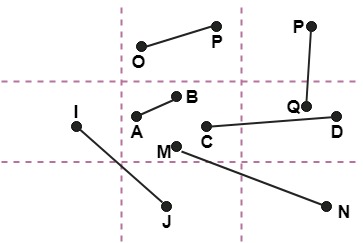
Line AB is the visible case Advantage of Cohen Sutherland Line Clipping:
Algorithm of Cohen Sutherland Line Clipping:Step1:Calculate positions of both endpoints of the line Step2:Perform OR operation on both of these end-points Step3:If the OR operation gives 0000 Step4:If a line is clipped case, find an intersection with boundaries of the window (a) If bit 1 is "1" line intersects with left boundary of rectangle window (b) If bit 2 is "1" line intersect with right boundary (c) If bit 3 is "1" line intersects with bottom boundary (d) If bit 4 is "1" line intersects with the top boundary Example of Cohen-Sutherland Line Clipping Algorithm:Let R be the rectangular window whose lower left-hand corner is at L (-3, 1) and upper right-hand corner is at R (2, 6). Find the region codes for the endpoints in fig: 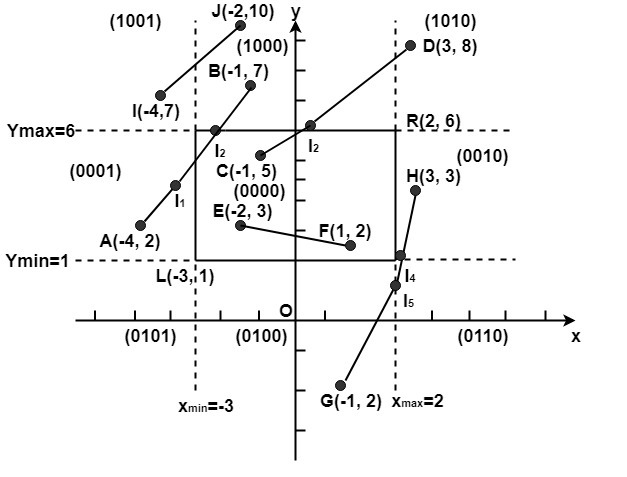
The region code for point (x, y) is set according to the scheme Here 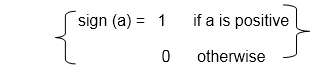
So A (-4, 2)→ 0001 F (1, 2)→ 0000 We place the line segments in their appropriate categories by testing the region codes found in the problem. Category1 (visible): EF since the region code for both endpoints is 0000. Category2 (not visible): IJ since (1001) AND (1000) =1000 (which is not 0000). Category 3 (candidate for clipping): AB since (0001) AND (1000) = 0000, CD since (0000) AND (1010) =0000, and GH. since (0100) AND (0010) =0000. The candidates for clipping are AB, CD, and GH. In clipping AB, the code for A is 0001. To push the 1 to 0, we clip against the boundary line xmin=-3. The resulting intersection point is I1 (-3,3 For clipping CD, we start with D since it is outside the window. Its code is 1010. We push the first 1 to a 0 by clipping against the line ymax=6. The resulting intersection I3 is ( For clipping GH, we can start with either G or H since both are outside the window. The code for G is 0100, and we push the 1 to a 0 by clipping against the line ymin=1.The resulting intersection point is I4 (2 Program to perform Line Clipping using Cohen Sutherland Algorithm:Output: 
Next TopicMidpoint Subdivision Algorithm
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share




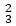 ). We clip (do not display)
). We clip (do not display) 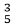 ,6). Thus
,6). Thus 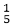 ,1) and its code is 0010. We clip
,1) and its code is 0010. We clip 




