Trignometric Method:The following equation defines an ellipse trigonometrically as shown in fig: x = a * cos (θ) +h and In this method, the value of θ is varied from 0 to 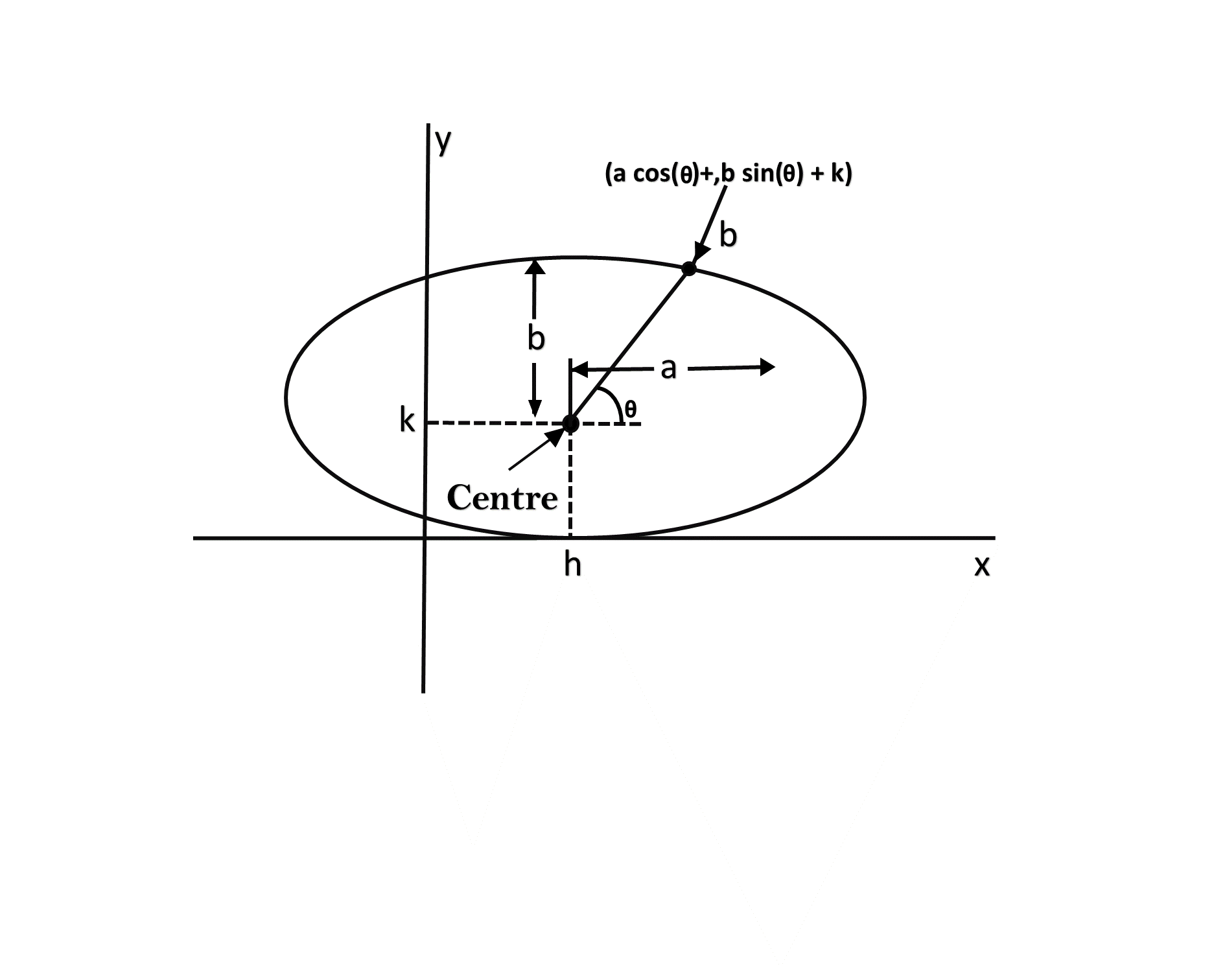
Drawback:
Algorithm:Step1: Start Algorithm Step2: Declare variable x1,y1,aa1,bb1,aa2,bb2,fx,fy,p1,a1,b1 Step3: Initialize x1=0 and y1=b/* values of starting point of circle */ Step4: Calculate aa1=a1*a1 Step5: Initialize fx = 0 Step6: Initialize fy = aa_2* b1 Step7: Calculate the value of p1and round if it is integer Step8:
While (fx < fy)
{
Set pixel (x1,y1)
Increment x i.e., x = x + 1
Calculate fx = fx + bb2
If (p1 < 0)
Calculate p1 = p1 + fx + bb1/
else
{
Decrement y i.e., y = y-1
Calculate fy = fy - 992;
p1=p1 + fx + bb1-fy
}
}
Step9: Setpixel (x1,y1) Step10: Calculate p1=bb1 (x+.5)(x+.5)+aa(y-1)(y-1)-aa1*bb1 Step 11:
While (y1>0)
{
Decrement y i.e., y = y-1
fy=fx-aa2/
if (p1>=0)
p1=p1 - fx + aa1/
else
{
Increment x i.e., x = x + 1
fx= fx+bb_2
p1=p1+fx-fy-aa1
}
}
Set pixel (x1,y1)
Step12: Stop Algorithm Program to draw a circle using Trigonometric method:Output: 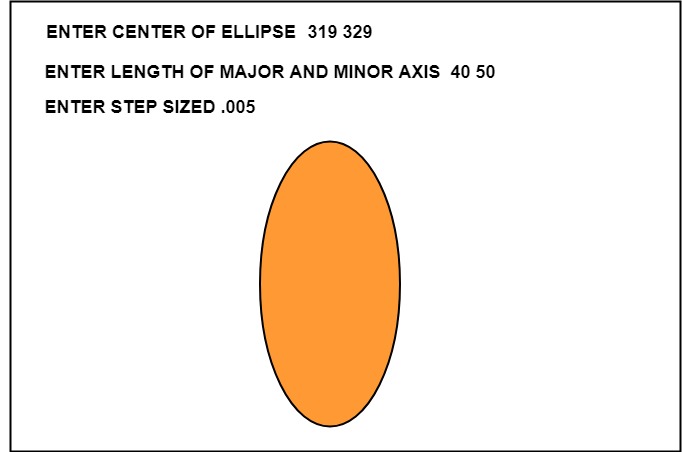
Ellipse Axis Rotation:Since the ellipse shows four-way symmetry, it can easily be rotated. The new equation is found by trading a and b, the values which describe the major and minor axes. When the polynomial method is used, the equations used to describe the ellipse become 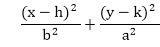
where (h, k) = ellipse center Where (x, y) = current coordinates Assume that you would like to rotate the ellipse through an angle other than 90 degrees. The rotation of the ellipse may be accomplished by rotating the x &y axis α degrees. x = a cos (0) - b sin (0+ ∞) + h y= b (sin 0) + a cos (0+∞) + k 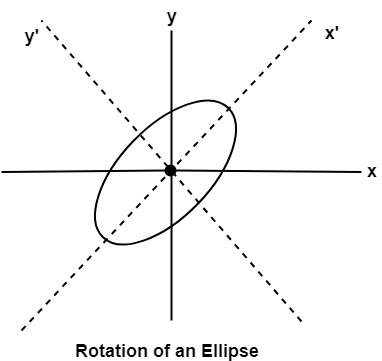
Next TopicMidpoint Ellipse Algorithm
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share





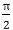 radians. The remaining points are found by symmetry.
radians. The remaining points are found by symmetry.




