Decimal or BCD Adder
The BCD-Adder is used in the computers and the calculators that perform arithmetic operation directly in the decimal number system. The BCD-Adder accepts the binary-coded form of decimal numbers. The Decimal-Adder requires a minimum of nine inputs and five outputs.
Note: The decimal number requires 4 bits to represent in the BCD code, and the circuit must have an input carry and an output carry.
There is the following table used in designing of BCD-Adder.
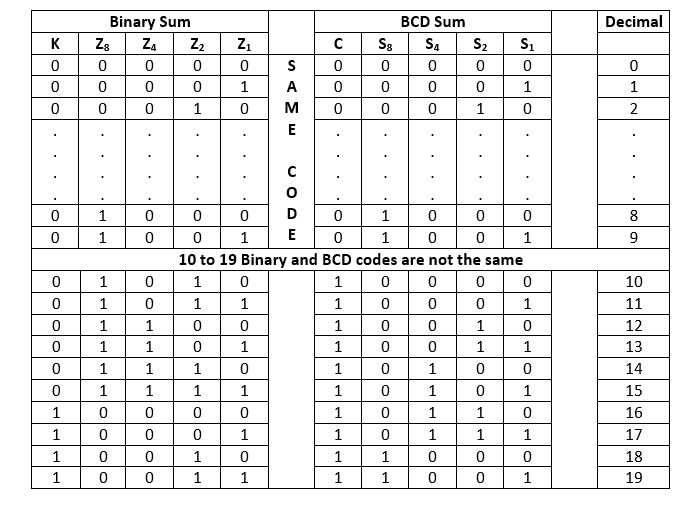
From the above table, it is clear that if the produced sum is between 1 to 9, the Binary and the BCD code is the same. But for 10 to 19 decimal numbers, both the codes are different. In the above table, the binary sum combinations from 10 to 19 give invalid BCD. There are the following points that help the circuit to identify the invalid BCD.
- It is obvious from the table that a correction is needed when the 'Binary Sum' has an output carry K=1.
- The other six combinations from 10 to 15 need correction in which the bit on the Z8 position is 1.
- In the Binary sum of 8 and 9, the bit on the Z8 position is also 1. So, the second step fails, and we need to modify it.
- To distinguish these two numbers, we specify that the bit on the Z4 or Z2 position also needs to be 1 with the bit of Z8
- The condition for a correction and an output carry can be expressed by the Boolean function:
C=K+Z8.Z4+Z8.Z2
Once the circuit found the invalid BCD, the circuit adds the binary number of 6 into the invalid BCD code to make it valid.
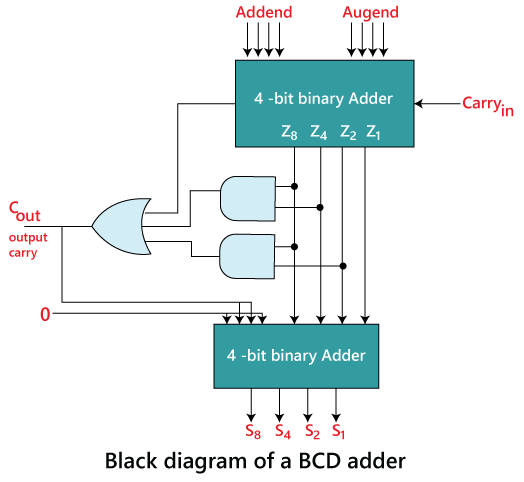
In the above diagram,
- We take a 4-bit Binary-Adder, which takes addend and augend bits as an input with an input carry 'Carry in'.
- The Binary-Adder produces five outputs, i.e., Z8, Z4, Z2, Z1, and an output carry K.
- With the help of the output carry K and Z8, Z4, Z2, Z1 outputs, the logical circuit is designed to identify the Cout
- The Z8, Z4, Z2, and Z1 outputs of the binary adder are passed into the 2nd 4-bit binary adder as an Augend.
- The addend bit of the 2nd 4-bit binary adder is designed in such a way that the 1st and the 4th bit of the addend number are 0 and the 2nd and the 3rd bit are the same as Cout. When the value of Cout is 0, the addend number will be 0000, which produce the same result as the 1st 4-bit binary number. But when the value of the Cout is 1, the addend bit will be 0110, i.e., 6, which adds with the augent to get the valid BCD number.
Example: 1001+1000
- First, add both the numbers using a 4-bit binary adder and pass the input carry to 0.
- The binary adder produced the result 0001 and carried output 'K' 1.
- Then, find the Cout value to identify that the produced BCD is invalid or valid using the expression Cout=K+Z8.Z4+Z8.Z2.
K = 1
Z8 = 0
Z4 = 0
Z2 = 0
Cout = 1+0*0+0*0
Cout = 1+0+0
Cout = 1
- The value of Cout is 1, which expresses that the produced BCD code is invalid. Then, add the output of the 1st 4-bit binary adder with 0110.
= 0001+0110
= 0111
- The BCD is represented by the carry output as:
BCD=Cout Z8 Z4 Z2 Z1=1 0 1 1 1
|


 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now









