Full Subtractor

The Half Subtractor is used to subtract only two numbers. To overcome this problem, a full subtractor was designed. The full subtractor is used to subtract three 1-bit numbers A, B, and C, which are minuend, subtrahend, and borrow, respectively. The full subtractor has three input states and two output states i.e., diff and borrow.

Block diagram

Truth Table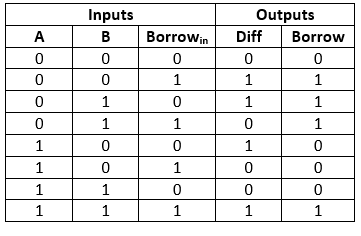

In the above table,

• 'A' and' B' are the input variables. These variables represent the two significant bits that are going to be subtracted.
• 'Borrow_in' is the third input which represents borrow.
• The 'Diff' and 'Borrow' are the output variables that define the output values.
• The eight rows under the input variable designate all possible combinations of 0 and 1 that can occur in these variables.

Note: We can simplify each of the Boolean output functions with the help of the unique map method.

The SOP form can be obtained with the help of K-map as: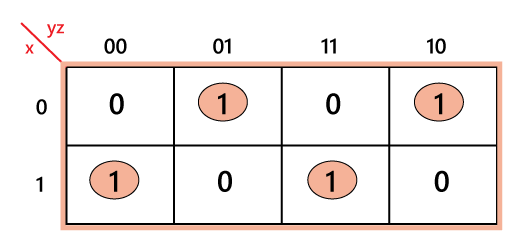

Diff=xy' z'+x' y' z+xyz+x'yz'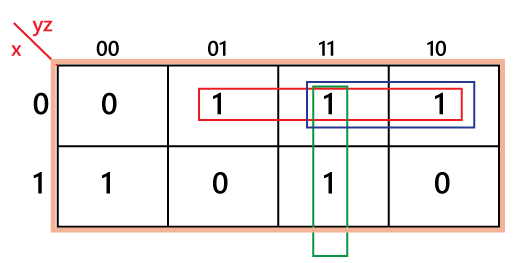

Borrow=x' z+x' y+yz

Construction of Full Subtractor Circuit: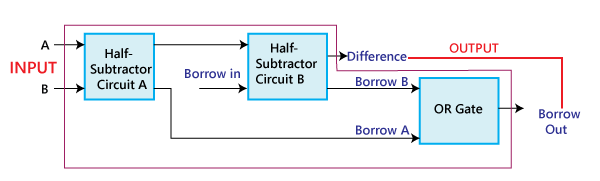

The above block diagram describes the construction of the Full subtractor circuit. In the above circuit, there are two half adder circuits that are combined using the OR gate. The first half subtractor has two single-bit binary inputs A and B. As we know that, the half subtractor produces two outputs, i.e., 'Diff' and 'Borrow'. The 'Diff' output of the first subtractor will be the first input of the second half subtractor, and the 'Borrow' output of the first subtractor will be the second input of the second half subtractor. The second half subtractor will again provide 'Diff' and 'Borrow'. The final outcome of the Full subtractor circuit is the 'Diff' bit. In order to find the final output of the 'Borrow', we provide the 'Borrow' of the first and the second subtractor into the OR gate. The outcome of the OR gate will be the final carry 'Borrow' of full subtractor circuit.

The MSB is represented by the final 'Borrow' bit.

The full subtractor logic circuit can be constructed using the 'AND', 'XOR', and NOT gate with an OR gate.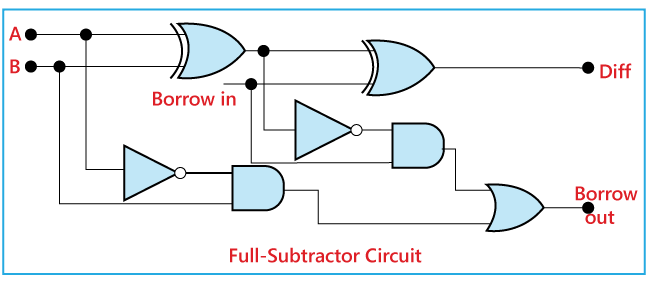

The actual logic circuit of the full subtractor is shown in the above diagram. The full subtractor circuit construction can also be represented in a Boolean expression.

Diff:

• Perform the XOR operation of input A and B.
• Perform the XOR operation of the outcome with 'Borrow'. So, the difference is (A XOR B) XOR 'Borrow_in' which is also represented as:
  (A ⊕ B) ⊕ 'Borrow_in'

Borrow:

• Perform the 'AND' operation of the inverted input A and B.
• Perform the 'XOR' operation of input A and B.
• Perform the 'OR' operations of both the outputs that come from the previous two steps. So the 'Borrow' can be represented as:
  A'.B + (A ⊕ B)'