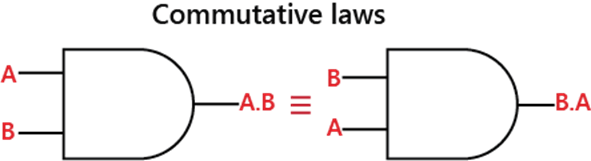
Laws and Rules of Boolean algebraIn simplification of the Boolean expression, the laws and rules of the Boolean algebra play an important role. Before understanding these laws and rules of Boolean algebra, understand the Boolean operations addition and multiplication concept. Boolean AdditionThe addition operation of Boolean algebra is similar to the OR operation. In digital circuits, the OR operation is used to calculate the sum term, without using AND operation. A + B, A + B', A + B + C', and A' + B + + D' are some of the examples of 'sum term'. The value of the sum term is true when one or more than one literals are true and false when all the literals are false. Boolean MultiplicationThe multiplication operation of Boolean algebra is similar to the AND operation. In digital circuits, the AND operation calculates the product, without using OR operation. AB, AB, ABC, and ABCD are some of the examples of the product term. The value of the product term is true when all the literals are true and false when any one of the literal is false. Laws of Boolean algebraThere are the following laws of Boolean algebra: Commutative LawThis law states that no matter in which order we use the variables. It means that the order of variables doesn't matter. In Boolean algebra, the OR and the addition operations are similar. In the below diagram, the OR gate display that the order of the input variables does not matter at all. For two variables, the commutative law of addition is written as:
A+B = B+A

For two variables, the commutative law of multiplication is written as:
A.B = B.A
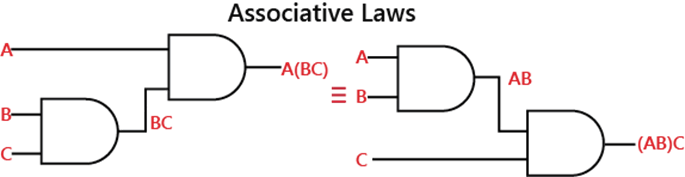
Associative LawThis law states that the operation can be performed in any order when the variables priority is same. As '*' and '/' have same priority. In the below diagram, the associative law is applied to the 2-input OR gate. For three variables, the associative law of addition is written as:
A + (B + C) = (A + B) + C
For three variables, the associative law of multiplication is written as:
A(BC) = (AB)C
According to this law, no matter in what order the variables are grouped when ANDing more than two variables. In the below diagram, the associative law is applied to 2-input AND gate. 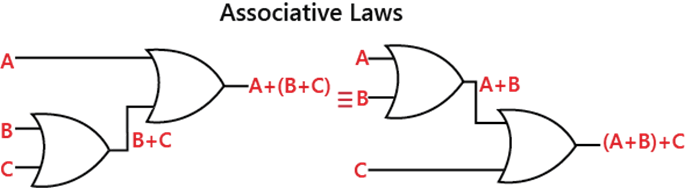
Distributive Law:According to this law, if we perform the OR operation of two or more variables and then perform the AND operation of the result with a single variable, then the result will be similar to performing the AND operation of that single variable with each two or more variable and then perform the OR operation of that product. This law explains the process of factoring. For three variables, the distributive law is written as:
A(B + C) = AB + AC
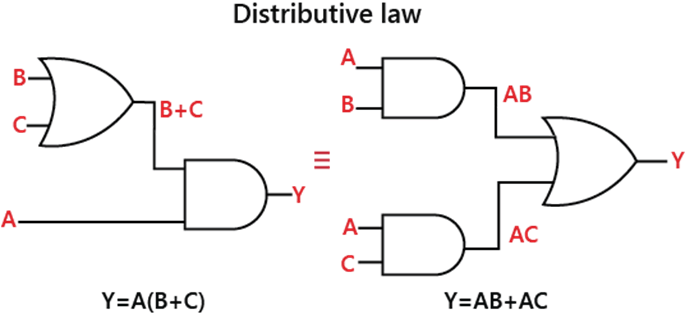
Rules of Boolean algebraThere are the following rules of Boolean algebra, which are mostly used in manipulating and simplifying Boolean expressions. These rules plays an important role in simplifying boolean expressions.
Rule 1: A + 0 = ALet's suppose; we have an input variable A whose value is either 0 or 1. When we perform OR operation with 0, the result will be the same as the input variable. So, if the variable value is 1, then the result will be 1, and if the variable value is 0, then the result will be 0. Diagrammatically, this rule can be defined as: 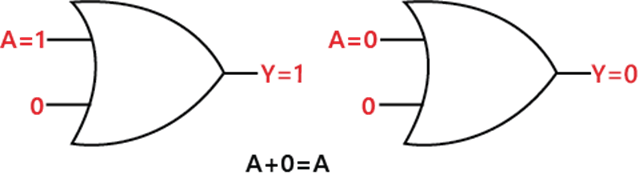
Rule 2: (A + 1) = 1Let's suppose; we have an input variable A whose value is either 0 or 1. When we perform OR operation with 1, the result will always be 1. So, if the variable value is either 1 or 0, then the result will always be 1. Diagrammatically, this rule can be defined as: 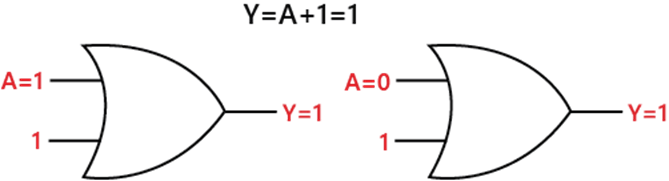
Rule 3: (A.0) = 0Let's suppose; we have an input variable A whose value is either 0 or 1. When we perform the AND operation with 0, the result will always be 0. This rule states that an input variable ANDed with 0 is equal to 0 always. Diagrammatically, this rule can be defined as: 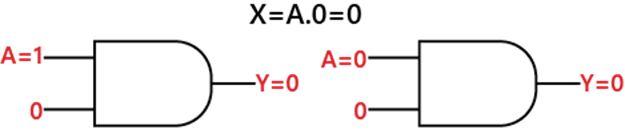
Rule 4: (A.1) = ALet's suppose; we have an input variable A whose value is either 0 or 1. When we perform the AND operation with 1, the result will always be equal to the input variable. This rule states that an input variable ANDed with 1 is equal to the input variable always. Diagrammatically, this rule can be defined as: 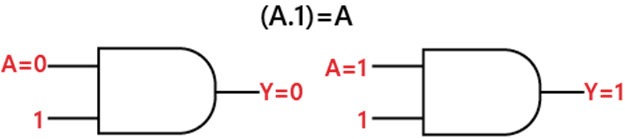
Rule 5: (A + A) = ALet's suppose; we have an input variable A whose value is either 0 or 1. When we perform the OR operation with the same variable, the result will always be equal to the input variable. This rule states an input variable ORed with itself is equal to the input variable always. Diagrammatically, this rule can be defined as: 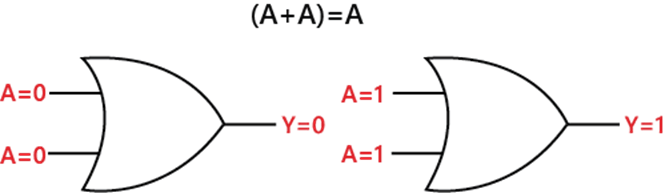
Rule 6: (A + A') = 1Let's suppose; we have an input variable A whose value is either 0 or 1. When we perform the OR operation with the complement of that variable, the result will always be equal to 1. This rule states that a variable ORed with its complement is equal to 1 always. Diagrammatically, this rule can be defined as: 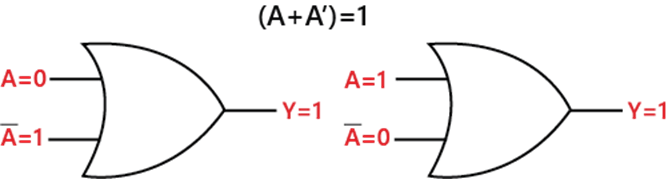
Rule 7: (A.A) = ALet's suppose; we have an input variable A whose value is either 0 or 1. When we perform the AND operation with the same variable, the result will always be equal to that variable only. This rule states that a variable ANDed with itself is equal to the input variable always. Diagrammatically, this rule can be defined as: 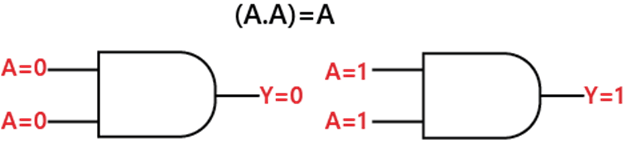
Rule 8: (A.A') = 0Let's suppose; we have an input variable A whose value is either 0 or 1. When we perform the AND operation with the complement of that variable, the result will always be equal to 0. This rule states that a variable ANDed with its complement is equal to 0 always. Diagrammatically, this rule can be defined as: 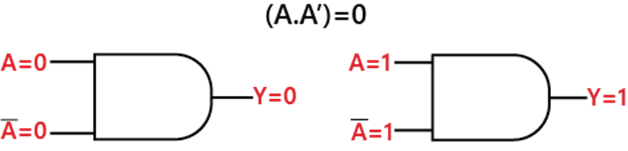
Rule 9: A = (A')'This rule states that if we perform the double complement of the variable, the result will be the same as the original variable. So, when we perform the complement of variable A, then the result will be A'. Further if we again perform the complement of A', we will get A, that is the original variable. 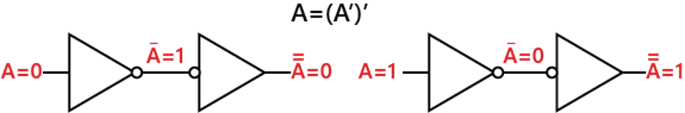
Rule 10: (A + AB) = AWe can prove this rule by using the rule 2, rule 4, and the distributive law as:
A + AB = A(1 + B) Factoring (distributive law)
A + AB = A.1 Rule 2: (1 + B)= 1 A + AB = A Rule 4: A .1 = A 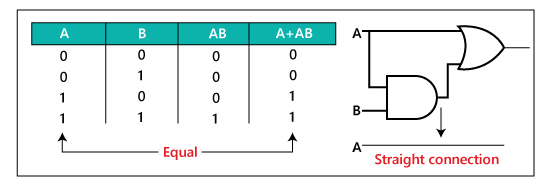
Rule 11: A + AB = A + BWe can prove this rule by using the above rules as:
A + AB = (A + AB)+ AB Rule 10: A = A + AB
A+AB= (AA + AB)+ AB Rule 7: A = AA A+AB=AA +AB +AA +AB Rule 8: adding AA = 0 A+AB= (A + A)(A + B) Factoring A+AB= 1.(A + B) Rule 6: A + A = 1 A+AB=A + B Rule 4: drop the 1 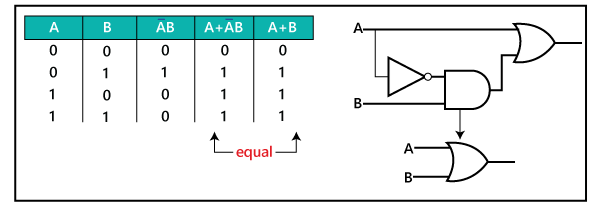
Rule 12: (A + B)(A + C) = A + BCWe can prove this rule by using the above rules as:
(A + B)(A + C)= AA + AC + AB + BC Distributive law
(A + B)(A + C)= A + AC + AB + BC Rule 7: AA = A (A + B)(A + C)= A( 1 + C)+ AB + BC Rule 2: 1 + C = 1 (A + B)(A + C)= A.1 + AB + BC Factoring (distributive law) (A + B)(A + C)= A(1 + B)+ BC Rule 2: 1 + B = 1 (A + B)(A + C)= A.1 + BC Rule 4: A .1 = A (A + B)(A + C)= A + BC 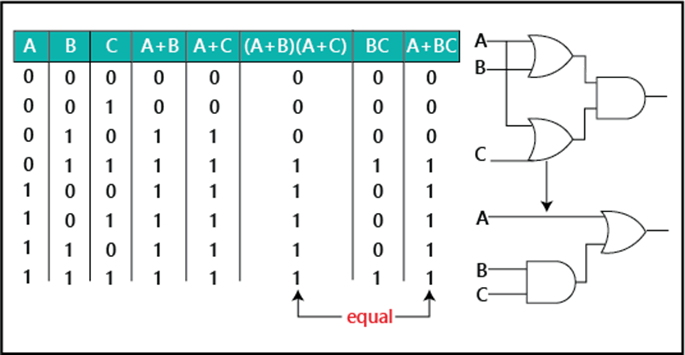
Next TopicLogic Gates
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









