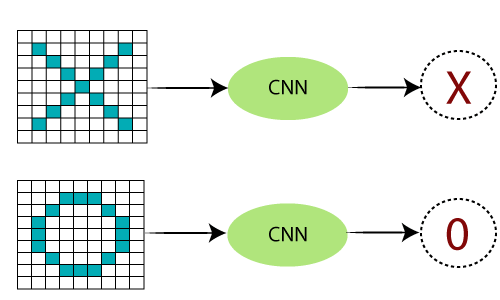
Working of Convolutional Neural NetworkCNN (Convolutional Neural Network or ConvNet) is a type of feed-forward artificial network where the connectivity pattern between its neurons is inspired by the organization of the animal visual cortex. The visual cortex has a small region of cells that are sensitive to specific regions of the visual field. Some individual neuronal cells in our brain respond in the presence of edges of a certain orientation. For example, Some neurons fires when exposed to vertices edges and some when shown horizontal or diagonal edges. CNN utilizes spatial correlations which exist with the input data. Each concurrent layer of the neural network connects some input neurons. This region is called a local receptive field. The local receptive field focuses on hidden neurons. The hidden neuron processes the input data inside the mentioned field, not realizing the changes outside the specific boundary. Working of CNNGenerally, A Convolutional neural network has three layers. And we understand each layer one by one with the help of an example of the classifier. With it can classify an image of an X and O. So, with the case, we will understand all four layers. Convolutional Neural Networks have the following layers:
There are certain trickier cases where X can represent in these four forms as well as the right side, so these are nothing but the effects of the deformed images. Here, there are multiple presentations of X and O's. This makes it tricky for the computer to recognize. But the goal is that if the input signal looks like previous images it has seen before, the "image" reference signal will be convolved with, the input signal. The resulting output signal is then passed on to the next layer. Consider the diagram shown below: 
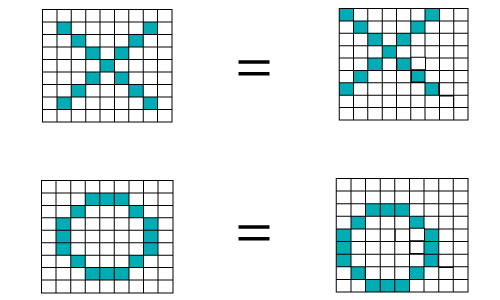
A computer understands an image using numbers at each pixel. In our example, we have considered that a blue pixel will have value 1, and a white pixel will have -1 value. This is as the way we've implemented to differentiate the pixels in a primary binary classification. 
When we use standard techniques to compare these two images, one is a proper image of X, and another is a distorted image of X. We found that the computer is not able to classify the deformed image of X. It is comparing with the proper representation of X. So when we add the pixel values of both of these images, we get something, so a computer is not able to recognize whether it is an X or not. 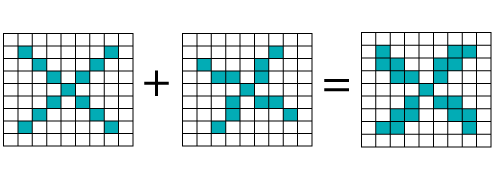
With the help of CNN, we take small patches of our image, so these pieces or patches are known as filters. We were finding rough feature matches in the same position in two pictures. CNN gets better with the similarity between the whole image matching schemes. We have these filters, so consider this first filter this is precisely equal to the feature of the part of the image in the deformed images as well as this is a proper image. CNN compares the piece of the image by section. By finding rough matches, in roughly the same position in two images, CNN gets a lot better at seeing similarity than whole-image matching schemes. 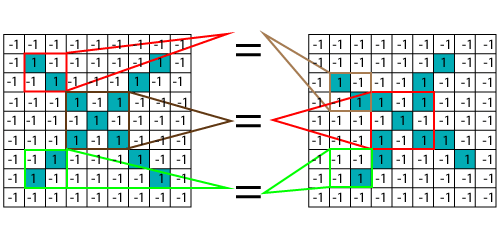
We have three features or filters, as shown below. 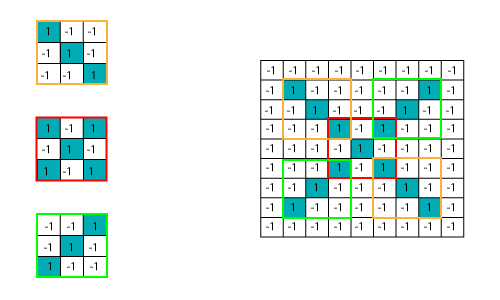
Multiplying the Corresponding Pixel Values 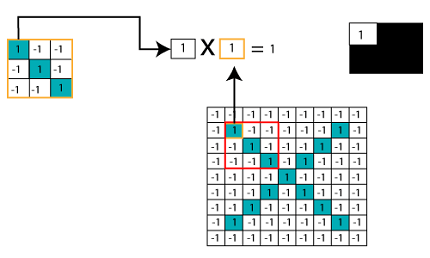 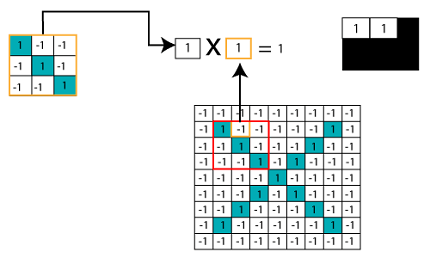
Adding and Dividing by total number of pixels 
Creating a Map to put the value of the filter at the place To keep track of the feature where we create the map and put an amount of filter at that place. 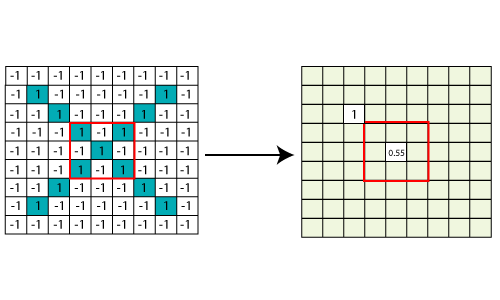
Sliding the Filter throughout the Image Now, using the same functionality and move it to another location and perform the filtering again. 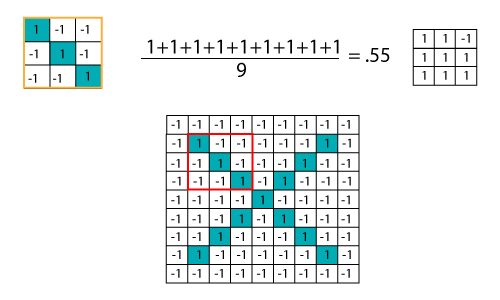
Convolution Layer OutputWe will transfer the features to every other position of the image and will see how the features match that area. Finally, we will get an output as; 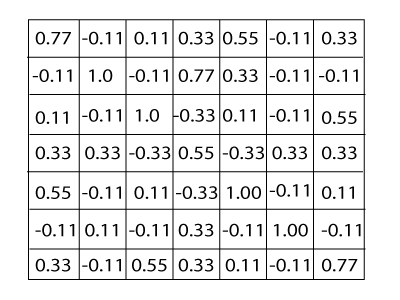
Similarly, we perform the same convolution with every other filter. 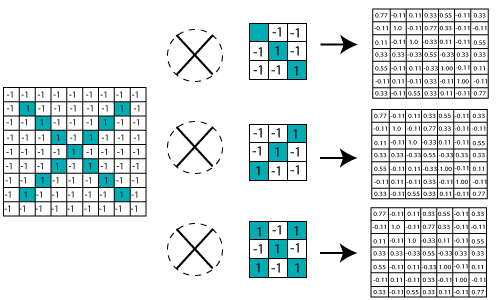
ReLU LayerIn this layer, we remove every negative value from the filtered images and replaces them with zeros. It is happening to avoid the values from adding up to zero. Rectified Linear unit(ReLU) transform functions only activates a node if the input is above a certain quantity. While the data is below zero, the output is zero, but when the information rises above a threshold. It has a linear relationship with the dependent variable. 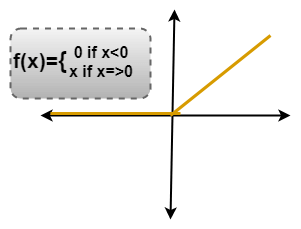
We have considered any simple function with the value as mentioned above. So the function only operates if the dependent variable obtains that value. For example, the following values are obtained. 
Removing the Negative Values 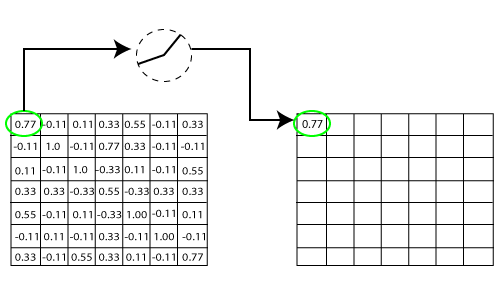
Output for one feature 
Output for all features 
Pooling LayerIn the layer, we shrink the image stack into a smaller size. Pooling is done after passing by the activation layer. We do by implementing the following 4 steps:
Let us understand this with an example. Consider performing pooling with the window size of 2 and stride is 2 as well. Calculating the maximum value in each Window Let's start our first filtered image. In our first Window, the maximum or highest value is 1, so we track that and move the Window two strides. 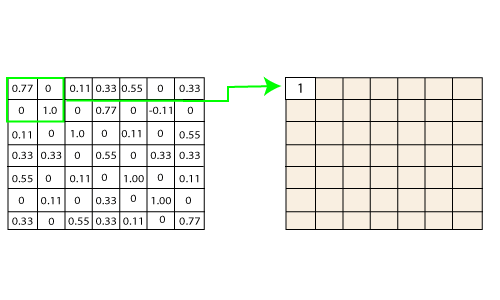
Moving the Window Across the entire image 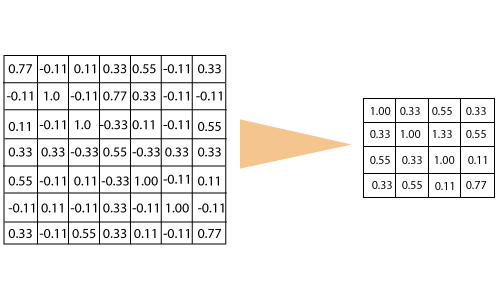
Output after passing through pooling layer 
Stacking up the layersSo that get the time-frame in one picture we are here with a 4×4 matrix from a 7×7 matrix after passing the input through 3 layers - Convolution, ReLU, and Pooling as shown below: 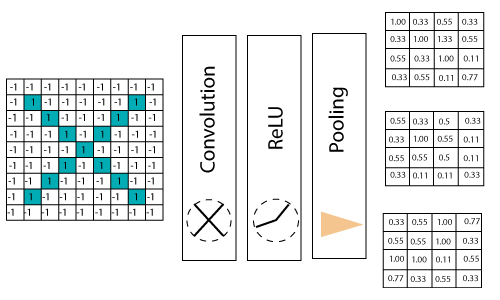
we reduce the image from 4×4 to something lesser?We need to perform 3 operations in the iteration after the first pass. So after the second pass, we arrived at a 2×2 matrix, as shown below: 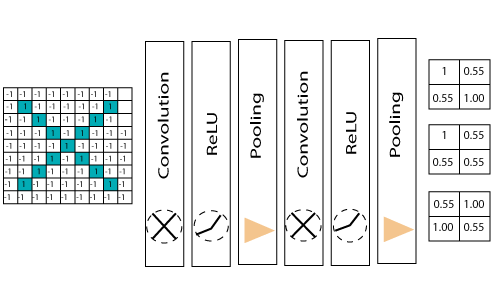
The last layer in the network is fully connected, meaning that neurons of preceding layers are connected to every neuron in subsequent layers. This mimics high-level reasoning where all possible pathways from the input to output are considered. Then, take the shrunk image and put into the single list, so we have got after passing through two layers of convolution relo and pooling and then converting it into a single file or a vector. We take the first Value 1, and then we retake 0.55 we take 0.55 then we retake 1. Then we take 1 then we take 0.55, and then we take 1 then 0.55 and 0.55 then again retake 0.55 take 0.55, 1, 1, and 0.55. So, this is nothing but a vector. The fully connected layer is the last layer, where the classification happens. Here we took our filtered and shrunk images and put them into one single list as shown below. 
OutputWhen we feed in, 'X' and '0'. Then there will be some element in the vector that will be high. Consider the image below, as we can see for 'X' there are different top elements, and similarly, for 'O' we have various high elements. There are specific values in my list, which were high, and if we repeat the entire process which we have discussed for the different individual costs. Which will be higher, so for an X we have 1st, 4th, 5th, 10th, and the 11th element of vector values are higher. And for O we have 2nd, 3rd, 9th and 12th element vector which are higher. We know now if we have an input image which has a 1st, 4th, 5th, 10th, and 11th element vector values high. We can classify it as X similarly if our input image has a list which has the 2nd 3rd 9th and 12th element vector values are high so that we can organize it 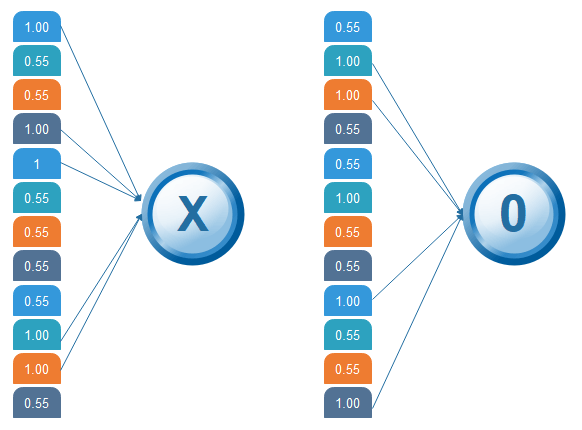
Then the 1st, 4th, 5th, 10th, and 11th values are high, and we can classify the image as 'x.' The concept is similar for other alphabets as well - when certain values are arranged the way they are, they can be mapped to an actual letter or a number which we require Comparing the Input Vector with XAfter the training is done the entire process for both 'X' and 'O.' Then, we got this 12 element vector it has 0.9, 0.65 all these values then now how do we classify it whether it is X or O. We will compare it with the list of X and O so we have got the file in the previous slide if we notice we have got two different lists for X and O. We are comparing this new input image list that we have arrived with the X and O. First let us compare that with X now as well for X there are certain values which will be higher and nothing but 1st 4th 5th 10th and 11th value. So, we are going to sum them, and we have got 5= 1+ 1+ 1+ 1+1 times 1 we got 5, and we are going to sum the corresponding values of our image vector. So the 1st value is 0.9 then the 4th value is 0.87 5th value is 0.96, and 10th value is 0.89, and 11th value is 0.94 so after doing the sum of these values have got 4.56 and divide this by 5 we got 0.9. 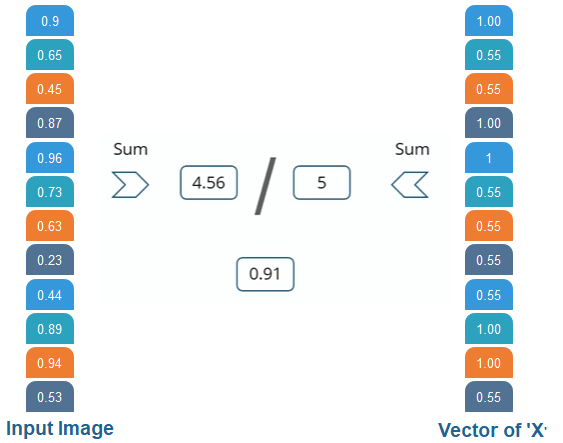
We are comparing the input vector with 0. And for X then we are doing the same process for O we have notice 2nd 3rd 9th, and 12th element vector values are high. So when we sum these values, we get 4 and when we do the sum of the corresponding values of our input image. We have got 2.07 and when we divide that by 4 we got 0.51. 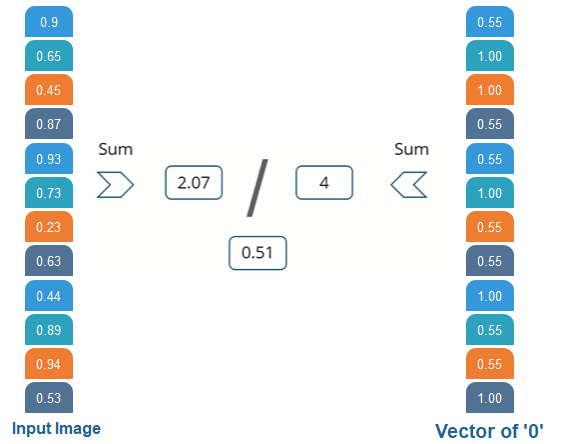
Result Now, we notice that 0.91 is the higher value compared to 0.5 so we have compared our input image with the values of X we got a higher value then the value which we have got after comparing the input image with the values of 4. So the input image is classified as X. 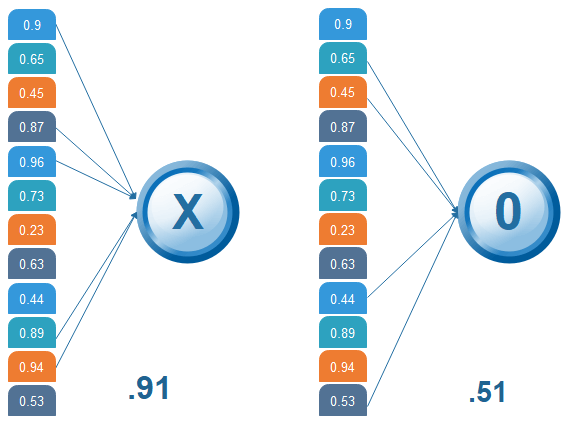
CNN Use CaseSteps: 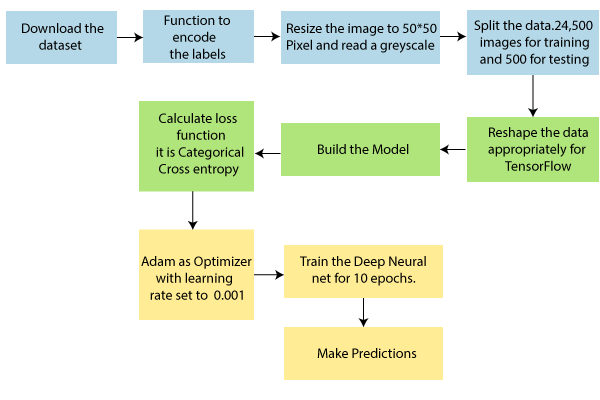
Here, we are going to train our model on different types of dog and cat images, and once the training is done. We are going to provide it will classify whether the input is of a dog or a cat. 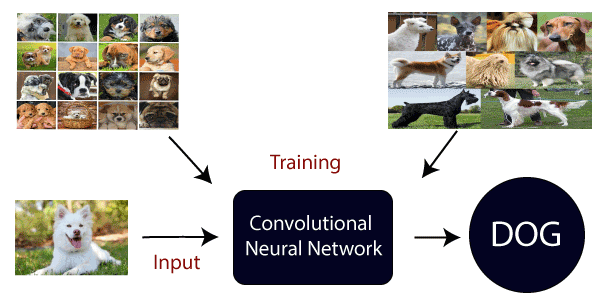
Next TopicTraining of CNN
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










