Aptitude Pipes and Cisterns Test Paper 311) A can fill a tank in 8 hours, B can fill the same in 12 hours, and C can fill the tank in 24 hours. If they are open at 2 am, 3 am, and 4am respectively, then at what time the tank will be completely fill?
The correct answer is C. Answer with explanation: ATQ, At 2am: A starts and fill the tank in 8 hours. Let the capacity of the tank = LCM of (A's, B's, and C's time) Now, A's one hour work = capacity of the tank/ time taken by A. ATQ, between 2am to 3am, only A works = 3 unit To complete the 16 unit work it requires 16/6 = 2[2/3], or 2:40min 12) Two pipes A and B individually can fill a tank in 15 hours, and 12 hours respectively, and C can empty the full tank in 4 hour. If all three pipes are open at 8, 9, and 11 am respectively. At what time tank will be completely empty?
The correct answer is A. Answer with explanation: ATQ, At 8am: A starts and fill the tank in 15 hours. Let the capacity of the tank = LCM of (A's, B's, and C's time)
Now, LCM of 15, 12, and 4 is 60. Now, A's one hour work = capacity of the tank/ time taken by A. ATQ, between 8am to 9am, only A works = 4 units Now, we have to empty the 22 unit water that is stored till 11 am That means the water that is stored till 11 am will be empty in 3hour: 40min So, the time which requires to empty the tank is 11 hour+3 hour+40min = 2:40pm 8) A tank has two pipes. The first pipe can fill it in 45 minutes and the second can empty it in 1 hour. In what time will the empty tank be filled if the pipes be opened one at a time in alternate minutes?
The correct answer is (D) Answer with explanation: Let pipe A can fill a tank in 45 minutes Now, take LCM of A and B to find the capacity of the tank LCM of A (45) and B (60) = 180 Now, 1 minute work of A = 180/45 = 4 units Here ?ve indicates empty tank per minute Now, 176 units will be filled in 176*2 = 352 minutes. Now, the remaining 4 litres will be filled in next 1 minute Therefore, the time taken to fill the tank = 5 hrs + 53 min. 14) A cylindrical tank of diameter 25 cm is full of water. If 11 litres of water is drawn off, the water level in the tank will drop by (use π =22/7).
The correct answer is D. Answer with explanation: Volume of cylinder = π r2 h π r2 h = 11 litres = 11000 cm3 Or h = h = Therefore, the water level in the will be drop by 222/5 cm 15) Two pipes can separately fill a tank in 20 hrs and 30 hrs respectively. Both the pipes are opened to fill the tank but when the tank is
The correct answer is D. Answer with explanation: Let pipe A can fill a tank in 20 hours Now, take LCM of A and B to find the capacity of the tank LCM of A (20) and B (30) = 60 litres Now, A can fill the tank in one hour = 60/20 = 3 litres/hr. If (A+B) both open together then the tank will be filled in 60/ (2+3) = 12 hours. If both pipes open together then to fill 1/3 part of the tank they requires 12/3 = 4 hours Or, in the 4 hours, A+B together will fill 4* 5 = 20 litres. ATQ, (A+B) can fill the tank per hour = 5 litres, but (1/3) of 5 flows out by leakThat means 5/3 litres flow out per hour. Now, total inlet per hour = 5- Aptitude Pipes and Cisterns Test Paper 1 Aptitude Pipes and Cisterns Test Paper 2 Pipes and Cisterns Concepts
Next TopicAptitude Profit and Loss Test Paper 1
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share





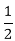 cm
cm 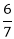 cm
cm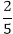 cm
cm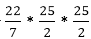 = 11000 cm3
= 11000 cm3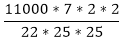
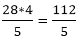 = 22
= 22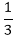 full, a leak develops in the tank through which
full, a leak develops in the tank through which 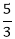 = 10/3 litres
= 10/3 litres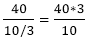 = 12 hours
= 12 hours




