|
1) In what ways the letters of the word "RUMOUR" can be arranged?
Answer: D Answer with the explanation: The word RUMOUR consists of 6 words in which R and U are repeated twice. Hence, 180 words can be formed by arranging the word RUMOUR. 2) In what ways the letters of the word "PUZZLE" can be arranged to form the different new words so that the vowels always come together?
Answer: D Answer with the explanation: The word PUZZLE has 6 different letters. As per the question, the vowels should always come together. Note: we know that 0! = 1Now, the vowels UE can be arranged in 2 different ways, i.e., 2P2 = 2! = 2*1 = 2 ways Hence, the new words, which can be formed after rearranging the letters = 120 *2 = 240 As we known z is occurring twice in the word ‘PUZZLE’ so we will divide the 240 by 2. So, the no. of permutation will be = 240/2 = 120 3) In what ways can a group of 6 boys and 2 girls be made out of the total of 7 boys and 3 girls?
Answer: C Answer with the explanation: We know that nCr = nC(n-r) The combination of 6 boys out of 7 and 2 girls out of 3 can be represented as 7C6 + 3C2 Hence, in 21 ways the group of 6 boys and 2 girls can be made. 4) Out of a group of 7 boys and 6 girls, five boys are selected to form a team so that at least 3 boys are there on the team. In how many ways can it be done?
Answer: C Answer with the explanation: We may have 5 men only, 4 men and 1 woman, and 3 men and 2 women in the committee. So, the combination will be as we know that nCr= So, (7C3 * 6C2) + (7C4 * 6C1) + (7C5) Or, 525 +210+21 = 756 So, there are 756 ways to form a committee. 5) A box contains 2 red balls, 3 black balls, and 4 white balls. Find the number of ways by which 3 balls can be drawn from the box in which at least 1 black ball should be present.
Answer: A Answer with the explanation: The possible combination could be (1 black ball and 2 non-black balls), (2 black balls and 1 non- black ball), and (only 3 black balls). Therefore the required number of combinations = (3C1 * 6C2) + (3C2 * 6C1) + (3C3) Permutation and Combination Test Paper 2 Permutation and Combination Concepts
Next TopicPermutation and Combination Test Paper 2
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share




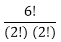
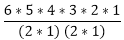 = 180
= 180 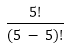 =
= 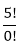 = 5! = 5*4*3*2*1 = 120 ways.
= 5! = 5*4*3*2*1 = 120 ways.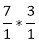 = 21
= 21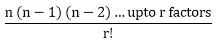
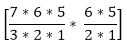 +
+ 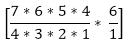 +
+ 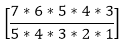
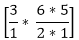 +
+ 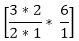 +
+ 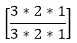 = 45+18+1 = 64
= 45+18+1 = 64




