Permutation and Combination Concepts and FormulasPoints to Remember:1) Factorial: The factorial can be defined as the product of the number (for which we have to find factorial) by its successor till it reaches to one. We can write it as, n! (Factorial of n) = n (n-1) (n-2)....1 For example: The factorial of 3: 3! = 3*2*1 = 6 Note: The factorial of zero (0) is always 1 because an empty set can arrange in one way only.2) Permutation: It refers to the number of ways a particular set can be arranged, where order of the arrangement matters. A combination lock can be called a permutation lock. For example: i) Let we have three letters a, b, and c and we have to arrange two letters at a time. So, in this case, the permutations of the two letters = ab, ba, bc, cb, ac, and ca. ii) If we have to arrange all letters (a,b,c) simultaneously, the permutation would be: abc, acb, bac, bca, cab, and cba. Formula for calculating number of possible permutations of r things, from a set of n at a time is as follows: For example: i. 8P3 = ii. 7P5 iv. The number of permutations or arrangements of all n things at a time = n! (Factorial of n). 3) Combinations: It refers to the number of ways a particular set can be arranged, where order of the arrangement does not matter which means for a combination of the n number of things there may be different orders. Formula for calculating the possible combination for r things, from a set of n objects at a time is as follows: nCr = Note:i) nCn = 1 ii) nC0 = 1 iii) nCr = nC(n-r) For examples: i. 8C3 = Or, 8C3 = 8C(8-3) = 8C5 = ii. 7C5 = 7C(7-5) = 7C2 = Note:
Note: xy and yx are same in the combination.
Permutation and Combination Test Paper 1 Permutation and Combination Test Paper 2
Next TopicPermutation and Combination Test Paper 1
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share





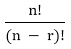
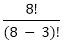 =
= 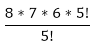 = (8*7*6) = 336
= (8*7*6) = 336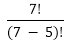 =
= 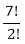 =
= 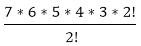 = 2520
= 2520 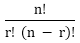 =
= 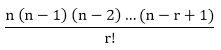
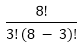 =
= 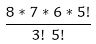 =
= 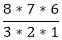 = (8*7) = 56
= (8*7) = 56 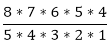 = 8*7 = 56
= 8*7 = 56 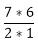 = 21
= 21




