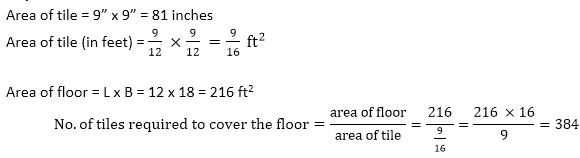Area Aptitude Test Paper 416) The difference between the length and the perimeter of a rectangle is 100 cms. What is the breadth of the rectangle?
Answer: D Explanation: Let the length of the rectangle be 'x' and breadth of the rectangle be 'y' According to the question: 2(x + y) - x = 100 2x + 2y - x = 100 x + 2y = 100 From this we cannot find 'y' (breadth), so the given data is inadequate. 17) The sides of a rhombus are 10 cm in length, and one diagonal is 16 cm. The area of the rhombus is
Answer: A Explanation: When d1 and d2 are the diagonals of rhombus then,
Squaring both sides 202 = 162 + d22 400 = 256 + d22 d22 = 400 - 256 d2 = √144 d2 = 12 Area of rhombus =1/2( d1 × d2 ) =1/2 ( 16 × 12 )=96 cm2 18) If each side of the square is increased by 50%, what will be the ratio between the new area and the original area of the square?
Answer: B Explanation:
19) The sides of a rectangular field are in the ratio 3: 4 and its area is 7500 m2. What is the cost of fencing it at 25 paise per meter?
Answer: A Explanation: Ratio between the sides of rectangle = 3: 4 Let the ratio constant be x then, Length = 3x and breadth = 4x Area = L x B 7500=3x × 4x=12x2 x=25 Length = 3 x 25 = 75 m, and Breadth = 4 x 25 = 100 m Perimeter = 2(75 + 100) = 2 x 175 = 350 m Cost of fencing 1 meter = 25 paise Cost of fencing 350 m = 350 x 25 = 8750 paise In rupees: Rs. 87.50 20) If the size of a tile is 9" by 9", how many tiles are required to cover a 12 ft. wide and 18 ft. long floor?
Answer: B Explanation:
Area Aptitude Test Paper 1 Area Aptitude Test Paper 2 Area Aptitude Test Paper 3 Area Aptitude Test Paper 5 Area Aptitude Test Paper 6 Area Aptitude Test Paper 7 Area Aptitude Test Paper 8 Area Concepts
Next TopicArea Aptitude Test Paper 5
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share





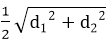
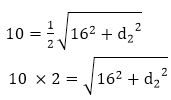
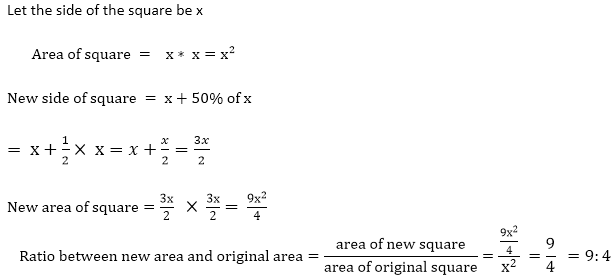
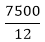 = x2=625
= x2=625