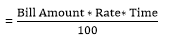Aptitude True Discount and Banker's Discount Concepts and Formulas

Points to Remember:

Present Value: The money to be paid before the due date to clear off debt is called present worth.

True Discount: The difference between the amount due and the present value or worth of the amount is called the true discount. In other words, it is the interest on the present worth.

Banker's Discount: It is the simple interest on the face value or amount due for the period from the date on which the bill was discounted till the legally due date or for the unexpired time.

Concept:

Suppose a merchant A buys goods worth of face value Rs. 2000 (interest of one year included) from another merchant B at a credit of say 12 months or one year. The B prepares a bill called the bill of exchange, which is also known as Hundi. The merchant A signs this bill that allows B to withdraw the amount from his bank account after the specified duration of 12 months.

Let the market interest rate is 5%. The date exactly after the 12 months is called the nominal due date. Furthermore, 3 days grace period is also added to this date of expiry to arrive at a date called legally due date. For example, if 5 April 2008 is the nominally due date, 8 April 2008 will be the legally due date. The amount Rs. 2000 is called the face value. So, according to the bill, the B will receive a face value of Rs. 2000 after twelve months.

Suppose after 6 months, B needs money immediately and cannot wait till due date. In this case, B can approach a bank or broker to pay him money against the bill. In this situation, the money paid by the banker will be less than the face value of the bill.

Let the bill is presented to the banker after six months, the banker will deduct the interest on the face value for the remaining period of six months and this interest is called the Banker's Discount (B.D) or Commercial Discount.

The interest on the bill value (face value) is called the banker's discount and the difference between the banker's discount and true discount (T.D) is called banker's gain (B.G).

Banker's gain = Banker's discount - True discount

B.G. = Interest on the sum due for the unexpired time - Interest no present worth for the unexpired time

= Interest on (sum due - present worth)
= Interest on true discount
The present value of the bill is calculated as follows:
PV * (1+r*T) = FV
PV = present value
r = rate of interest
t = time

So, true discount = Face value - Present value = 2000 - 1951.23 = 48.77

The true discount is the difference between the sum due at the end of the given time and its present worth. So, in the above example, true discount = Face value (sum due) - Present value = 2000 - 1951.23 = 48.77

In other words, the true discount is the simple interest on the present value or worth for the unexpired time. In other words, the present value or present worth of a sum of money due at the end of a specified time is that sum which will amount to the sum due with its interest for the given time at the given rate.

So, if the bank pays Rs. 1951.23 (present worth) to B in exchange for the bill, the bank would not make a profit from this deal. So, the bank does not use true discount but uses another formula to calculate the discount called Banker's Discount.

Banker's Discount: It is the simple interest on the face value (Rs. 2000) of the debt for the time period from the date on which the bill is discontinued to the legally due date, which is six months (unexpired time) in this example. The banker deducts the interest on the face value for the unexpired time.

Banker's Discount = FV * r * t = 2000 * 0.05 * (�) = 50

So, instead of discounting true discount, the Banker discounts the banker's discount from the face value and pays out Rs. 2000 - 50 = Rs.1950

So, Banker's gain = Present Value of the Note - Actual Payout = 1.23
                               = (Face Value - True Discount) - (Face Value - Banker's Discount)

B.G. = Banker's discount - True Discount = 1.23

Formulae:

Let the rate of interest = R% per annum
Time = T years

Banker's Discount (B.D) = S.I (simple interest) on bill for unexpired time

Example 2:

Suppose a merchant has to pay Rs. 164 after 4 years and the rate of interest is 16% per annum. It shows Rs. 100 will amount to Rs. 164 in 4 years. So, a payment of Rs. 164 will clear off the debt of Rs. 164 due 4 years hence.

AS per the above example:
Sum due = Rs. 164 due 4 years hence:
Present Worth (P.W.) = Rs. 100
So, true discount (T.D) = 164 - 100
                                      = 64

We define: T.D. = Interest on P.W so, the Amount Due = P.W + T.D.

Note: If the date of the bill is not given, grace days are not required to be added.