Aptitude Time and Work Test Paper 311) A can do a piece of work in 6 days working 8 hours a day. B can do the same work in 4 days working 6 hours a day. If they work together 8 hours a day, in how many days they will do this work?
The Correct answer is (C) Explanation: A can complete the work in, 6 x 8 = 48 hour B can complete the same work in = 4 x 6 = 24 hours A's one hour work = B's one hour work = (A +B)'s one hour work = They will complete So, the entire work will be completed in 1 ∗ 144 = 144 hours Both work 8 hours a day so the number of days required to complete the work = 12) A can finish a work in 6 days and B can finish the same work in 8 days. A and B charge Rs. 2800 for the work. If with the help of C they complete the work in 3 days, how much they will pay to C?
The Correct answer is (A) Explanation: A's one hour work = 1 B's one hour work = 1 (A +B)'s one hour work = 1 + 1 = 7 (A+B+C)'s one day work = 1 Therefore, C's one day work = 1 - 7 = 1 The ratio of A, B and C's wages will be equal to the ratio of work done by them in one day. A's wages: B's wages: C's wages = 1 : 1 : 1 C's share of three days = 3 * C's share for one day = 3 ∗ (1 ∗ 2800) = 35024 13) 5 men undertook a piece of work and finished half the work in 18 days if two men drop out, in how many days the remaining work will be completed?
The Correct answer is (A) Explanation: 5 men completed half of the work in 18 days so the entire work will be completed in 36 days. 5 men' one day work will be = One man's one day work = Two men drop out, so the three men have to complete the remaining work. Three men's one day work will be =
Therefore, the remaining 14) If 5 workers can paint a house in 9 days, in how many days 3 workers can complete the same task?
The Correct answer is (C) Explanation: Using formula: M1D1W2 =M2D2W1 We have = 5∗9∗W2 = 3∗D2∗W1 W2 = W1 as the task is the same in both the cases, so the amount of work to be done would be the same. Therefore, we have 5 ∗ 9 = 3 ∗ D2 45 = 3∗ D2 D2 = 45 = 15days 15) A group of workers undertakes a task. They can complete the task in 30 days. If 5 of them did not turn for the work and the remaining workers complete the task in 40 days, find the original number of workers.
The Correct answer is (D) Explanation: Let the original number of workers = X X workers can complete the work in 30 days. And (X - 50) complete the same task in 40 days. Apply formula: M1D1W2 =M2D2W1 W1=W2 as the task is the same in both the cases. Therefore, X * 30 = (X - 5) * 40 30 X = 40X - 200 200 = 40X -30X 200 = 10 X X = 200 = 20days Aptitude Time and Work Test Paper 1 Aptitude Time and Work Test Paper 2 Aptitude Time and Work Test Paper 4 Aptitude Time and Work Test Paper 5 Aptitude Time and Work Test Paper 6 Aptitude Time and Work Test Paper 7 Aptitude Time and Work Test Paper 8 Aptitude Time and Work Test Paper 9 Time and Work Concepts
Next TopicTime and Work Test Paper 4
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share





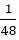
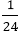
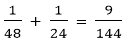
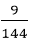
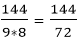 = 2 days
= 2 days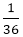
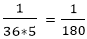
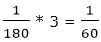
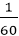 part of the work is completed by three men in one day
part of the work is completed by three men in one day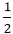 part of the work will be completed in
part of the work will be completed in 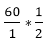 = 30 Days.
= 30 Days.




