Basic Execution Time ModelThis model was established by J.D. Musa in 1979, and it is based on execution time. The basic execution model is the most popular and generally used reliability growth model, mainly because:
The basic execution model determines failure behavior initially using execution time. Execution time may later be converted in calendar time. The failure behavior is a nonhomogeneous Poisson process, which means the associated probability distribution is a Poisson process whose characteristics vary in time. It is equivalent to the M-O logarithmic Poisson execution time model, with different mean value function. The mean value function, in this case, is based on an exponential distribution. Variables involved in the Basic Execution Model: Failure intensity (λ): number of failures per time unit. Execution time (τ): time since the program is running. Mean failures experienced (μ): mean failures experienced in a time interval. In the basic execution model, the mean failures experienced μ is expressed in terms of the execution time (τ) as 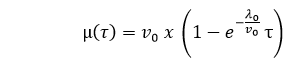
Where -λ0: stands for the initial failure intensity at the start of the execution. -v0: stands for the total number of failures occurring over an infinite time period; it corresponds to the expected number of failures to be observed eventually. The failure intensity expressed as a function of the execution time is given by 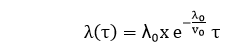
It is based on the above formula. The failure intensity λ is expressed in terms of μ as: 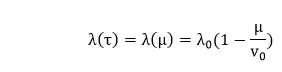
Where λ0: Initial v0: Number of failures experienced, if a program is executed for an infinite time period. μ: Average or expected number of failures experienced at a given period of time. τ: Execution time. 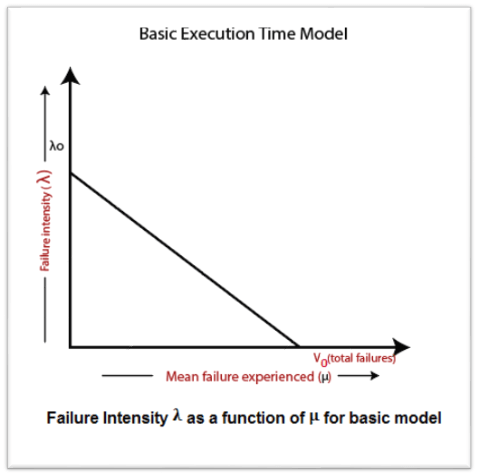
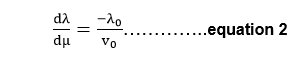
For a derivation of this relationship, equation 1 can be written as: 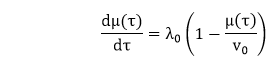
The above equation can be solved for λ(τ) and result in: 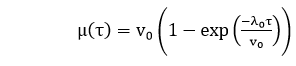
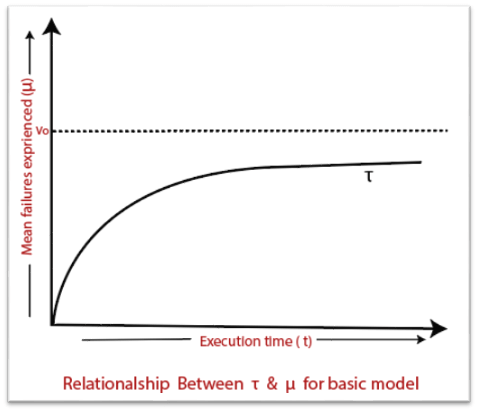
The failure intensity as a function of execution time is shown in fig: 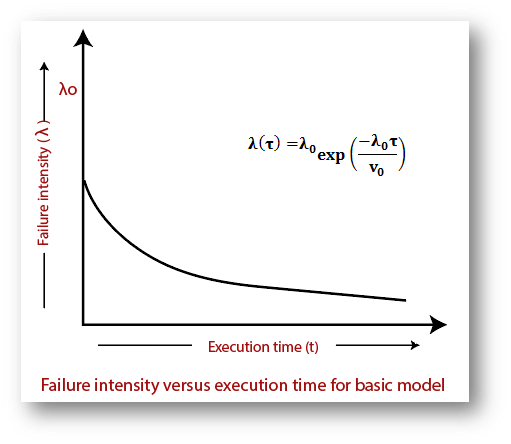
Based on the above expressions, given some failure intensity objective, one can compute the expected number of failures ∆λ and the additional execution time ∆τ required to reach that objective. 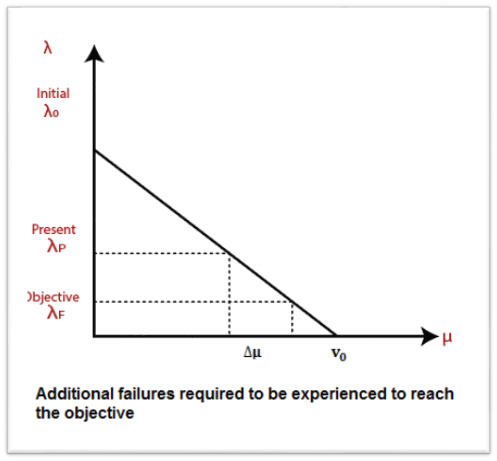
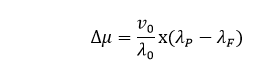
Where λ0: Initial failure Intensity λP: Present failure Intensity λF: Failure of Intensity objective ∆μ: Expected number of additional failures to be experienced to reach failure intensity objectives. 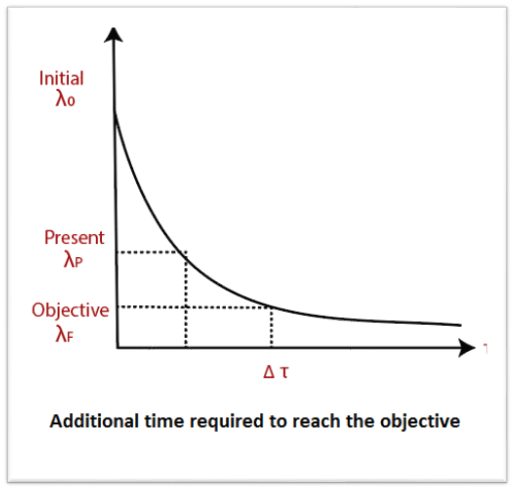
This can be derived in mathematical form: 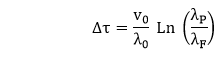
Example: Assume that a program will experience 200 failures in infinite time. It has now experienced 100. The initial failure intensity was 20
Use the basic execution time model for the above-mentioned calculations. Solution: 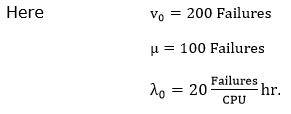
(1)Current Failure Intensity: 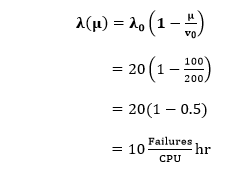
(2)Decrement of failure Intensity per failure can be calculated as: 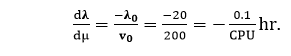
(3)(a) Failures experienced & Failure Intensity after 20 CPU hr. 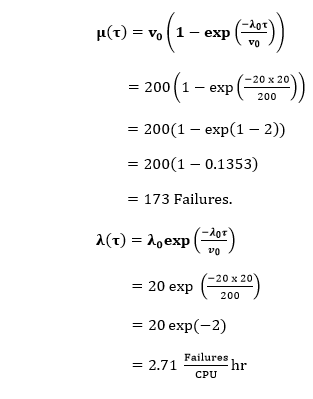
(b)Failures experienced & Failure Intensity after 100 CPU hr. 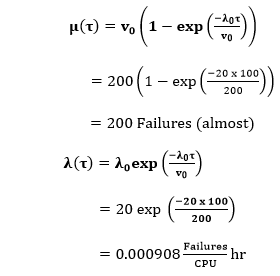
4. Additional failures (∆μ) required to reach the failure intensity objectives of 5 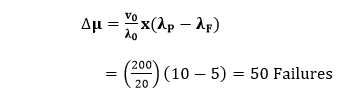
The additional execution time required to reach the failure intensity objectives of 5 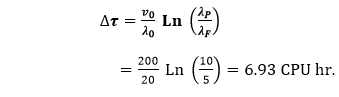
Next TopicGoel-Okumoto (GO) Model
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share




 hr. Determine the current failure intensity.
hr. Determine the current failure intensity.




