Boston Housing Kaggle Challenge with Linear RegressionBoston Housing DataThe database is kept by Carnegie Mellon University and was obtained from the StatLib library. The housing costs in Boston are the subject of this dataset. There are 506 instances and 13 features in the supplied dataset. The following table shows the summary of the dataset, which was derived from the citation below. Our goal is to develop a model with this data utilizing linear regression to forecast the price of homes. The following columns are present in the data:
P.S. I am still learning how and where to interpret the graphs; this is my first analysis. Code: Output: 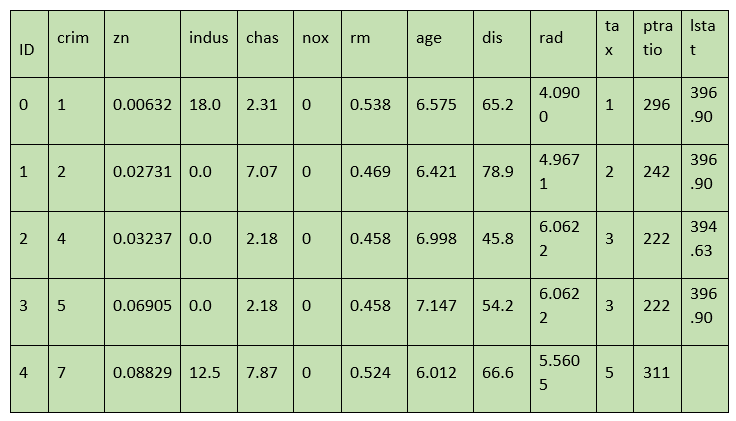
Input: Output: (506, 13 ) Input: Output: Array[ 'crim', 'zn', 'indus' ,'chas', 'nox' , 'rm', 'age', 'dis', 'rad', 'tax', 'ptratio' ] Data conversion to nd-array to info frame and feature names addition Input: Output: 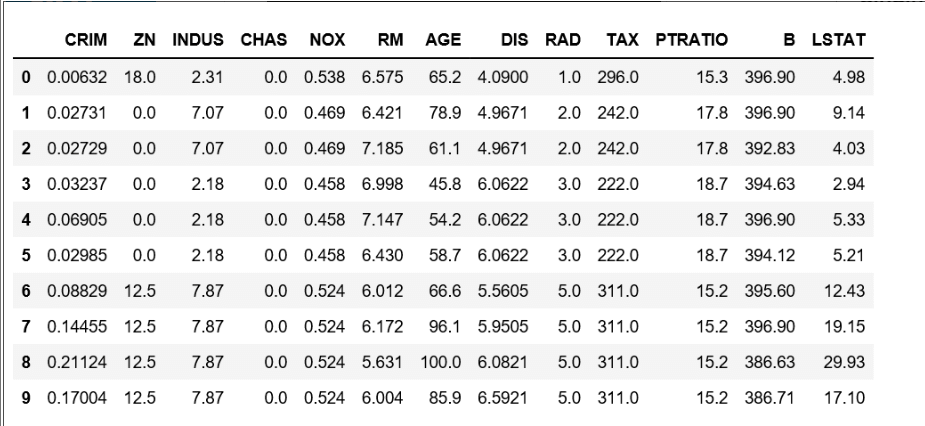
Input: Output: (506, ) Input: Output: 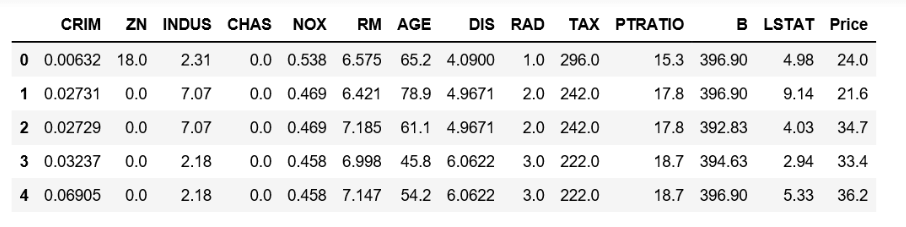
Obtaining input and output data, then dividing the data into training and testing datasets. Output: atrain shape flow: (403, 13) atest shape flow: (102, 13) btrain shape flow: (404, ) btest shape flow: (102, ) utilising the dataset and a linear regression model to anticipate prices. Plotting a scatter graph to display the 'y true' value vs 'y pred' value will show the prediction results. Output: 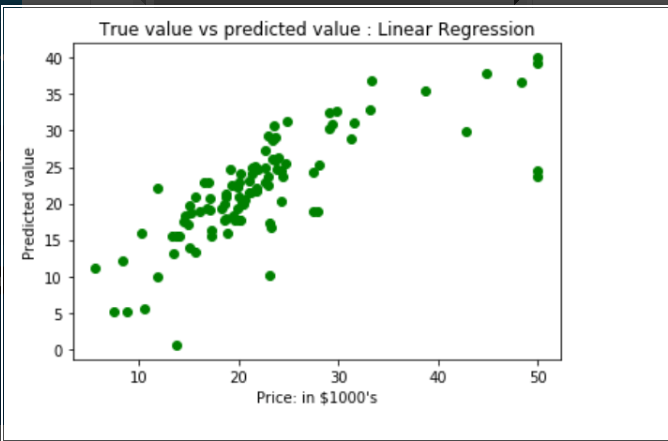
Mean Squared Error & Mean Absolute Error are the results of linear regression. Output: Mean Square Error is : 33.4489799151161496 Mean Absolute Error is : 3.8429092484151966 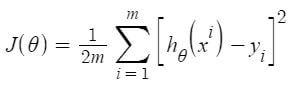
As a result, the accuracy of our model is just 66.55%. The prepared model is therefore not particularly effective in forecasting home prices. Using a wide range of additional machine learning methods and approaches, one can enhance the prediction outcomes.
Next TopicWhat are OpenAI and ChatGPT
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










