Propositional logic in Artificial intelligence
Propositional logic (PL) is the simplest form of logic where all the statements are made by propositions. A proposition is a declarative statement which is either true or false. It is a technique of knowledge representation in logical and mathematical form.
Example:
Following are some basic facts about propositional logic:
- Propositional logic is also called Boolean logic as it works on 0 and 1.
- In propositional logic, we use symbolic variables to represent the logic, and we can use any symbol for a representing a proposition, such A, B, C, P, Q, R, etc.
- Propositions can be either true or false, but it cannot be both.
- Propositional logic consists of an object, relations or function, and logical connectives.
- These connectives are also called logical operators.
- The propositions and connectives are the basic elements of the propositional logic.
- Connectives can be said as a logical operator which connects two sentences.
- A proposition formula which is always true is called tautology, and it is also called a valid sentence.
- A proposition formula which is always false is called Contradiction.
- A proposition formula which has both true and false values is called
- Statements which are questions, commands, or opinions are not propositions such as "Where is Rohini", "How are you", "What is your name", are not propositions.
Syntax of propositional logic:
The syntax of propositional logic defines the allowable sentences for the knowledge representation. There are two types of Propositions:
- Atomic Propositions
- Compound propositions
- Atomic Proposition: Atomic propositions are the simple propositions. It consists of a single proposition symbol. These are the sentences which must be either true or false.
Example:
- Compound proposition: Compound propositions are constructed by combining simpler or atomic propositions, using parenthesis and logical connectives.
Example:
Logical Connectives:
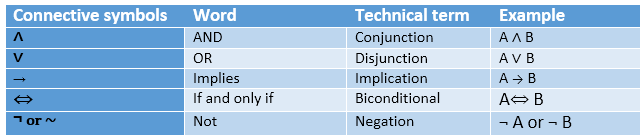
Logical connectives are used to connect two simpler propositions or representing a sentence logically. We can create compound propositions with the help of logical connectives. There are mainly five connectives, which are given as follows:
- Negation: A sentence such as ¬ P is called negation of P. A literal can be either Positive literal or negative literal.
- Conjunction: A sentence which has ∧ connective such as, P ∧ Q is called a conjunction.
Example: Rohan is intelligent and hardworking. It can be written as,
P= Rohan is intelligent,
Q= Rohan is hardworking. → P∧ Q.
- Disjunction: A sentence which has ∨ connective, such as P ∨ Q. is called disjunction, where P and Q are the propositions.
Example: "Ritika is a doctor or Engineer",
Here P= Ritika is Doctor. Q= Ritika is Doctor, so we can write it as P ∨ Q.
- Implication: A sentence such as P → Q, is called an implication. Implications are also known as if-then rules. It can be represented as
If it is raining, then the street is wet.
Let P= It is raining, and Q= Street is wet, so it is represented as P → Q
- Biconditional: A sentence such as P⇔ Q is a Biconditional sentence, example If I am breathing, then I am alive
P= I am breathing, Q= I am alive, it can be represented as P ⇔ Q.
Following is the summarized table for Propositional Logic Connectives:
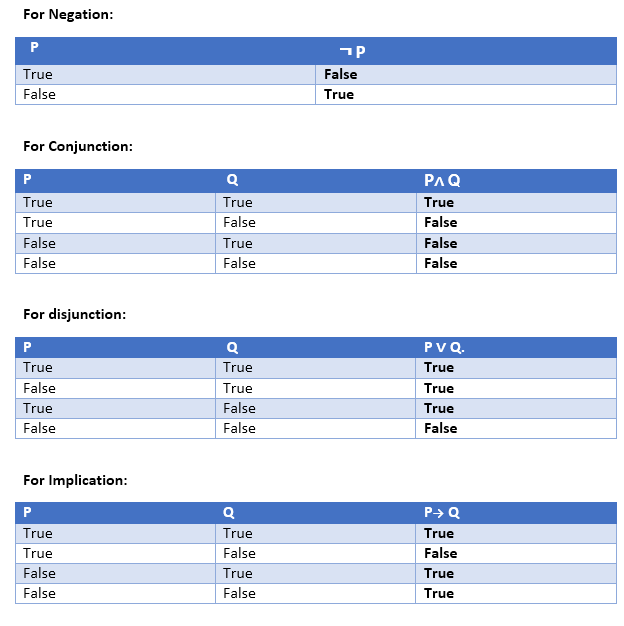
Truth Table:
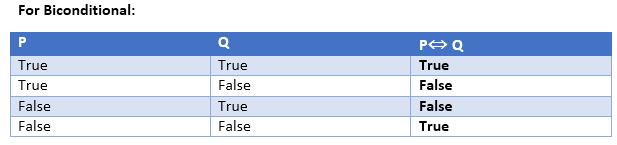
In propositional logic, we need to know the truth values of propositions in all possible scenarios. We can combine all the possible combination with logical connectives, and the representation of these combinations in a tabular format is called Truth table. Following are the truth table for all logical connectives:
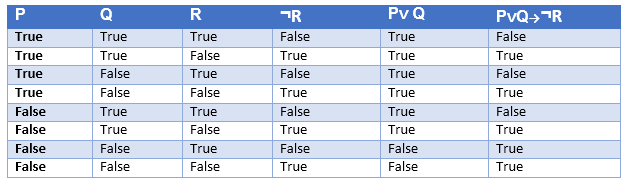
Truth table with three propositions:
We can build a proposition composing three propositions P, Q, and R. This truth table is made-up of 8n Tuples as we have taken three proposition symbols.
Precedence of connectives:
Just like arithmetic operators, there is a precedence order for propositional connectors or logical operators. This order should be followed while evaluating a propositional problem. Following is the list of the precedence order for operators:
| Precedence |
Operators |
| First Precedence |
Parenthesis |
| Second Precedence |
Negation |
| Third Precedence |
Conjunction(AND) |
| Fourth Precedence |
Disjunction(OR) |
| Fifth Precedence |
Implication |
| Six Precedence |
Biconditional |
Note: For better understanding use parenthesis to make sure of the correct interpretations. Such as ¬R∨ Q, It can be interpreted as (¬R) ∨ Q.
Logical equivalence:
Logical equivalence is one of the features of propositional logic. Two propositions are said to be logically equivalent if and only if the columns in the truth table are identical to each other.
Let's take two propositions A and B, so for logical equivalence, we can write it as A⇔B. In below truth table we can see that column for ¬A∨ B and A→B, are identical hence A is Equivalent to B

Properties of Operators:
- Commutativity:
- P∧ Q= Q ∧ P, or
- P ∨ Q = Q ∨ P.
- Associativity:
- (P ∧ Q) ∧ R= P ∧ (Q ∧ R),
- (P ∨ Q) ∨ R= P ∨ (Q ∨ R)
- Identity element:
- P ∧ True = P,
- P ∨ True= True.
- Distributive:
- P∧ (Q ∨ R) = (P ∧ Q) ∨ (P ∧ R).
- P ∨ (Q ∧ R) = (P ∨ Q) ∧ (P ∨ R).
- DE Morgan's Law:
- ¬ (P ∧ Q) = (¬P) ∨ (¬Q)
- ¬ (P ∨ Q) = (¬ P) ∧ (¬Q).
- Double-negation elimination:
Limitations of Propositional logic:
- We cannot represent relations like ALL, some, or none with propositional logic. Example:
- All the girls are intelligent.
- Some apples are sweet.
- Propositional logic has limited expressive power.
- In propositional logic, we cannot describe statements in terms of their properties or logical relationships.
|





 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now









