What is Dilated Convolution?

The term "dilated" refers to the addition of gaps or "holes" in the multilayer kernel, which allows it to have a bigger responsive field without raising the number of parameters.

Dilated convolution, also known as atrous convolution, data is a variant of the standard convolution technique seen in neural networks and signal processing applications.

Advantages

i) Dilated convolutions expand the receptive field without requiring a larger kernel or additional parameters. This is useful for capturing long-term dependencies in datasets.

ii) Sparse Sampling: Dilated convolutions create gaps in the convolutional kernel, which minimizes the amount of computing required compared to a fully linked receptive field. This may result in more efficient processing, particularly regarding memory and computational requirements.

iii) Multi-Scale Information: To capture multi-scale information, utilize dilated convolutions with varying dilation rates. A network can simultaneously record local and global features by stacking layers with different dilation rates.

iv) Spatial Resolution Preservation: Unlike pooling processes, which diminish spatial resolution, dilated convolutions preserve input size.

Disadvantages

i) Limited Local Detail: While dilated convolutions are good at capturing global information, they may be less effective at catching fine-grained local details than standard convolutions, especially when a high level of detail is required.

ii) Not Ideal for All Operations: Dilated convolutions may not be appropriate for all data or operations. Traditional convolutions or other architectural choices may be more effective in certain situations, particularly where the interactions between adjacent pieces are critical.

iii) Potential Overfitting: Depending on the architecture and application, dilated convolutions may increase the danger of overfitting, especially if the dilation rates are not carefully adjusted. This is because a broader receptive field may detect noise in the data.

iv) Learning Curve: Implementing and tweaking dilated convolutional layers may necessitate a greater understanding of the architecture and its hyperparameters, which can be difficult for practitioners unfamiliar with these concepts.

Aspect

i) Dilated Convolution in One and Three Dimensions:

While the above examples employed 2D images, dilated convolution can also be applied to 1D signals (e.g., time series data) and 3D volumes (e.g., video data, medical imaging). The concepts remain the same, with dilation rates influencing the receptive field in many dimensions.

ii) Atrous Spatial Pyramid Pooling (ASPP):

ASPP is a semantic segmentation technique that uses dilated convolutions with varying dilation rates. It enables the network to capture data at many scales, boosting the model's ability to comprehend local and global settings.

iii) Wavenet Architecture:

The WaveNet engineering, a DeepMind-grew profound generative model for discourse blend, utilized expanded convolutions. WaveNet utilizes widened convolutions in a causal way to display long-range conditions in sound sources.

iv) Effective Memory Usage:

Dilated convolutions are more memory efficient than typical convolutional layers with big kernels. This is especially crucial in jobs that involve vast amounts of input data or photos.

v) Dilated Convolutions of Point Clouds:

In computer graphics and computer-aided design (CAD), dilated convolutions have been investigated for analyzing 3D point clouds. They offer a method to efficiently capture spatial correlations in sporadically sampled data.

Application

i) Semantic segmentation:

Enlarged convolutions are regularly utilized in semantic division undertakings, which plan to appoint semantic names to every pixel in a picture. Enlarged convolutions might catch nearby highlights and worldwide settings, which is helpful for fragmenting items and circumstances.

ii) Image Generation:

Dilated convolutions can capture spatial relationships and provide realistic content while preserving fine-grained features in image generation tasks such as creating high-resolution photos or inpainting missing sections.

iii) Object Recognition:

Dilated convolutions are employed in object identification tasks, which aim to recognize and classify items inside an image. Dilated convolutions improve object recognition across scales by allowing the model to examine a broader receptive field without down sampling.

iv) Medical imaging:

In medical image analysis, dilated convolutions are used for tasks such as picture segmentation, which require precise identification of anatomical components. They allow the model to consider a larger context while maintaining the spatial resolution of medical pictures.

v) Natural language processing (NLP):

Dilated convolutions have performed sequence-based NLP tasks such as text categorization and sentiment analysis. Dilated convolutions, considering text a one-dimensional sequence, can capture long-range language dependencies.

Dilation Rate

The dilation rate is a parameter related to dilated convolutions that control the spacing between the components (or "holes") in the convolutional kernel. This parameter determines how much the convolutional filter "skips" over the input data.

In a normal (non-dilated) convolution, each element of the convolutional filter is applied to adjacent elements in the input feature map. However, in dilated convolutions, the dilation rate creates gaps between the elements, extending the receptive field without introducing more parameters.

A single integer or a tuple of integers usually represents the dilation rate. This is how it works.

i) The dilation rate of one corresponds to normal convolution, in which the filter's elements are nearby.

ii) A dilation rate greater than one creates gaps; the higher the dilation rate, the wider the space between the pieces. For example:

- A dilation rate of two indicates that one space exists between the filter's elements.

- A dilation rate of 3 indicates two vacant gaps between the pieces.

And so on.

The dilation rate determines the effective receptive field of the convolution operation. A higher dilation rate absorbs information from a wider spatial range, helping the model to learn long-term dependencies in the data. This is especially important for jobs that require understanding global context, such as image segmentation.

Example with simple Python code

A basic NumPy example for performing 1D dilated convolution. For example, in practice, deep learning tools such as TensorFlow or PyTorch would be more suited to handling convolution operations within neural network structures.

Output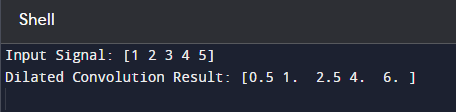

In this example, dilated_convolution_1d is a basic function that applies a 1D dilated convolution on an input signal using a specified kernel and dilation rate. The finished product is then printed for illustration. Deep learning frameworks are recommended for more complicated scenarios due to their efficiency and ease of deployment.

Conclusion

Dilated convolutions, which introduce gaps in the convolutional kernel, provide a convincing solution in deep learning by increasing the receptive field while keeping spatial resolution. Their ability to capture both local details and global context has made them indispensable in various applications, including semantic segmentation, object recognition, and scene understanding. Adapting dilated convolutions across fields, from computer vision to natural language processing, demonstrates flexibility. Notable benefits include efficient memory use, compatibility with cutting-edge architectures, and adaptability for real-time applications. However, the choice of dilation rates remains a critical hyperparameter, highlighting the importance of careful adjustment. To summarize, dilated convolutions are a potent tool that has greatly contributed to advances in neural network topologies and their performance across various tasks.