A* Search Algorithm in Artificial Intelligence

An Introduction to A* Search Algorithm in AI

A* (pronounced "A-star") is a powerful graph traversal and pathfinding algorithm widely used in artificial intelligence and computer science. It is mainly used to find the shortest path between two nodes in a graph, given the estimated cost of getting from the current node to the destination node. The main advantage of the algorithm is its ability to provide an optimal path by exploring the graph in a more informed way compared to traditional search algorithms such as Dijkstra's algorithm.

Algorithm A* combines the advantages of two other search algorithms: Dijkstra's algorithm and Greedy Best-First Search. Like Dijkstra's algorithm, A* ensures that the path found is as short as possible but does so more efficiently by directing its search through a heuristic similar to Greedy Best-First Search. A heuristic function, denoted h(n), estimates the cost of getting from any given node n to the destination node.

The main idea of A* is to evaluate each node based on two parameters:

g(n): the actual cost to get from the initial node to node n. It represents the sum of the costs of node n outgoing edges.
h(n): Heuristic cost (also known as "estimation cost") from node n to destination node n. This problem-specific heuristic function must be acceptable, meaning it never overestimates the actual cost of achieving the goal. The evaluation function of node n is defined as f(n) = g(n) h(n).

Algorithm A* selects the nodes to be explored based on the lowest value of f(n), preferring the nodes with the lowest estimated total cost to reach the goal. The A* algorithm works:

Create an open list of foundbut not explored nodes.
Create a closed list to hold already explored nodes.
Add a startingnode to the open list with an initial value of g
Repeat the following steps until the open list is empty or you reachthe target node:
1. Find the node with the smallest f-value (i.e., the node with the minor g(n) h(n)) in the open list.
2. Move the selected node from the open list to the closed list.
3. Createall valid descendantsof the selected node.
4. For each successor, calculateits g-value as the sum of the current node's g value and the cost of movingfrom the current node to the successor node. Update the g-value of the tracker when a better path is found.
5. If the followeris not in the open list, add it with the calculated g-value and calculate its h-value. If it is already in the open list, update its g value if the new path is better.
6. Repeat the cycle. Algorithm A* terminates when the target node is reached or when the open list empties, indicating no paths from the start node to the target node. The A* search algorithm is widely used in various fields such as robotics, video games, network routing, and design problems because it is efficient and can find optimal paths in graphs or networks.

However, choosing a suitable and acceptable heuristic function is essential so that the algorithm performs correctly and provides an optimal solution.

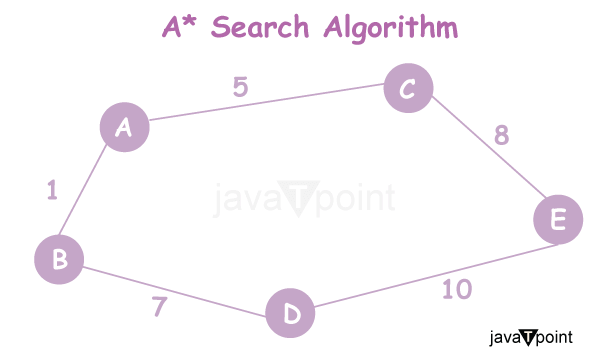
History of the A* Search Algorithm in Artificial Intelligence

It was developed by Peter Hart, Nils Nilsson, and Bertram Raphael at the Stanford Research Institute (now SRI International) as an extension of Dijkstra's algorithm and other search algorithms of the time. A* was first published in 1968 and quickly gained recognition for its importance and effectiveness in the artificial intelligence and computer science communities. Here is a brief overview of the most critical milestones in the history of the search algorithm A*:

Early search algorithms: Before the development of A*, various graph search algorithms existed, including Depth-First Search (DFS) and Breadth-First Search (BFS). Although these algorithms helped find paths, they did not guarantee optimality or consider heuristics to guide the search
Dijkstra's algorithm: In 1959, Dutch computer scientist Edsger W. Dijkstra introduced Dijkstra's algorithm, which found the shortest path in a weighted graph with non-negative edge weights. Dijkstra's algorithm was efficient, but due to its exhaustive nature, it had limitations when used on larger graphs or
Informed Search: Knowledge-based search algorithms (also known as heuristic search) have been developed to incorporate heuristic information, such as estimated costs, to guide the search process efficiently. Greedy Best-First Search was one such algorithm, but it did not guarantee optimality for finding the shortest path.
A* development: In 1968, Peter Hart, Nils Nilsson, and Bertram Raphael introduced the A* algorithm as a combination of Dijkstra's algorithm and Greedy Best-First Search. A* used a heuristic function to estimate the cost from the current node to the destination node by combining it with the actual cost of reaching the current node. This allowed A* to explore the graph more consciously, avoiding unnecessary paths and guaranteeing an optimal solution.
Righteousness and Perfection: The authors of A* showed that the algorithm is perfect (always finds a solution if one exists) and optimal (finds the shortest path) under certain conditions.
Wide-spread adoption and progress: A* quickly gained popularity in the AI and IT communities due to its efficiency and Researchers and developers have extended and applied the A* algorithm to various fields, including robotics, video games, engineering, and network routing. Several variations and optimizations of the A* algorithm have been proposed over the years, such as Incremental A* and Parallel A*. Today, the A* search algorithm is still a fundamental and widely used algorithm in artificial intelligence and graph traversal. It continues to play an essential role in various applications and research fields. Its impact on artificial intelligence and its contribution to pathfinding and optimization problems have made it a cornerstone algorithm in intelligent systems research.

How does the A* search algorithm work in Artificial Intelligence?

The A* (pronounced "letter A") search algorithm is a popular and widely used graph traversal algorithm in artificial intelligence and computer science. It is used to find the shortest path from a start node to a destination node in a weighted graph. A* is an informed search algorithm that uses heuristics to guide the search efficiently. The search algorithm A* works as follows:

The algorithm starts with a priority queue to store the nodes to be explored. It also instantiates two data structures g(n): The cost of the shortest path so far from the starting node to node n and h(n), the estimated cost (heuristic) from node n to the destination node. It is often a reasonable heuristic, meaning it never overestimates the actual cost of achieving a goal. Put the initial node in the priority queue and set its g(n) to 0. If the priority queue is not empty, Remove the node with the lowest f(n) from the priority queue. f(n) = g(n) h(n). If the deleted node is the destination node, the algorithm ends, and the path is found. Otherwise, expand the node and create its neighbors. For each neighbor node, calculate its initial g(n) value, which is the sum of the g value of the current node and the cost of moving from the current node to a neighboring node. If the neighbor node is not in priority order or the original g(n) value is less than its current g value, update its g value and set its parent node to the current node. Calculate the f(n) value from the neighbor node and add it to the priority queue.

If the cycle ends without finding the destination node, the graph has no path from start to finish. The key to the efficiency of A* is its use of a heuristic function h(n) that provides an estimate of the remaining cost of reaching the goal of any node. By combining the actual cost g (n) with the heuristic cost h (n), the algorithm effectively explores promising paths, prioritizing nodes likely to lead to the shortest path. It is important to note that the efficiency of the A* algorithm is highly dependent on the choice of the heuristic function. Acceptable heuristics ensure that the algorithm always finds the shortest path, but more informed and accurate heuristics can lead to faster convergence and reduced search space.

Advantages of A* Search Algorithm in Artificial Intelligence

The A* search algorithm offers several advantages in artificial intelligence and problem-solving scenarios:

Optimal solution: A* ensures finding the optimal (shortest) path from the start node to the destination node in the weighted graph given an acceptable heuristic function. This optimality is a decisive advantage in many applications where finding the shortest path is essential.
Completeness: If a solution exists, A* will find it, provided the graph does not have an infinite cost This completeness property ensures that A* can take advantage of a solution if it exists.
Efficiency: A* is efficient ifan efficient and acceptable heuristic function is used. Heuristics guide the search to a goal by focusing on promising paths and avoiding unnecessary exploration, making A* more efficient than non-aware search algorithms such as breadth-first search or depth-first search.
Versatility: A* is widely applicable to variousproblem areas, including wayfinding, route planning, robotics, game development, and more. A* can be used to find optimal solutions efficiently as long as a meaningful heuristic can be defined.
Optimized search: A* maintains a priority order to select the nodes with the minor f(n) value (g(n) and h(n)) for expansion. This allows it to explore promising paths first, which reduces the search space and leads to faster convergence.
Memory efficiency: Unlike some other search algorithms, such as breadth-first search, A* stores only a limited number of nodes in the priority queue, which makes it memory efficient, especially for large graphs.
Tunable Heuristics: A*'s performancecan be fine-tuned by selecting different heuristic functions. More educated heuristics can lead to faster convergence and less expanded nodes.
Extensively researched: A* is a well-established algorithm with decades of research and practical applications. Many optimizations and variations have been developed, making it a reliable and well-understood troubleshooting tool.
Web search: A* can be used for web-based path search, where the algorithm constantly updates the path according to changes in the environment or the appearance of new It enables real-time decision-making in dynamic scenarios.

Disadvantages of A* Search Algorithm in Artificial Intelligence

Although the A* (letter A) search algorithm is a widely used and powerful technique for solving AI pathfinding and graph traversal problems, it has disadvantages and limitations. Here are some of the main disadvantages of the search algorithm:

Heuristic accuracy: The performance of the A* algorithm depends heavily on the accuracy of the heuristic function used to estimate the cost from the current node to the If the heuristic is unacceptable (never overestimates the actual cost) or inconsistent (satisfies the triangle inequality), A* may not find an optimal path or may explore more nodes than necessary, affecting its efficiency and accuracy.
Memory usage: A* requires that all visited nodes be kept in memory to keep track of explored paths. Memory usage can sometimes become a significant issue, especially when dealing with an ample search space or limited memory resources.
Time complexity: AlthoughA* is generally efficient, its time complexity can be a concern for vast search spaces or graphs. In the worst case, A* can take exponentially longer to find the optimal path if the heuristic is inappropriate for the problem.
Bottleneck at the destination: In specific scenarios, the A* algorithm needs to explore nodes far from the destination before finally reaching the destination region. This the problem occurs when the heuristic needs to direct the search to the goal early effectively.
Cost Binding: A* faces difficulties when multiple nodes have the same f-value (the sum of the actual cost and the heuristic cost). The strategy used can affect the optimality and efficiency of the discovered path. If not handled correctly, it can lead to unnecessary nodes being explored and slow down the algorithm.
Complexity in dynamic environments: In dynamic environments where the cost of edges or nodes may change during the search, A* may not be suitable because it does not adapt well to such changes. Reformulation from scratch can be computationally expensive, and D* (Dynamic A*) algorithms were designed to solve this
Perfection in infinite space : A* may not find a solution in infinite state space. In such cases, it can run indefinitely, exploring an ever-increasing number of nodes without finding a solution. Despite these shortcomings, A* is still a robust and widely used algorithm because it can effectively find optimal paths in many practical situations if the heuristic function is well-designed and the search space is manageable. Various variations and variants of A* have been proposed to alleviate some of its limitations.

Applications of the A* Search Algorithm in Artificial Intelligence

The search algorithm A* (letter A) is a widely used and robust pathfinding algorithm in artificial intelligence and computer science. Its efficiency and optimality make it suitable for various applications. Here are some typical applications of the A* search algorithm in artificial intelligence:

Pathfinding in Games: A* is oftenused in video games for character movement, enemy AI navigation, and finding the shortest path from one location to another on the game map. Its ability to find the optimal path based on cost and heuristics makes it ideal for real-time applications such as games.
Robotics and Autonomous Vehicles: A* is used in robotics and autonomous vehicle navigation to plan anoptimal route for robots to reach a destination, avoiding obstacles and considering terrain costs. This is crucial for efficient and safe movement in natural environments.
Maze solving: A* can efficiently find the shortest path through a maze, making it valuable in many maze-solving applications, such as solving puzzles or navigating complex structures.
Route planningand navigation: In GPS systems and mapping applications, A* can be used to find the optimal route between two points on a map, considering factors such as distance, traffic conditions, and road network topology.
Puzzle-solving: A* can solve various diagram puzzles, such as sliding puzzles, Sudoku, and the 8-puzzle problem. Resource Allocation: In scenarios where resources must be optimally allocated, A* can help find the most efficient allocation path, minimizing cost and maximizing efficiency.
Network Routing: A* can be usedin computer networks to find the most efficient route for data packets from a source to a destination node.
Natural Language Processing (NLP): In some NLP tasks, A* can generate coherent and contextualresponses by searching for possible word sequences based on their likelihood and relevance.
Path planningin robotics: A* can be used to plan the path of a robot from one point to another, considering various constraints, such as avoiding obstacles or minimizing energy consumption.
Game AI: A* is also used to makeintelligent decisions for non-player characters (NPCs), such as determining the best way to reach an objective or coordinate movements in a team-based game.

These are just a few examples of how the A* search algorithm finds applications in various areas of artificial intelligence. Its flexibility, efficiency, and optimization make it a valuable tool for many problems.

C program for A* Search Algorithm in Artificial Intelligence

#include <stdio.h>
#include <stdlib.h>

#define ROWS 5
#define COLS 5

// Define a structure for a grid cell
typedef struct {
    int row, col;
} Cell;

// Define a structure for a node in the A* algorithm
typedef struct {
    Cell position;
    int g, h, f;
    struct Node* parent;
} Node;

// Function to calculate the Manhattan distance between two cells
int heuristic(Cell current, Cell goal) {
    return abs(current.row - goal.row) + abs(current.col - goal.col);
}

// Function to check if a cell is valid (within the grid and not an obstacle)
int isValid(int row, int col, int grid[ROWS][COLS]) {
    return (row >= 0) && (row < ROWS) && (col >= 0) && (col < COLS) && (grid[row][col] == 0);
}

// Function to check if a cell is the goal cell
int isGoal(Cell cell, Cell goal) {
    return (cell.row == goal.row) && (cell.col == goal.col);
}

// Function to perform the A* search algorithm
void AStarSearch(int grid[ROWS][COLS], Cell start, Cell goal) {
    // TODO: Implement the A* search algorithm here
}

int main() {
    int grid[ROWS][COLS] = {
        {0, 1, 0, 0, 0},
        {0, 1, 0, 1, 0},
        {0, 0, 0, 1, 0},
        {0, 1, 0, 0, 0},
        {0, 0, 0, 0, 0}
    };
    
    Cell start = {0, 0};
    Cell goal = {ROWS - 1, COLS - 1};
    
    AStarSearch (grid, start, goal);

    return 0;
}

Explanation:

Data Structures: A cell structure represents a grid cell with a row and a column. The node structure stores information about a cell during an A* lookup, including its location, cost (g, h, f), and a reference to its parent.
Heuristic function (heuristic): This function calculates the Manhattan distance (also known as a "cab ride") between two cells. It is used as a heuristic to estimate the cost from the current cell to the target cell. The Manhattan distance is the sum of the absolute differences between rows and columns.
Validation function (isValid): This function checks if the given cell is valid, i.e., whether it is within the grid boundaries and is not an obstacle (indicated by a grid value of 1).
Goal check function (isGoal): This function checks if the given cell is a target cell, i.e., does it match the coordinates of the target cell.
Search function* (AStarSearch): This is the main function where the A* search algorithm should be applied. It takes a grid, a source cell, and a target cell as inputs. This activity aims to find the shortest path from the beginning to the end, avoiding the obstacles on the grid. The main function initializes a grid representing the environment, a start, and a target cell. It then calls the AStarSearch function with those inputs.

Sample Output

(0, 0) (1, 0) (2, 0) (3, 0) (4, 0) (4, 1) (4, 2) (4, 3) (4, 4)

C++ program for A* Search Algorithm in Artificial Intelligence

#include <iostream>
#include <vector>
#include <queue>

using namespace std;

struct Node {
    int x, y; // Coordinates of the node
    int g; // Cost from the start node to this node
    int h; // Heuristic value (estimated cost from this node to the goal node)
    Node* parent; // Parent node in the path

    Node (int x, int y): x(x), y(y), g(0), h(0), parent(nullptr) {}

    // Calculate the total cost (f = g + h)
    int f () const {
        return g + h;
    }
};

// Heuristic function (Euclidean distance)
int calculateHeuristic (int x, int y, int goals, int goal) {
    return static cast<int> (sqrt (pow (goals - x, 2) + pow (goal - y, 2)));
}

// A* search algorithm
vector<pair<int, int>> AStarSearch (int startX, int startY, int goals, int goal, vector<vector<int>>& grid) {
    vector<pair<int, int>> path;
    int rows = grid. size ();
    int cols = grid [0].size ();

    // Create the open and closed lists
    Priority queue <Node*, vector<Node*>, function<bool (Node*, Node*)>> open List([](Node* lhs, Node* rhs) {
        return lhs->f() > rhs->f();
    });
    vector<vector<bool>> closed List (rows, vector<bool> (cols, false));


    // Push the start node to the open list
    openList.push(start Node);

    // Main A* search loop
    while (! Open-list. Empty ()) {
        // Get the node with the lowest f value from the open list
        Node* current = open-list. Top ();
        openest. pop ();

        // Check if the current node is the goal node
        if (current->x == goals && current->y == goal) {
            // Reconstruct the path
            while (current! = nullptr) {
                path. push_back(make_pair(current->x, current->y));
                current = current->parent;
            }
            Reverse (path. Begin(), path.end ());
            break;
        }

        // Mark the current node as visited (in the closed list)
        Closed-list [current->x] [current->y] = true;

        // Generate successors (adjacent nodes)
        int dx [] = {1, 0, -1, 0};
        int dy [] = {0, 1, 0, -1};

        for (int i = 0; i < 4; i++) {
            int new X = current->x + dx [i];
            int new Y = current->y + dy [i];


                        }
                        break;
                    }
                

                    successor->parent = current;
                    open List.push(successor);
                }
    // Cleanup memory
    for (Node* node: open List) {
        delete node;
    }

    return path;
}

int main () {
    int rows, cols;
    cout << "Enter the number of rows: ";
    cin >> rows;
    cout << "Enter the number of columns: ";
    cin >> cols;

    vector<vector<int>> grid (rows, vector<int>(cols));

    cout << "Enter the grid (0 for empty, 1 for obstacle):" << endl;
    for (int i = 0; i < rows; i++) {
        for (int j = 0; j < cols; j++) {
            cin >> grid[i][j];
        }
    }

    int startX, startY, goalX, goalY;
    cout << "Enter the start coordinates (x y): ";
    cin >> startX >> start;
    cout << "Enter the goal coordinates (x y): ";
    cin >> goals >> goals;

    vector<pair<int, int>> path = AStarSearch (startX, startY, goal, goal, grid);

    if (! path. Empty ()) {
        cout << "Shortest path from (" << startX << "," << start << ") to (" << goal << "," << goal << "):" << endl;
        for (const auto& point: path) {
            cout << "(" << point. first << "," << point. second << ") ";
        }
        cout << endl;
    } else {
        cout << "No path found!" << endl;
    }

    return 0;
}

Explanation:

Struct Node: This defines a nodestructure that represents a grid cell. It contains the x and y coordinates of the node, the cost g from the starting node to that node, the heuristic value h (estimated cost from that node to the destination node), and a pointer to the
starting node of the path.
Calculate heuristic: This function calculates a heuristic using the Euclidean distance between a node and the target AStarSearch: This function runs the A* search algorithm. It takes the start and destination coordinates, a grid, and returns a vector of pairs representing the coordinates of the shortest path from start to finish.
Primary: The program's main function takes input grids, origin, and target coordinates from the user. It then calls AStarSearch to find the shortest path and prints the result. Struct Node: This defines a node structure that represents a grid cell. It contains the x and y coordinates of the node, the cost g from the starting node to that node, the heuristic value h (estimated cost from that node to the destination node), and a pointer to the starting node of the path.
Calculate heuristic: This function calculates heuristics using the Euclidean distance between a node and the target AStarSearch: This function runs the A* search algorithm. It takes the start and destination coordinates, a grid, and returns a vector of pairs representing the coordinates of the shortest path from start to finish.

Sample Output

Enter the number of rows: 5
Enter the number of columns: 5
Enter the grid (0 for empty, 1 for obstacle):
0 0 0 0 0
0 1 1 1 0
0 0 1 0 0
0 0 0 1 0
0 0 0 0 0
Enter the start coordinates (x y): 0 0
Enter the goal coordinates (x y): 4 4

Java program for A* Search Algorithm in Artificial Intelligence

import java. util.*;

class Node {
    int x, y; // Coordinates of the node
    int g; // Cost from the start node to the current node
    int h; // Heuristic value (estimated cost from the current node to goal node)
    int f; // Total cost f = g + h
    Node parent; // Parent node in the path

    public Node (int x, int y) {
        this. g = x;
        this. f = y;
        
        this. Parent = null;
    }
}

public class AStarSearch {

    // Heuristic function (Manhattan distance)
    private static int heuristic (Node current, Node goal) {
        return Math. Abs (current.x - goal.x) + Math. Abs(current.y - goal.y);
    }

    // A* search algorithm
    public static List<Node> aStarSearch(int [][] grid, Node start, Node goal) {
        int rows = grid. Length;
        int cols = grid   [0].length;


        // Add the start node to the open set
        opened.add(start);

        while (! openSet.isEmpty()) {
            // Get the node with the lowest f value from the open set
            Node current = openSet.poll();

            // If the current node is the goal node, reconstruct the path and return it
            if (current == goal) {
                List<Node> path = new ArrayList<>();
                while (current != null) {
                    path.add(0, current);
                    current = current.parent;
                }
                return path;
            }

            // Move the current node from the open set to the closed set
            closedSet.add(current);

            // Generate neighbors of the current node
            int[] dx = {-1, 0, 1, 0};
            int[] dy = {0, -1, 0, 1};

            for (int i = 0; i < 4; i++) {
                int nx = current.x + dx[i];
                int ny = current.y + dy[i];

                // Check if the neighbor is within the grid boundaries
                if (nx >= 0 && nx < rows && ny >= 0 && ny < cols && grid[nx][ny] == 0) {
                    Node neighbor = new Node(nx, ny);
                    int tentativeG = current.g + 1; // Assuming each step cost is 1

                    if (closedSet.contains(neighbor) && tentativeG >= neighbor.g) {
                        // Skip this neighbor as it is already in the closed set with a lower or equal g value
                        continue;
                    }

                    if (!openSet.contains(neighbor) || tentativeG < neighbor.g) {
                        // Update the neighbor's values
                        neighbor.g = tentativeG;
                        neighbor.h = heuristic(neighbor, goal);
                        neighbor.f = neighbor.g + neighbor.h;
                        neighbor.parent = current;

                        if (!openSet.contains(neighbor)) {
                            // Add the neighbor to the open set if not already present
                            openSet.add(neighbor);
                        }
                    }
                }
            }
        }

        // If the open set is empty and the goal is not reached, there is no path
        return null;
    }

    public static void main(String[] args) {
        int[][] grid = {
            {0, 0, 0, 0, 0},
            {0, 1, 0, 1, 0},
            {0, 0, 0, 0, 0},
            {0, 1, 0, 1, 0},
            {0, 0, 0, 0, 0}
        };

        Node start = new Node(0, 0);
        Node goal = new Node(4, 4);

        List<Node> path = aStarSearch(grid, start, goal);

        if (path != null) {
            System.out.println("Path found:");
            for (Node node : path) {
                System.out.println("(" + node.x + ", " + node.y + ")");
            }
        } else {
            System.out.println("No path found.");
        }
    }
}

Explanation:

Node Class: We start by defining a nodeclass representing each grid cell. Each node contains coordinates (x, y), an initial node cost (g), a heuristic value (h), a total cost (f = g h), and a reference to the parent node of the path.
Heuristicfunction: The heuristic function calculates the Manhattan distance between a node and a destination The Manhattan distance is a heuristic used to estimate the cost from the current node to the destination node.
Search algorithm* function: A Star Search is the primary implementation of the search algorithm A*. It takes a 2D grid, a start node, and a destination node as inputs and returns a list of nodes representing the path from the start to the destination node.
Priority Queue and Closed Set: The algorithm uses a priority queue (open Set) to track thenodes to be explored. The queue is ordered by total cost f, so the node with the lowest f value is examined The algorithm also uses a set (closed set) to track the explored nodes.
The main loop of the algorithm: The main loop of the A* algorithm repeats until there are no more nodes to explore in the open Set. In each iteration, the node f with the lowest total cost is removed from the opener, and its neighbors are created.
Creating neighbors: The algorithm creates four neighbors (up, down, left, right) for each node and verifies that each neighbor is valid (within the network boundaries and not as an obstacle). If the neighbor is valid, it calculates the initial value g from the source node to that neighbor and the heuristic value h from that neighbor to the destination The total cost is then calculated as the sum of f, g, and h.
Node evaluation: The algorithm checks whether the neighbor is already in the closed set and, if so, whether the initial cost g is greater than or equal to the existing cost of the neighbor If true, the neighbor is omitted. Otherwise, the neighbor values are updated and added to the open Set if it is not already there.
Pathreconstruction: When the destination node is reached, the algorithm reconstructs the path from the start node to the destination node following the main links from the destination node back to the start node. The path is returned as a list of nodes

Sample Output

Path found:
(0, 0)
(0, 1)
(1, 1)
(2, 1)
(2, 2)
(3, 2)
(4, 2)
(4, 3)
(4, 4)

A* Search Algorithm Complexity in Artificial Intelligence

The A* (pronounced "A-star") search algorithm is a popular and widely used graph traversal and path search algorithm in artificial intelligence. Finding the shortest path between two nodes in a graph or grid-based environment is usually common. The algorithm combines Dijkstra's and greedy best-first search elements to explore the search space while ensuring optimality efficiently. Several factors determine the complexity of the A* search algorithm. Graph size (nodes and edges): A graph's number of nodes and edges greatly affects the algorithm's complexity. More nodes and edges mean more possible options to explore, which can increase the execution time of the algorithm.

Heuristic function: A* uses a heuristic function (often denoted h(n)) to estimate the cost from the current node to the destination node. The precision of this heuristic greatly affects the efficiency of the A* search. A good heuristic can help guide the search to a goal more quickly, while a bad heuristic can lead to unnecessary searching.

Data Structures: A* maintains two maindata structures: an open list (priority queue) and a closed list (or visited pool). The efficiency of these data structures, along with the chosen implementation (e.g., priority queue binary heaps), affects the algorithm's performance.
Branch factor: The average number of followers for each node affects the number of nodes expanded during the search. A higher branching factor can lead to more exploration, which increases
Optimality and completeness: A* guarantees both optimality (finding the shortest path) and completeness (finding a solution that exists). However, this guarantee comes with a trade-off in terms of computational complexity, as the algorithm must explore different paths for optimal performance. Regarding time complexity, the chosen heuristic function affects A* in the worst case. With an accepted heuristic (which never overestimates the true cost of reaching the goal), A* expands the fewest nodes among the optimization algorithms. The worst-case time complexity of A * is exponential in the worst-case O(b ^ d), where "b" is the effective branching factor (average number of followers per node) and "d" is the optimal

In practice, however, A* often performs significantly better due to the influence of a heuristic function that helps guide the algorithm to promising paths. In the case of a well-designed heuristic, the effective branching factor is much smaller, which leads to a faster approach to the optimal solution.

Next TopicHill Climbing Algorithm in AI

← prev next →