Iterative Deepening A* Algorithm (IDA*)Continually Deepening The depth-first search and A* search's greatest qualities are combined in the heuristic search algorithm known as the A* algorithm (IDA*). The shortest route between the start state and the objective state in a network or tree is found using an optimum search method. The IDA* algorithm uses less memory than the A* algorithm because it simply keeps track of the present node and its associated cost, rather than the full search space that has been examined. This article will examine the IDA* algorithm's operation, as well as its benefits and drawbacks, and practical applications. Introduction to Heuristic Search AlgorithmsIn order to identify the best solution to a problem, heuristic search algorithms explore the search area in a methodical manner. They are employed in a number of fields, including robotics, video games, and natural language processing. A heuristic search algorithm uses a heuristic function to evaluate the distance between the current state and the goal state in order to identify the shortest route from the start state to the goal state. There are various heuristic search algorithms, including A* search, Uniform Cost Search (UCS), Depth-First Search (DFS), and Breadth-First Search (BFS). A* Search AlgorithmA* search algorithm is a well-known heuristic search method that calculates the distance between the current state and the objective state using a heuristic function. The A* search method adds the actual cost from the start node to the current node and the predicted cost from the current node to the target node to determine the cost of each node. A heuristic function that estimates the distance between the current node and the desired node is used to determine the estimated cost. The algorithm then chooses the node with the lowest cost, grows it, and keeps doing this until it reaches the destination node. As long as the heuristic function is acceptable and consistent, the A* search algorithm assures finding the shortest path to the destination node. This makes it an ideal search method. A heuristic function is considered acceptable if it never overestimates the destination node's distance. According to the triangle inequality, a consistent heuristic function is one in which the estimated cost from the current node to the target node is less than or equal to the actual cost plus the estimated cost from the next node to the goal node. Iterative Deepening A* AlgorithmIn terms of memory utilisation, the IDA* algorithm outperforms the A* search algorithm. The whole examined search space is kept in memory by the A* search method, which can be memory-intensive for large search spaces. Contrarily, the IDA* method just saves the current node and its associated cost, not the whole searched area. In order to explore the search space, the IDA* method employs depth-first search. Starting with a threshold value equal to the heuristic function's anticipated cost from the start node to the destination node. After that, it expands nodes with an overall price less than or equivalent to the threshold value via a depth-first search starting at the start node. The method ends with the best answer if the goal node is located. The algorithm raises the threshold value to the minimal cost of the nodes that were not extended if the threshold value is surpassed. Once the objective node has been located, the algorithm then repeats the procedure. The IDA* method is full and optimum in the sense that it always finds the best solution if one exists and stops searching if none is discovered. The technique uses less memory since it just saves the current node and its associated cost, not the full search space that has been investigated. Routing, scheduling, and gaming are a few examples of real-world applications where the IDA* method is often employed. Steps for Iterative Deepening A* Algorithm (IDA*)The IDA* algorithm includes the following steps:
The algorithm begins with an initial cost limit, which is usually set to the heuristic cost estimate of the optimal path to the goal node.
The algorithm performs a DFS search from the starting node until it reaches a node with a cost that exceeds the current cost limit.
If the goal node is found during the DFS search, the algorithm returns the optimal path to the goal.
If the goal node is not found during the DFS search, the algorithm updates the cost limit to the minimum cost of any node that was expanded during the search.
The algorithm repeats the process, increasing the cost limit each time until the goal node is found. Example ImplementationLet's look at a graph example to see how the Iterative Deepening A* (IDA*) technique functions. Assume we have the graph below, where the figures in parenthesis represent the expense of travelling between the nodes: 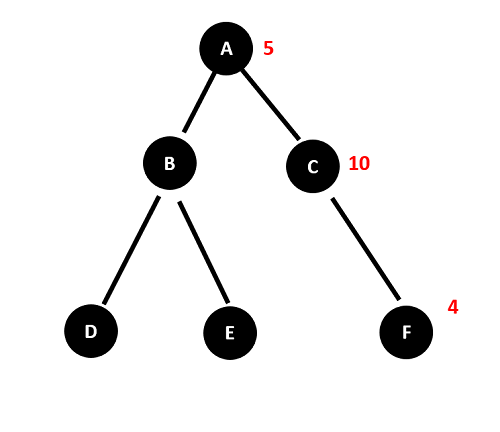
We want to find the optimal path from node A to node F using the IDA* algorithm. The first step is to set an initial cost limit. Let's use the heuristic estimate of the optimal path, which is 7 (the sum of the costs from A to C to F).
We're done since the ideal route was discovered within the initial pricing range. We would have adjusted the cost limit to the lowest cost of any node that was enlarged throughout the search and then repeated the procedure until the goal node was located if the best path could not be discovered within the cost limit. A strong and adaptable search algorithm, the IDA* method may be used to identify the best course of action in a variety of situations. It effectively searches huge state spaces and, if there is an optimal solution, finds it by combining the benefits of DFS and A* search. Advantages
Disadvantages
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









