Viterbi Algorithm in NLPWhat is Viterbi Algorithm?The Viterbi algorithm is a dynamic programming algorithm for determining the best probability estimate of the most likely sequence of hidden states resulting in the order of observed events, particularly in the context of Markov information sources and hidden Markov models (HMM). The Viterbi algorithm aims to produce an assumption based on a trained model and some observed data. It first asks about the most likely choice given the data and the trained model. We can calculate and analyze it by this formula: 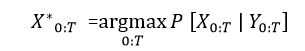
This formula will find the states that can maximize the conditional probability of the states of the data. We can use the given formula to find the best set of states using recursion: 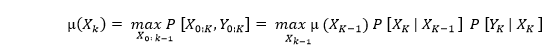
This is the mu function, and it works with the first formula. The technique has widespread use in decoding the convolutional codes used in digital cellular CDMA and GSM, dial-up modems, satellite, and deep-space communications. It is now widely utilized in speech recognition, keyword spotting, computational linguistics, and bioinformatics applications. In speech-to-text (speech recognition), for example, the sound wave is seen as the observed sequence of events, while a string of text is regarded as the "hidden cause" of the acoustic signal. Given an acoustic stimulus, the Viterbi algorithm finds the most likely text string. Hidden Markov Model ( HMM )The Hidden Markov Model is a model used in statistics to define the relationship of probability between a sequence of hidden states and observation. It can be used with any process's hidden observations, thus getting its name, Hidden Markov Model. It predicts future observations based on the hidden process responsible for generating data. It has two types of variables:
Hidden Markov Model and Viterbi AlgorithmThe Viterbi Algorithm is the approach used in the Hidden Markov Model. It calculates the most probable hidden states. Also, it predicts future possibilities, studies the sequential data, and analyzes the patterns. How does the Viterbi Algorithm Work?The Hidden Markov Model first defines the state and observation space. Then, the probability distribution of the initial state is defined. The model is then trained. After the training, the Viterbi Algorithm is used to decode the most likely hidden state sequences. The technique delivers the log probability of the most likely hidden state sequence and the hidden state sequence itself. Then, this algorithm checks the accuracy and performance of the model. Let's understand the Viterbi Algorithm with the help of a program in Python. Program 1: Program to illustrate the Viterbi Algorithm and Hidden Markov Model in Python.Problem Statement: Here, we are provided with the weather data. We have to predict the weather conditions for the future with the help of the current weather conditions. 1. Importing Libraries Code: We have imported numpy, matplotlib, seaborn for visualization and hmmlearn for the predictions. 2. Initialising the parameters Code: Output: Number of hidden states : 3 Number of observations : 3 Explanation: We have initialized different state space, which includes Sunny, Rainy, and Winter. Then, we have defined the observation space, which has different observations like Dry, Wet, and Humid. Code: Output: The State probability: [0.5 0.4 0.1] The Transition probability: [[0.2 0.3 0.5] [0.3 0.4 0.3] [0.5 0.3 0.2]] The Emission probability: [[0.2 0.1 0.7] [0.2 0.5 0.3] [0.4 0.2 0.4] Explanation: We have defined the initial state probability, transition probability, and emission probability in arrays. The state probability defines the probability of the beginning in every hidden state. The transition probability defines the probability of transitioning from one state to another. The emission probability defines the probability of checking the observations in each hidden state. 3. Building the Model Code: Explanation: We have made the HMM model using the categoricalHMM. The model's parameters are set with the state probability, transition, and emission probability. 4. Observation Sequence Code: Output:
array([[1],
[1],
[0],
[1],
[1]])
Explanation: The observed data is defined in a sequence of a numpy array representing different observations. 5. Sequence of hidden states Code: Output: The Most likely hidden states are: [1 1 2 1 1] Explanation: We have predicted the most likely sequence of the hidden states using the HMM model. 6. Decoding the observation sequence Code: Output: Log Probability : -8.845697258388274 Most likely hidden states: [1 1 2 1 1] Explanation: Using the Viterbi Algorithm, we have decoded the observation sequence and calculated the log probability. 7. Data Visualisation Code: Output: 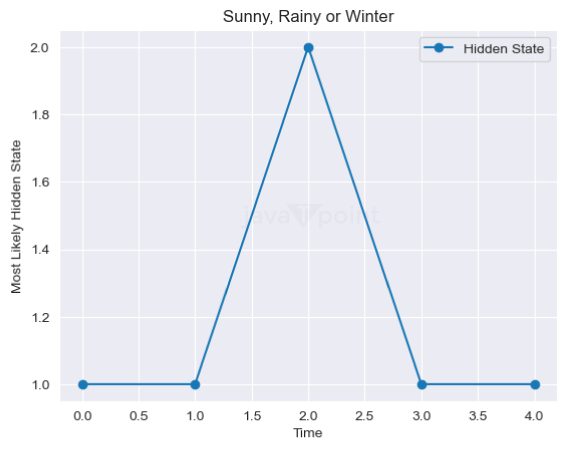
Explanation: We have plotted a graph displaying the results between the period and the hidden states. |
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









