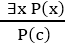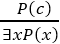Inference in First-Order LogicInference in First-Order Logic is used to deduce new facts or sentences from existing sentences. Before understanding the FOL inference rule, let's understand some basic terminologies used in FOL. Substitution: Substitution is a fundamental operation performed on terms and formulas. It occurs in all inference systems in first-order logic. The substitution is complex in the presence of quantifiers in FOL. If we write F[a/x], so it refers to substitute a constant "a" in place of variable "x". Note: First-order logic is capable of expressing facts about some or all objects in the universe.Equality: First-Order logic does not only use predicate and terms for making atomic sentences but also uses another way, which is equality in FOL. For this, we can use equality symbols which specify that the two terms refer to the same object. Example: Brother (John) = Smith. As in the above example, the object referred by the Brother (John) is similar to the object referred by Smith. The equality symbol can also be used with negation to represent that two terms are not the same objects. Example: ¬(x=y) which is equivalent to x ≠y. FOL inference rules for quantifier:As propositional logic we also have inference rules in first-order logic, so following are some basic inference rules in FOL:
1. Universal Generalization:
Example: Let's represent, P(c): "A byte contains 8 bits", so for ∀ x P(x) "All bytes contain 8 bits.", it will also be true. 2. Universal Instantiation:
Example:1. IF "Every person like ice-cream"=> ∀x P(x) so we can infer that Example: 2. Let's take a famous example, "All kings who are greedy are Evil." So let our knowledge base contains this detail as in the form of FOL: ∀x king(x) ∧ greedy (x) → Evil (x), So from this information, we can infer any of the following statements using Universal Instantiation:
3. Existential Instantiation:
Example: From the given sentence: ∃x Crown(x) ∧ OnHead(x, John), So we can infer: Crown(K) ∧ OnHead( K, John), as long as K does not appear in the knowledge base.
4. Existential introduction
Generalized Modus Ponens Rule:For the inference process in FOL, we have a single inference rule which is called Generalized Modus Ponens. It is lifted version of Modus ponens. Generalized Modus Ponens can be summarized as, " P implies Q and P is asserted to be true, therefore Q must be True." According to Modus Ponens, for atomic sentences pi, pi', q. Where there is a substitution θ such that SUBST (θ, pi',) = SUBST(θ, pi), it can be represented as: 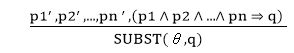
Example: We will use this rule for Kings are evil, so we will find some x such that x is king, and x is greedy so we can infer that x is evil.
Next TopicUnification in First-order logic
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share




 .
.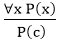 .
.