Uninformed Search AlgorithmsUninformed search is a class of general-purpose search algorithms which operates in brute force-way. Uninformed search algorithms do not have additional information about state or search space other than how to traverse the tree, so it is also called blind search. Following are the various types of uninformed search algorithms:
1. Breadth-first Search:
Advantages:
Disadvantages:
Example:In the below tree structure, we have shown the traversing of the tree using BFS algorithm from the root node S to goal node K. BFS search algorithm traverse in layers, so it will follow the path which is shown by the dotted arrow, and the traversed path will be: 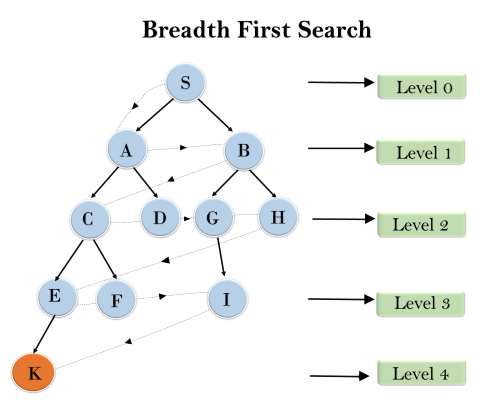
Time Complexity: Time Complexity of BFS algorithm can be obtained by the number of nodes traversed in BFS until the shallowest Node. Where the d= depth of shallowest solution and b is a node at every state. T (b) = 1+b2+b3+.......+ bd= O (bd) Space Complexity: Space complexity of BFS algorithm is given by the Memory size of frontier which is O(bd). Completeness: BFS is complete, which means if the shallowest goal node is at some finite depth, then BFS will find a solution. Optimality: BFS is optimal if path cost is a non-decreasing function of the depth of the node. 2. Depth-first Search
Note: Backtracking is an algorithm technique for finding all possible solutions using recursion.Advantage:
Disadvantage:
Example:In the below search tree, we have shown the flow of depth-first search, and it will follow the order as: Root node--->Left node ----> right node. It will start searching from root node S, and traverse A, then B, then D and E, after traversing E, it will backtrack the tree as E has no other successor and still goal node is not found. After backtracking it will traverse node C and then G, and here it will terminate as it found goal node. 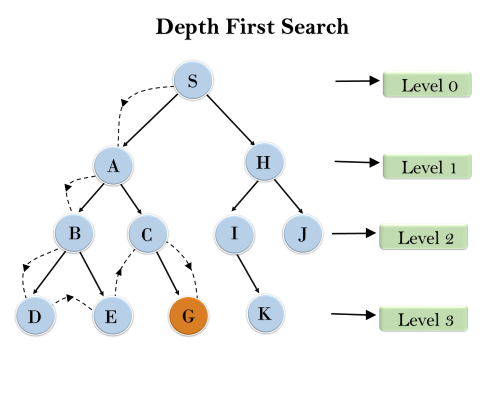
Completeness: DFS search algorithm is complete within finite state space as it will expand every node within a limited search tree. Time Complexity: Time complexity of DFS will be equivalent to the node traversed by the algorithm. It is given by: T(n)= 1+ n2+ n3 +.........+ nm=O(nm) Where, m= maximum depth of any node and this can be much larger than d (Shallowest solution depth) Space Complexity: DFS algorithm needs to store only single path from the root node, hence space complexity of DFS is equivalent to the size of the fringe set, which is O(bm). Optimal: DFS search algorithm is non-optimal, as it may generate a large number of steps or high cost to reach to the goal node. 3. Depth-Limited Search Algorithm:A depth-limited search algorithm is similar to depth-first search with a predetermined limit. Depth-limited search can solve the drawback of the infinite path in the Depth-first search. In this algorithm, the node at the depth limit will treat as it has no successor nodes further. Depth-limited search can be terminated with two Conditions of failure:
Advantages: Depth-limited search is Memory efficient. Disadvantages:
Example: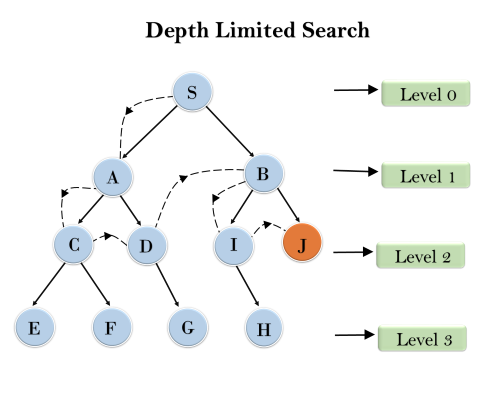
Completeness: DLS search algorithm is complete if the solution is above the depth-limit. Time Complexity: Time complexity of DLS algorithm is O(bℓ). Space Complexity: Space complexity of DLS algorithm is O(b�ℓ). Optimal: Depth-limited search can be viewed as a special case of DFS, and it is also not optimal even if ℓ>d. 4. Uniform-cost Search Algorithm:Uniform-cost search is a searching algorithm used for traversing a weighted tree or graph. This algorithm comes into play when a different cost is available for each edge. The primary goal of the uniform-cost search is to find a path to the goal node which has the lowest cumulative cost. Uniform-cost search expands nodes according to their path costs form the root node. It can be used to solve any graph/tree where the optimal cost is in demand. A uniform-cost search algorithm is implemented by the priority queue. It gives maximum priority to the lowest cumulative cost. Uniform cost search is equivalent to BFS algorithm if the path cost of all edges is the same. Advantages:
Disadvantages:
Example: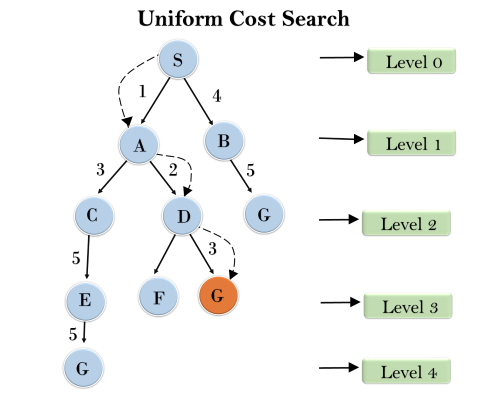
Completeness: Uniform-cost search is complete, such as if there is a solution, UCS will find it. Time Complexity: Let C* is Cost of the optimal solution, and ε is each step to get closer to the goal node. Then the number of steps is = C*/ε+1. Here we have taken +1, as we start from state 0 and end to C*/ε. Hence, the worst-case time complexity of Uniform-cost search isO(b1 + [C*/ε])/. Space Complexity: The same logic is for space complexity so, the worst-case space complexity of Uniform-cost search is O(b1 + [C*/ε]). Optimal: Uniform-cost search is always optimal as it only selects a path with the lowest path cost. 5. Iterative deepeningdepth-first Search:The iterative deepening algorithm is a combination of DFS and BFS algorithms. This search algorithm finds out the best depth limit and does it by gradually increasing the limit until a goal is found. This algorithm performs depth-first search up to a certain "depth limit", and it keeps increasing the depth limit after each iteration until the goal node is found. This Search algorithm combines the benefits of Breadth-first search's fast search and depth-first search's memory efficiency. The iterative search algorithm is useful uninformed search when search space is large, and depth of goal node is unknown. Advantages:
Disadvantages:
Example:Following tree structure is showing the iterative deepening depth-first search. IDDFS algorithm performs various iterations until it does not find the goal node. The iteration performed by the algorithm is given as: 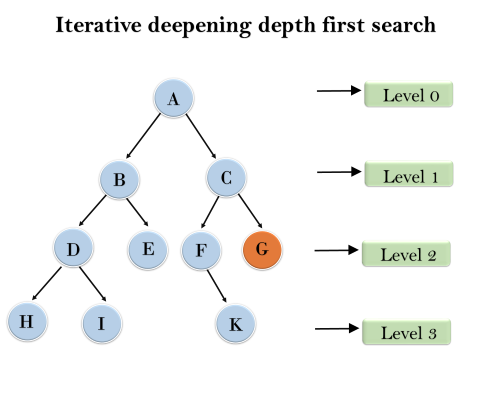
1'st Iteration-----> A Completeness: This algorithm is complete is ifthe branching factor is finite. Time Complexity: Let's suppose b is the branching factor and depth is d then the worst-case time complexity is O(bd). Space Complexity: The space complexity of IDDFS will be O(bd). Optimal: IDDFS algorithm is optimal if path cost is a non- decreasing function of the depth of the node. 6. Bidirectional Search Algorithm:Bidirectional search algorithm runs two simultaneous searches, one form initial state called as forward-search and other from goal node called as backward-search, to find the goal node. Bidirectional search replaces one single search graph with two small subgraphs in which one starts the search from an initial vertex and other starts from goal vertex. The search stops when these two graphs intersect each other. Bidirectional search can use search techniques such as BFS, DFS, DLS, etc. Advantages:
Disadvantages:
Example:In the below search tree, bidirectional search algorithm is applied. This algorithm divides one graph/tree into two sub-graphs. It starts traversing from node 1 in the forward direction and starts from goal node 16 in the backward direction. The algorithm terminates at node 9 where two searches meet. 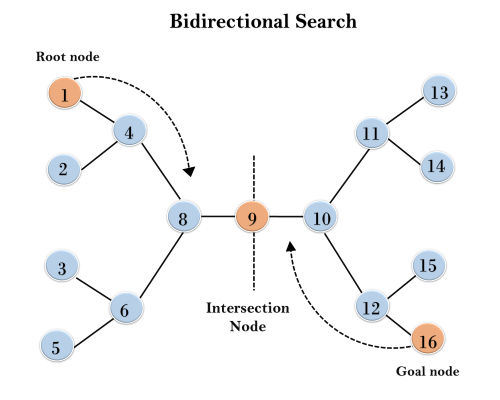
Completeness: Bidirectional Search is complete if we use BFS in both searches. Time Complexity: Time complexity of bidirectional search using BFS is O(bd). Space Complexity: Space complexity of bidirectional search is O(bd). Optimal: Bidirectional search is Optimal.
Next TopicInformed Search Algorithms in AI
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









