Rules of Inference in Artificial intelligenceInference:In artificial intelligence, we need intelligent computers which can create new logic from old logic or by evidence, so generating the conclusions from evidence and facts is termed as Inference. Inference rules:Inference rules are the templates for generating valid arguments. Inference rules are applied to derive proofs in artificial intelligence, and the proof is a sequence of the conclusion that leads to the desired goal. In inference rules, the implication among all the connectives plays an important role. Following are some terminologies related to inference rules:
From the above term some of the compound statements are equivalent to each other, which we can prove using truth table: 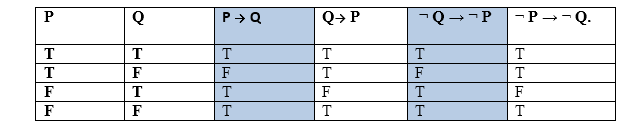
Hence from the above truth table, we can prove that P → Q is equivalent to ¬ Q → ¬ P, and Q→ P is equivalent to ¬ P → ¬ Q. Types of Inference rules:1. Modus Ponens:The Modus Ponens rule is one of the most important rules of inference, and it states that if P and P → Q is true, then we can infer that Q will be true. It can be represented as: 
Example: Statement-1: "If I am sleepy then I go to bed" ==> P→ Q Proof by Truth table: 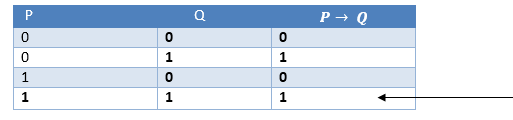
2. Modus Tollens:The Modus Tollens rule state that if P→ Q is true and ¬ Q is true, then ¬ P will also true. It can be represented as: 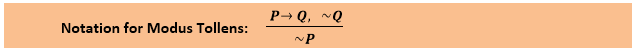
Statement-1: "If I am sleepy then I go to bed" ==> P→ Q Proof by Truth table: 
3. Hypothetical Syllogism:The Hypothetical Syllogism rule state that if P→R is true whenever P→Q is true, and Q→R is true. It can be represented as the following notation: Example: Statement-1: If you have my home key then you can unlock my home. P→Q Proof by truth table: 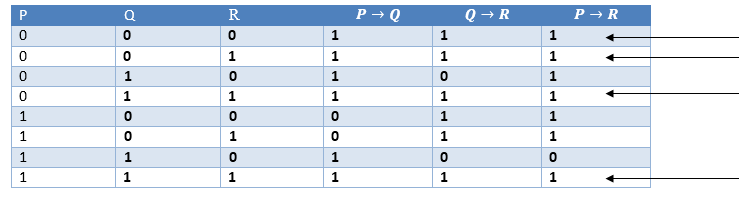
4. Disjunctive Syllogism:The Disjunctive syllogism rule state that if P∨Q is true, and ¬P is true, then Q will be true. It can be represented as: 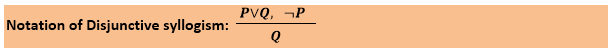
Example: Statement-1: Today is Sunday or Monday. ==>P∨Q Proof by truth-table: 
5. Addition:The Addition rule is one the common inference rule, and it states that If P is true, then P∨Q will be true. 
Example: Statement: I have a vanilla ice-cream. ==> P Proof by Truth-Table: 
6. Simplification:The simplification rule state that if P∧ Q is true, then Q or P will also be true. It can be represented as: 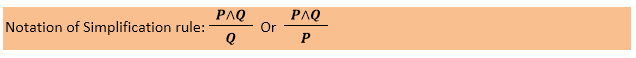
Proof by Truth-Table: 
7. Resolution:The Resolution rule state that if P∨Q and ¬ P∧R is true, then Q∨R will also be true. It can be represented as 
Proof by Truth-Table: 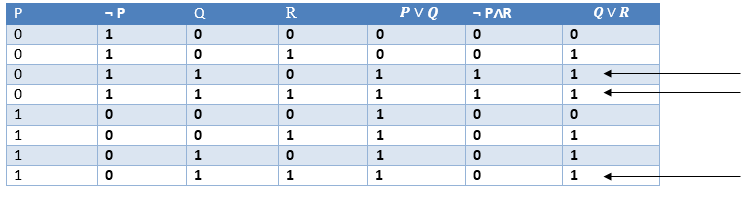
Next TopicThe Wumpus world
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









