Mini-Max Algorithm in Artificial Intelligence
- Mini-max algorithm is a recursive or backtracking algorithm which is used in decision-making and game theory. It provides an optimal move for the player assuming that opponent is also playing optimally.
- Mini-Max algorithm uses recursion to search through the game-tree.
- Min-Max algorithm is mostly used for game playing in AI. Such as Chess, Checkers, tic-tac-toe, go, and various tow-players game. This Algorithm computes the minimax decision for the current state.
- In this algorithm two players play the game, one is called MAX and other is called MIN.
- Both the players fight it as the opponent player gets the minimum benefit while they get the maximum benefit.
- Both Players of the game are opponent of each other, where MAX will select the maximized value and MIN will select the minimized value.
- The minimax algorithm performs a depth-first search algorithm for the exploration of the complete game tree.
- The minimax algorithm proceeds all the way down to the terminal node of the tree, then backtrack the tree as the recursion.
Pseudo-code for MinMax Algorithm:
Initial call:
Minimax(node, 3, true)
Working of Min-Max Algorithm:
- The working of the minimax algorithm can be easily described using an example. Below we have taken an example of game-tree which is representing the two-player game.
- In this example, there are two players one is called Maximizer and other is called Minimizer.
- Maximizer will try to get the Maximum possible score, and Minimizer will try to get the minimum possible score.
- This algorithm applies DFS, so in this game-tree, we have to go all the way through the leaves to reach the terminal nodes.
- At the terminal node, the terminal values are given so we will compare those value and backtrack the tree until the initial state occurs. Following are the main steps involved in solving the two-player game tree:
Step-1: In the first step, the algorithm generates the entire game-tree and apply the utility function to get the utility values for the terminal states. In the below tree diagram, let's take A is the initial state of the tree. Suppose maximizer takes first turn which has worst-case initial value =- infinity, and minimizer will take next turn which has worst-case initial value = +infinity.
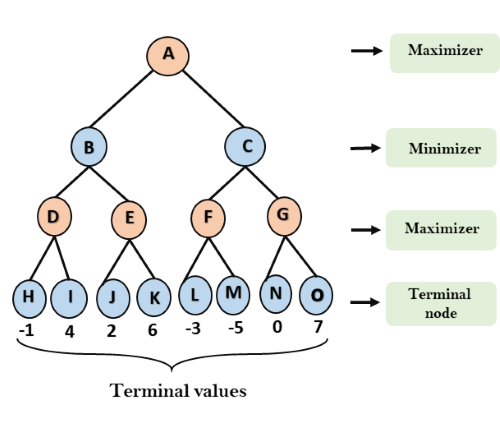
Step 2: Now, first we find the utilities value for the Maximizer, its initial value is -∞, so we will compare each value in terminal state with initial value of Maximizer and determines the higher nodes values. It will find the maximum among the all.
- For node D max(-1,- -∞) => max(-1,4)= 4
- For Node E max(2, -∞) => max(2, 6)= 6
- For Node F max(-3, -∞) => max(-3,-5) = -3
- For node G max(0, -∞) = max(0, 7) = 7
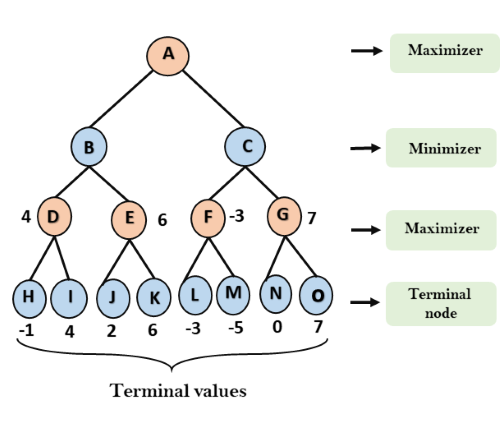
Step 3: In the next step, it's a turn for minimizer, so it will compare all nodes value with +∞, and will find the 3rd layer node values.
- For node B= min(4,6) = 4
- For node C= min (-3, 7) = -3
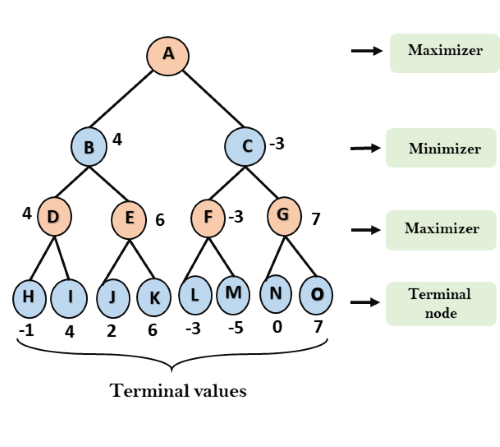
Step 4: Now it's a turn for Maximizer, and it will again choose the maximum of all nodes value and find the maximum value for the root node. In this game tree, there are only 4 layers, hence we reach immediately to the root node, but in real games, there will be more than 4 layers.
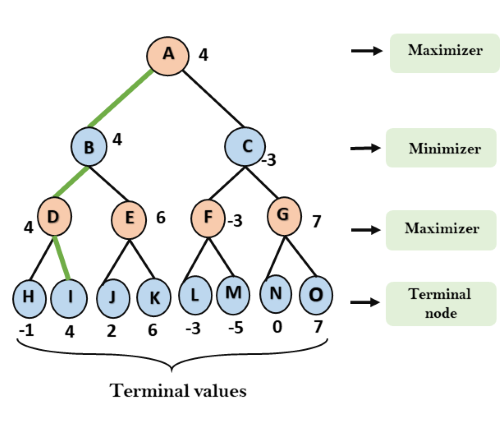
That was the complete workflow of the minimax two player game.
Properties of Mini-Max algorithm:
- Complete- Min-Max algorithm is Complete. It will definitely find a solution (if exist), in the finite search tree.
- Optimal- Min-Max algorithm is optimal if both opponents are playing optimally.
- Time complexity- As it performs DFS for the game-tree, so the time complexity of Min-Max algorithm is O(bm), where b is branching factor of the game-tree, and m is the maximum depth of the tree.
- Space Complexity- Space complexity of Mini-max algorithm is also similar to DFS which is O(bm).
Limitation of the minimax Algorithm:
The main drawback of the minimax algorithm is that it gets really slow for complex games such as Chess, go, etc. This type of games has a huge branching factor, and the player has lots of choices to decide. This limitation of the minimax algorithm can be improved from alpha-beta pruning which we have discussed in the next topic.
|




 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now









