Arithmetic Pipeline

Arithmetic Pipelines are mostly used in high-speed computers. They are used to implement floating-point operations, multiplication of fixed-point numbers, and similar computations encountered in scientific problems.

To understand the concepts of arithmetic pipeline in a more convenient way, let us consider an example of a pipeline unit for floating-point addition and subtraction.

The inputs to the floating-point adder pipeline are two normalized floating-point binary numbers defined as:

    X = A * 2a = 0.9504 * 103
    Y = B * 2b = 0.8200 * 102

Where A and B are two fractions that represent the mantissa and a and b are the exponents.

The combined operation of floating-point addition and subtraction is divided into four segments. Each segment contains the corresponding suboperation to be performed in the given pipeline. The suboperations that are shown in the four segments are:

1. Compare the exponents by subtraction.
2. Align the mantissas.
3. Add or subtract the mantissas.
4. Normalize the result.

We will discuss each suboperation in a more detailed manner later in this section.

The following block diagram represents the suboperations performed in each segment of the pipeline.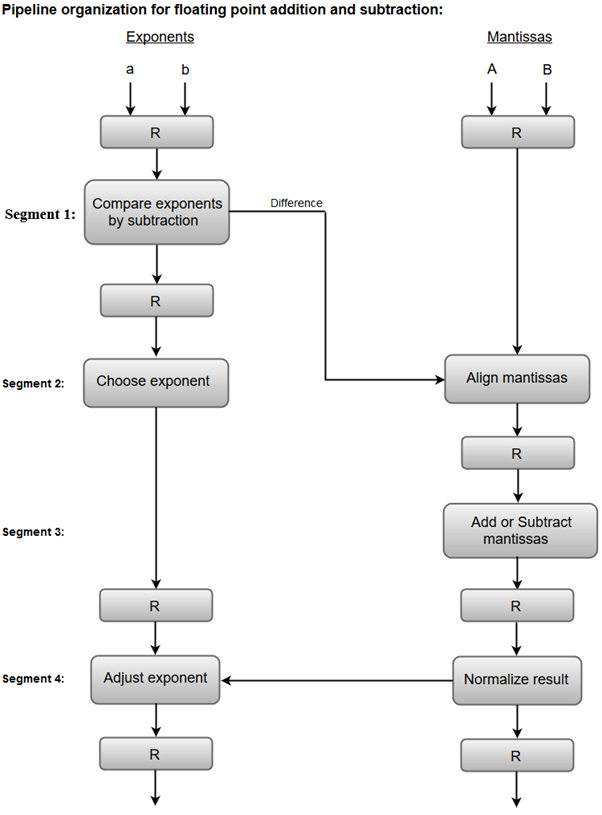

Note: Registers are placed after each suboperation to store the intermediate results.

1. Compare exponents by subtraction:

The exponents are compared by subtracting them to determine their difference. The larger exponent is chosen as the exponent of the result.

The difference of the exponents, i.e., 3 - 2 = 1 determines how many times the mantissa associated with the smaller exponent must be shifted to the right.

2. Align the mantissas:

The mantissa associated with the smaller exponent is shifted according to the difference of exponents determined in segment one.

	X = 0.9504 *  103
	Y = 0.08200 * 103

3. Add mantissas:

The two mantissas are added in segment three.

Z = X + Y = 1.0324 * 103

4. Normalize the result:

After normalization, the result is written as:

Z = 0.1324 * 104