Types of Operands in Computer OrganizationComputer instruction is a binary code that determines the micro-operations in a sequence for a computer. They are saved in the memory along with the information. Each computer has its specific group of instructions. They can be categorized into two elements as Operation codes (Opcodes) and Address. Opcodes specify the operation for specific instructions, and an address determines the registers or the areas used for that operation. Operands are definite elements of computer instruction that show what information is to be operated on. The most important general categories of data are
In many cases, some calculation must be performed on the operand reference to determine the main or virtual memory address. In this context, addresses can be considered to be unsigned integers. Other common data types are numbers, characters, and logical data, and each of these is briefly described below. Some machines define specialized data types or data structures. For example, machine operations may operate directly on a list or a string of characters. 
AddressesAddresses are nothing but a form of data. Here some calculations must be performed on the operand reference in an instruction, which is to determine the physical address of an instruction. NumbersAll machine languages include numeric data types. Even in non-numeric data processing, numbers are needed to act as counters, field widths, etc. An important difference between numbers used in ordinary mathematics and numbers stored in a computer is that the latter is limited. Thus, the programmer is faced with understanding the consequences of rounding, overflow and underflow. Here are the three types of numerical data in computers, such as: 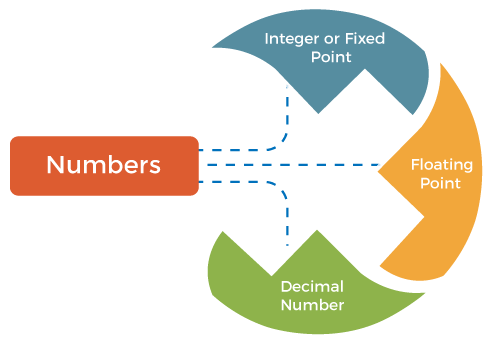
1. Integer or fixed point: Fixed point representation is used to store integers, the positive and negative whole numbers (… -3, -2, -1, 0, 1, 2, 3, …). However, the programmer assigns a radix point location to each number and tracks the radix point through every operation. High-level programs, such as C and BASIC usually allocate 16 bits to store each integer. Each fixed point binary number has three important parameters that describe it:
2. Floating point: A Floating Point number usually has a decimal point, which means 0, 3.14, 6.5, and-125.5 are Floating Point The term floating point is derived from the fact that there is no fixed number of digits before and after the decimal point, which means the decimal point can float. There are also representations in which the number of digits before and after the decimal point is set, called fixed-point representations. In general, floating-point representations are slower and less accurate than fixed-point representations, but they can handle a larger range of numbers. 3. Decimal number: The decimals are an extension of our number system. We also know that decimals can be considered fractions with 10, 100, 1000, etc. The numbers expressed in the decimal form are called decimal numbersor decimals. For example:1, 4.09, 13.83, etc. A decimal number has two parts, and a dot separates these parts (.) called the decimal point.
CharactersA common form of data is text or character strings. While textual data are most convenient for humans. But computers work in binary. So, all characters, whether letters, punctuation or digits, are stored as binary numbers. All of the characters that a computer can use are called character sets. Here are the two common standards, such as:
ASCII uses seven bits, giving a character set of 128 characters. The characters are represented in a table called the ASCII table. The 128 characters include:
We can say that the letter 'A' is the first letter of the alphabet; 'B' is the second, and so on, all the way up to 'Z', which is the 26th letter. In ASCII, each character has its own assigned number. Denary, binary and hexadecimal representations of ASCII characters are shown in the below table.
A is represented by the denary number 65 (binary 1000001, hexadecimal 41), B by 66 (binary 1000010, hexadecimal 42) and so on up to Z, which is represented by the denary number 90 (binary 1011010, hexadecimal 5A). Similarly, lower-case letters start at denary 97 (binary 1100001, hexadecimal 61) and end at denary 122 (binary 1111010, hexadecimal 7A). When data is stored or transmitted, its ASCII or Unicode number is used, not the character itself. For example, the word "Computer" would be represented as: 1000011 1101111 1101101 1110000 1110101 1110100 1100101 1110010 On the other hand, IRA is also widely used outside the United States. A unique 7-bit pattern represents each character in this code. Thus, 128 different characters can be represented, and more than necessary to represent printable characters, and some of the patterns represent control characters. Some control characters control the printing of characters on a page, and others are concerned with communications procedures. IRA-encoded characters are always stored and transmitted using 8 bits per character. The 8 bit may be set to 0 or used as a parity bit for error detection. In the latter case, the bit is set such that the total number of binary 1s in each octet is always odd (odd parity) or always even (even parity). Logical dataNormally, each word or other addressable unit (byte, half-word, and so on) is treated as a single unit of data. Sometimes, it is useful to consider an n-bit unit consisting of 1-bit items of data, each item having the value 0 or 1. When data are viewed this way, they are considered to be logical data. The Boolean data can only represent two values: true or false. Although only two values are possible, they are rarely implemented as a single binary digit for efficiency reasons. Many programming languages do not have an explicit Boolean type, instead of interpreting 0 as false and other values as true. Boolean data refers to the logical structure of how the language is interpreted to the machine language. In this case, a Boolean 0 refers to the logic False, and true is always a non zero, especially one known as Boolean 1. There are two advantages to the bit-oriented view:
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










