Examples of Boolean algebra simplifications using the map method1. F(x,y,z) = Σ (2,3,4,5) First, 1 is marked in each min-term that represents the function. Hence, 010, 011, 100, 101 are marked with 1's. Subsequently, we have to find possible adjacent squares. These are indicated in the map by two rectangles, each enclosing two 1's. 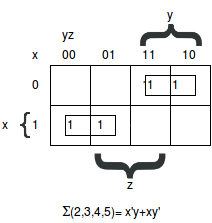
The upper right rectangle represents the area enclosed by x'y. The lower left rectangle represents the product term xy'. The sum of these two terms gives the simplified expression: F= x'y+ xy' Note: There are cases where two squares in the map are considered to be adjacent even though they do not touch each other. In the figure below, m0 is adjacent to m2 and m4 is adjacent to m6 because the min-terms differ by one variable.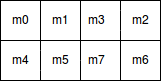
Algebraically verification: m0+m2 = x'y'z'+ x'yz'= x'z'(y'+y) = x'z' m4+m6 = xy'z' + xyz'= xz' + (y'+y) = xz' 2. F(x,y,z) = Σ(3,4,6,7) 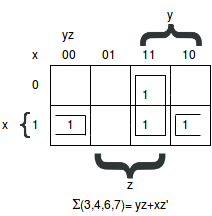
As you can see, there are four squares marked with 1's, one for each min-term of the function. The other two adjacent squares are combined in the third column to give a two-literal term yz. The remaining two squares with 1's are shown in the above diagram with their values enclosed in half rectangles. When these two half rectangles are combined, it yields two literal term xz'. The simplified function becomes F= yz+xz'.
Next TopicCombinational Circuits
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









