Correlation Analysis in Data MiningCorrelation analysis is a statistical method used to measure the strength of the linear relationship between two variables and compute their association. Correlation analysis calculates the level of change in one variable due to the change in the other. A high correlation points to a strong relationship between the two variables, while a low correlation means that the variables are weakly related. Researchers use correlation analysis to analyze quantitative data collected through research methods like surveys and live polls for market research. They try to identify relationships, patterns, significant connections, and trends between two variables or datasets. There is a positive correlation between two variables when an increase in one variable leads to an increase in the other. On the other hand, a negative correlation means that when one variable increases, the other decreases and vice-versa. Correlation is a bivariate analysis that measures the strength of association between two variables and the direction of the relationship. In terms of the strength of the relationship, the correlation coefficient's value varies between +1 and -1. A value of ± 1 indicates a perfect degree of association between the two variables. As the correlation coefficient value goes towards 0, the relationship between the two variables will be weaker. The coefficient sign indicates the direction of the relationship; a + sign indicates a positive relationship, and a - sign indicates a negative relationship. Why Correlation Analysis is ImportantCorrelation analysis can reveal meaningful relationships between different metrics or groups of metrics. Information about those connections can provide new insights and reveal interdependencies, even if the metrics come from different parts of the business. Suppose there is a strong correlation between two variables or metrics, and one of them is being observed acting in a particular way. In that case, you can conclude that the other one is also being affected similarly. This helps group related metrics together to reduce the need for individual data processing. Types of Correlation Analysis in Data MiningUsually, in statistics, we measure four types of correlations: Pearson correlation, Kendall rank correlation, Spearman correlation, and the Point-Biserial correlation. 1. Pearson r correlation Pearson r correlation is the most widely used correlation statistic to measure the degree of the relationship between linearly related variables. For example, in the stock market, if we want to measure how two stocks are related to each other, Pearson r correlation is used to measure the degree of relationship between the two. The point-biserial correlation is conducted with the Pearson correlation formula, except that one of the variables is dichotomous. The following formula is used to calculate the Pearson r correlation: 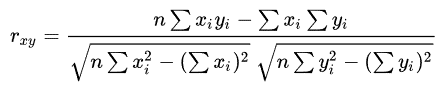
rxy= Pearson r correlation coefficient between x and y n= number of observations xi = value of x (for ith observation) yi= value of y (for ith observation) 2. Kendall rank correlation Kendall rank correlation is a non-parametric test that measures the strength of dependence between two variables. Considering two samples, a and b, where each sample size is n, we know that the total number of pairings with a b is n(n-1)/2. The following formula is used to calculate the value of Kendall rank correlation: 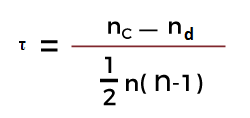
Nc= number of concordant Nd= Number of discordant 3. Spearman rank correlation Spearman rank correlation is a non-parametric test that is used to measure the degree of association between two variables. The Spearman rank correlation test does not carry any assumptions about the data distribution. It is the appropriate correlation analysis when the variables are measured on an at least ordinal scale. This coefficient requires a table of data that displays the raw data, its ranks, and the difference between the two ranks. This squared difference between the two ranks will be shown on a scatter graph, which will indicate whether there is a positive, negative, or no correlation between the two variables. The constraint that this coefficient works under is -1 ≤ r ≤ +1, where a result of 0 would mean that there was no relation between the data whatsoever. The following formula is used to calculate the Spearman rank correlation: 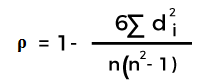
ρ= Spearman rank correlation di= the difference between the ranks of corresponding variables n= number of observations When to Use These MethodsThe two methods outlined above will be used according to whether there are parameters associated with the data gathered. The two terms to watch out for are:
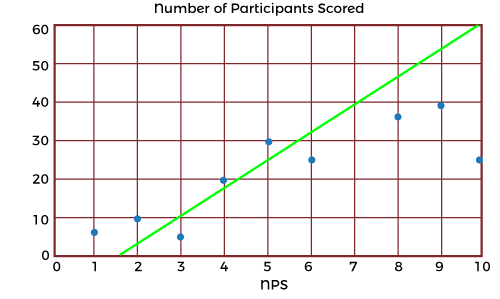
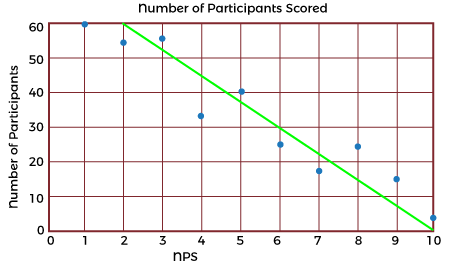
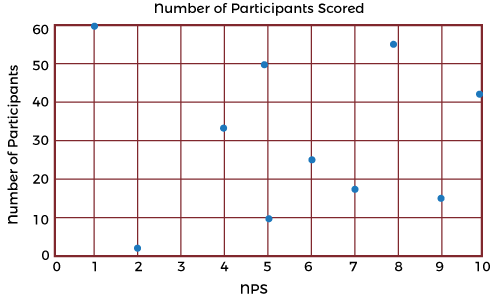
In cases when both are applicable, statisticians recommend using the parametric methods such as Pearson's Coefficient because they tend to be more precise. But that doesn't mean discounting the non-parametric methods if there isn't enough data or a more specified accurate result is needed. Interpreting ResultsTypically, the best way to gain a generalized but more immediate interpretation of the results of a set of data is to visualize it on a scatter graph such as these:
Outliers or anomalies must be accounted for in both correlation coefficients. Using a scatter graph is the easiest way of identifying any anomalies that may have occurred. Running the correlation analysis twice (with and without anomalies) is a great way to assess the strength of the influence of the anomalies on the analysis. Spearman's Rank coefficient may be used if anomalies are present instead of Pearson's Coefficient, as this formula is extremely robust against anomalies due to the ranking system used. Benefits of Correlation AnalysisHere are the following benefits of correlation analysis, such as: 1. Reduce Time to Detection In anomaly detection, working with many metrics and surfacing correlated anomalous metrics helps draw relationships that reduce time to detection (TTD) and support shortened time to remediation (TTR). As data-driven decision-making has become the norm, early and robust detection of anomalies is critical in every industry domain, as delayed detection adversely impacts customer experience and revenue. 2. Reduce Alert Fatigue Another important benefit of correlation analysis in anomaly detection is reducing alert fatigue by filtering irrelevant anomalies (based on the correlation) and grouping correlated anomalies into a single alert. Alert storms and false positives are significant challenges organizations face - getting hundreds, even thousands of separate alerts from multiple systems when many of them stem from the same incident. 3. Reduce Costs Correlation analysis helps significantly reduce the costs associated with the time spent investigating meaningless or duplicative alerts. In addition, the time saved can be spent on more strategic initiatives that add value to the organization. Example Use Cases for Correlation AnalysisMarketing professionals use correlation analysis to evaluate the efficiency of a campaign by monitoring and testing customers' reactions to different marketing tactics. In this way, they can better understand and serve their customers. Financial planners assess the correlation of an individual stock to an index such as the S&P 500 to determine if adding the stock to an investment portfolio might increase the portfolio's systematic risk. For data scientists and those tasked with monitoring data, correlation analysis is incredibly valuable for root cause analysis and reduces time to detection (TTD) and remediation (TTR). Two unusual events or anomalies happening simultaneously/rate can help pinpoint an underlying cause of a problem. The organization will incur a lower cost of experiencing a problem if it can be understood and fixed sooner. Technical support teams can reduce the number of alerts they must respond to by filtering irrelevant anomalies and grouping correlated anomalies into a single alert. Tools such as Security Information and Event Management (SIEM) systems automatically facilitate incident response. Does Correlation Imply Causation?While correlation analysis techniques may identify a significant relationship, correlation does not imply causation. The analysis cannot determine the cause, nor should this conclusion be attempted. The significant relationship implies more understanding and extraneous or underlying factors that should be explored further to search for a cause. While a causal relationship may exist, any researcher would be remiss in using the correlation results to prove this existence. The cause of any relationship discovered through the correlation analysis is for the researcher to determine through other means of statistical analysis, such as the coefficient of determination analysis. However, correlation analysis can provide a great amount of value; for example, the value of the dependency or the variables can be estimated, which can help firms estimate the cost and sale of a product or service. In essence, the uses for and applications of correlation-based statistical analyses allow researchers to identify which aspects and variables are dependent on each other, which can generate actionable insights as they are or starting points for further investigations and deeper insights.
Next TopicData Mining Services
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share