Data Mining Bayesian ClassifiersIn numerous applications, the connection between the attribute set and the class variable is non- deterministic. In other words, we can say the class label of a test record cant be assumed with certainty even though its attribute set is the same as some of the training examples. These circumstances may emerge due to the noisy data or the presence of certain confusing factors that influence classification, but it is not included in the analysis. For example, consider the task of predicting the occurrence of whether an individual is at risk for liver illness based on individuals eating habits and working efficiency. Although most people who eat healthly and exercise consistently having less probability of occurrence of liver disease, they may still do so due to other factors. For example, due to consumption of the high-calorie street foods and alcohol abuse. Determining whether an individual's eating routine is healthy or the workout efficiency is sufficient is also subject to analysis, which in turn may introduce vulnerabilities into the leaning issue. Bayesian classification uses Bayes theorem to predict the occurrence of any event. Bayesian classifiers are the statistical classifiers with the Bayesian probability understandings. The theory expresses how a level of belief, expressed as a probability. Bayes theorem came into existence after Thomas Bayes, who first utilized conditional probability to provide an algorithm that uses evidence to calculate limits on an unknown parameter. Bayes's theorem is expressed mathematically by the following equation that is given below. 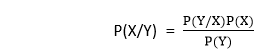
Where X and Y are the events and P (Y) ≠ 0 P(X/Y) is a conditional probability that describes the occurrence of event X is given that Y is true. P(Y/X) is a conditional probability that describes the occurrence of event Y is given that X is true. P(X) and P(Y) are the probabilities of observing X and Y independently of each other. This is known as the marginal probability. Bayesian interpretation: In the Bayesian interpretation, probability determines a "degree of belief." Bayes theorem connects the degree of belief in a hypothesis before and after accounting for evidence. For example, Lets us consider an example of the coin. If we toss a coin, then we get either heads or tails, and the percent of occurrence of either heads and tails is 50%. If the coin is flipped numbers of times, and the outcomes are observed, the degree of belief may rise, fall, or remain the same depending on the outcomes. For proposition X and evidence Y,
Bayes theorem can be derived from the conditional probability: 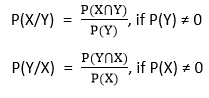
Where P (X⋂Y) is the joint probability of both X and Y being true, because 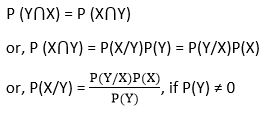
Bayesian network: A Bayesian Network falls under the classification of Probabilistic Graphical Modelling (PGM) procedure that is utilized to compute uncertainties by utilizing the probability concept. Generally known as Belief Networks, Bayesian Networks are used to show uncertainties using Directed Acyclic Graphs (DAG) A Directed Acyclic Graph is used to show a Bayesian Network, and like some other statistical graph, a DAG consists of a set of nodes and links, where the links signify the connection between the nodes. 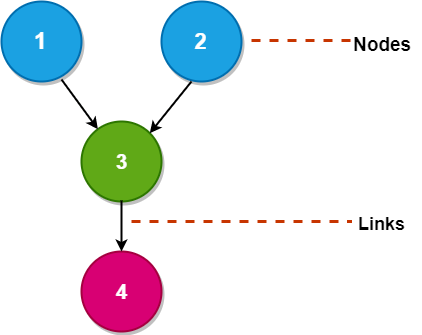
The nodes here represent random variables, and the edges define the relationship between these variables. A DAG models the uncertainty of an event taking place based on the Conditional Probability Distribution (CDP) of each random variable. A Conditional Probability Table (CPT) is used to represent the CPD of each variable in a network.
Next TopicData Mining World Wide Web
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share





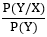 represents the supports Y provides for X.
represents the supports Y provides for X.




