QUESTIONS TO IDENTIFY NORMAL FORM

To solve the question to identify normal form, we must understand its definitions of BCNF, 3 NF, and 2NF:

Definition of 2NF: No non-prime attribute should be partially dependent on Candidate Key. i.e. there should not be a partial dependency from X → Y.

Definition of 3NF: First, it should be in 2NF and if there exists a non-trivial dependency between two sets of attributes X and Y such that X → Y (i.e. Y is not a subset of X) then

1. Either X is Super Key
2. Or Y is a prime attribute.

Definition of BCNF: First, it should be in 3NF and if there exists a non-trivial dependency between two sets of attributes X and Y such that X → Y (i.e., Y is not a subset of X) then

1. X is Super Key

NOTE: If a table is in BCNF then it is in 3NF, 2NF, and 1NF, similarly if the table is in 3NF Then it is in 2NF and 1NF. Hence, we can say that if a table is in the higher normal form then by default it is in lower normal form.

Question 1: Given a relation R( P, Q, R, S, T, U, V, W, X) and Functional Dependency set FD = { PQ → R, QS → TU, PS → VW, and P → X }, determine whether the given R is in which normal form?

Solution: Let us construct an arrow diagram on R using FD to calculate the candidate key.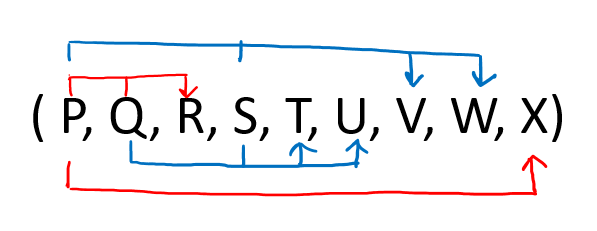

From the above arrow diagram on R, we can see that an attribute PQS is not determined by any of the given FD, hence PQS will be the integral part of the Candidate key, i.e. no matter what will be the candidate key, and how many will be the candidate key, but all will have PQS compulsory attribute.

Let us calculate the closure of PQS

PQS + = P Q R S T U X V W (from the closure method we studied earlier)

Since the closure of PQS contains all the attributes of R, hence PQS is Candidate Key

From the definition of Candidate Key (Candidate Key is a Super Key whose no proper subset is a Super key)

Since all key will have PQS as an integral part, and we have proved that PQS is Candidate Key, Therefore, any superset of PQS will be Super Key but not a Candidate key.

Hence there will be only one candidate key PQS

Since R has 9 attributes: - P, Q, R, S, T, U, V, W, X, and Candidate Key is PQS, Therefore, prime attributes (part of candidate key) are P Q and S while a non-prime attribute is R T U V W X

Given FD are { PQ → R, QS → TU, PS → VW, and P → X } and Super Key / Candidate Key is PQS

NOTE: To solve such questions, we apply reverse engineering, i.e. 1^st check BCNF, if not then 3NF, if not then 2NF, and so on.

1. FD: PQ → R does not satisfy the definition of BCNF, as PQ is not Super Key, hence the table is not in BCNF (because if one dependency fails, all fails) now we check the same FD for 3NF.
2. FD: PQ → R even does not satisfy the definition of 3NF, as PQ is not Super Key or R is not a prime attribute, hence table is not in 3NF also (because if one dependency fails, all fails) now we check same FD for 2NF
3. FD: PQ → R even does not satisfy the definition of 2NF, as PQ is not Super Key and R which is not prime attribute depending on part of the key (partial dependency), hence table is not in 2NF also (because if one dependency fails, all fails).

Hence from the above three statements, we can say that table R ( P, Q, R, S, T, U, V, W, X) is in 1NF only.

Question 2: Given a relation R( P, Q, R, S, T, U, V, W ) and Functional Dependency set FD = { PQ → R, P → ST, Q → U, and U → VW }, determine given R is in which normal form?

Solution: Let us construct an arrow diagram on R using FD to calculate the candidate key.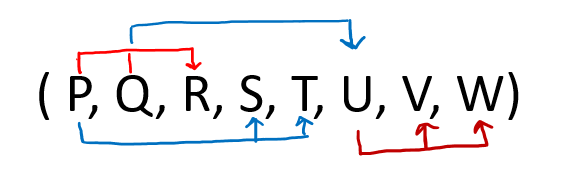

From the above arrow diagram on R, we can see that an attribute PQ is not determined by any of the given FD, hence PQ will be the integral part of the Candidate key, i.e. no matter what will be the candidate key, and how many will be the candidate key, but all will have PQ compulsory attribute.

Let us calculate the closure of PQ

PQ + = P Q R S T U V W (from the closure method we studied earlier)

Since the closure of PQ contains all the attributes of R, hence PQ is Candidate Key

From the definition of Candidate Key (Candidate Key is a Super Key whose no proper subset is a Super key)

Since all key will have PQ as an integral part, and we have proved that PQ is Candidate Key, Therefore, any superset of PQ will be Super Key but not Candidate key.

Hence there will be only one candidate key PQ

Since R has 8 attributes: - P, Q, R, S, T, U, V, W and Candidate Key is PQ. Therefore, prime attribute (part of candidate key) are P and Q while a non-prime attribute is R S T U V W

Given FD are { PQ → R, P → ST, Q → U, and U → VW } and Super Key / Candidate Key is PQ

NOTE: To solve such questions, we apply reverse engineering, i.e. 1^st check BCNF, if not then 3NF, if not then 2NF, and so on.

1. FD: PQ → R satisfies the definition of BCNF, as PQ is Super Key, hence no need to check it for further normal forms, as it satisfies the highest one. Now we check another dependency in a reverse engineering manner.
2. FD: P → ST does not satisfy the definition of BCNF, as P is not Super Key, hence table is not in BCNF (because if one dependency fails, all fails) now we check the same FD for 3NF.
3. FD: P → ST even does not satisfy the definition of 3NF, as P is not Super Key or S T is not a prime attribute, hence table is not in 3NF also (because if one dependency fails, all fails) now we check same FD for 2NF.
4. FD: P → ST even does not satisfy the definition of 2NF, as P is not Super Key and S T which is not prime attribute depending on part of the key (partial dependency), hence table is not in 2NF also (because if one dependency fails, all fails).

Hence from the above three statements b, c, and d we can say that table R ( P, Q, R, S, T, U, V, W, ) is in 1NF only.

Question 3: Given a relation R( P, Q, R, S, T, U ) and Functional Dependency set FD = { PQ → R, SR→ PT, T → U }, determine given R is in which normal form?

Solution: Let us construct an arrow diagram on R using FD to calculate the candidate key.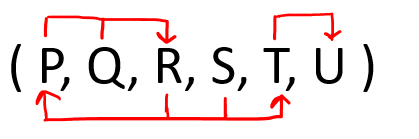

From the above arrow diagram on R, we can see that an attribute QS is not determined by any of the given FD, hence QS will be the integral part of the Candidate key, i.e. no matter what will be the candidate key, and how many will be the candidate key, but all will have QS compulsory attribute.

Let us calculate the closure of QS

QS + = QS (from the closure method we studied earlier)

Since closure QS does not contain all the attributes of R, hence QS is not the Candidate key.

On making a combination of QS with another attribute, we found that PQS and RQS determine all the attributes of R, hence PQS and RQS are candidate keys of R.

Since R has 6 attributes: - P, Q, R, S, T, U and Candidate Key is PQS and RQS, Therefore, prime attributes (part of candidate key) are P Q R and S while a non-prime attribute is T U

Given FD are { PQ → R, SR→ PT, T → U } and Super Key / Candidate Key is PQS and RQS

NOTE: To solve such questions, we apply reverse engineering, i.e. 1^st check BCNF, if not then 3NF, if not then 2NF, and so on.

1. FD: PQ → R does not satisfy the definition of BCNF, as PQ is not Super Key, hence table is not in BCNF (because if one dependency fails, all fails) now we check the same FD for 3NF
2. FD: PQ → R satisfies the definition of 3NF, even though PQ is not Super Key but R is attributed, hence the table is in 3NF now we check other FD's using reverse engineering process.
3. FD: SR → PT does not satisfy the definition of 3NF, as SR is not Super Key or P T is not prime attribute (as P is prime but the combination should be prime attribute), hence table is not in 3NF (because if one dependency fails, all fails). now we check the same FD for 2NF
4. FD: SR → PT does not satisfy the definition of 2NF, as SR is not Super Key or P T which is not prime attribute depending on part of the key (partial dependency), hence table is not in 2NF also (because if one dependency fails, all fails).

Hence from the above two statements c and d, we can say that table R ( P, Q, R, S, T, U) is in 1NF only.

Question 4: Given a relation R( P, Q, R, S, T) and Functional Dependency set FD = { QR → PST, S → Q }, determine given R is in which normal form?

Solution: Let us construct an arrow diagram on R using FD to calculate the candidate key.

From the above arrow diagram on R, we can see that an attribute R is not determined by any of the given FD, hence R will be the integral part of the Candidate key, i.e. no matter what will be the candidate key, and how many will be the candidate key, but all will have R compulsory attribute.

Let us calculate the closure of R

R + = R (from the closure method we studied earlier)

Since closure R does not contain all the attributes of R, hence R is not Candidate key.

On making a combination of R with another attribute, we found that RS and RQ determine all the attributes of R, hence RS and RQ are candidate keys of R.

Since R has 5 attributes: - P, Q, R, S, T and Candidate Keys are RS and RQ, Therefore prime attributes (part of candidate key) are S Q R while a non-prime attribute is TP

Given FD are { QR → PST, S → Q } and Super Key / Candidate Key is RS and RQ

NOTE: To solve such questions, we apply reverse engineering, i.e. 1^st check BCNF, if not then 3NF, if not then 2NF, and so on.

1. FD: QR → PST satisfies the definition of BCNF, as QR is Super Key, we check other FD for BCNF
2. FD: S → Q does not satisfy the definition of BCNF, as S is not Super Key, hence table is not in BCNF (because if one dependency fails, all fails) now we check the same FD for 3NF
3. FD: S → Q satisfies the definition of 3NF, even though S is not Super Key but Q is the prime attribute, hence the table is in 3NF.

Since there were only two FD's, out of which one ( QR → PST ) satisfy BCNF while the other ( S → Q) satisfy 3NF, hence the highest normal form is 3NF R(P, Q, R, S, T) is in 3NF.

Question 5: Given a relation R( A, B, C) and Functional Dependency set FD = { A → B, B → C, and C → A}, determine given R is in which normal form?

Solution: Let us construct an arrow diagram on R using FD to calculate the candidate key.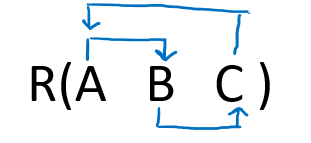

From the above arrow diagram on R, we can see that all the attributes are determined by all the attributes of the given FD, hence we will check all the attributes (i.e., A, B, and C) for candidate keys

Let us calculate the closure of A

A + = ABC (from the closure method we studied earlier)

Since closure A contains all the attributes of R, hence A is the Candidate key.

Let us calculate the closure of B

B + = BAC (from the closure method we studied earlier)

Since closure B contains all the attributes of R, hence B is the Candidate key.

Let us calculate the closure of C

C + = CAB (from the closure method we studied earlier)

Since closure C contains all the attributes of R, hence C is the Candidate key.

Hence three Candidate keys are: A B and C

Since R has 3 attributes: - A B and C, Candidate Keys are A B and C, Therefore, prime attributes (part of candidate key) are A B C while there is no non-prime attribute

Given FD are { A → B, B → C, and C → A } and Super Key / Candidate Key is A B and C

NOTE: To solve such questions, we apply reverse engineering, i.e. 1^st check BCNF, if not then 3NF, if not then 2NF, and so on.

1. FD: A → B satisfy the definition of BCNF, as A is Super Key, we check other FD for BCNF
2. FD: B → C satisfy the definition of BCNF, as B is Super Key, we check other FD for BCNF
3. FD: C à A satisfy the definition of BCNF, as C is Super Key

Since there were only three FD's and all FD: { A → B, B → C and C → A } satisfy BCNF, hence the highest normal form is BCNF.

Therefore R(A, B, C ) is in BCNF.

Conclusion: From the above three examples, we can conclude that the following steps are followed to identify the normal form for a given relational schema.

STEP 1: Calculate the Candidate Key of given R by using an arrow diagram and then using the closure of an attribute on R, such that from the calculated candidate key we can separate the prime attributes and non-prime attributes.

STEP 2: Verify each FD's in the reverse engineering process, i.e. 1st check BCNF, if not then 3NF, if not then 2NF, and so on.

STEP 3: If a table is in BCNF then it is in 3NF, 2NF, and 1NF, similarly if the table is in 3NF THEN it is in 2NF and 1NF. Hence, we can say that if a table is in the higher normal form then by default it is in lower normal form.

STEP 4: Verify first FD with Definition of BCNF (First it should be in 3NF and if there exists a non-trivial dependency between two sets of attributes X and Y such that X → Y (i.e., Y is not a subset of X) then X is Super Key.

STEP 5: If for any FD STEP 5 fails(it signifies that table is not in BCNF), then verify that FD and remaining FD with Definition of 3NF( First it should be in 2NF and if there exist a non-trivial dependency between two sets of attributes X and Y such that X → Y ( i.e. Y is not a subset of X) then X is Super Key or Y is a prime attribute

STEP 6: If for any FD STEP 6 fails (it signifies that table is not in BCNF), then verify that FD and remaining FD with Definition of 2NF (No non-prime attribute should be partially dependent on the key of table).

STEP 7: If for any FD STEP 7 fails (it signifies that table is not in 2NF), hence no need to check it for 1NF, as by default it is in 1NF.

STEP 8: If all the FD's satisfy the definition of BCNF then we can say that given R is in BCNF, if any FD fails for BCNF and that FD and remaining FD satisfy for 3NF then we say R is in 3NF, similarly if any FD fails for 3NF and that FD and remaining FD satisfy for 2NF then we say R is in 2NF, otherwise the table is in 1NF.