Testing of Serializability
Serialization Graph is used to test the Serializability of a schedule.
Assume a schedule S. For S, we construct a graph known as precedence graph. This graph has a pair G = (V, E), where V consists a set of vertices, and E consists a set of edges. The set of vertices is used to contain all the transactions participating in the schedule. The set of edges is used to contain all edges Ti ->Tj for which one of the three conditions holds:
- Create a node Ti → Tj if Ti executes write (Q) before Tj executes read (Q).
- Create a node Ti → Tj if Ti executes read (Q) before Tj executes write (Q).
- Create a node Ti → Tj if Ti executes write (Q) before Tj executes write (Q).
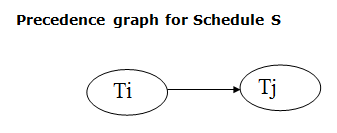
- If a precedence graph contains a single edge Ti → Tj, then all the instructions of Ti are executed before the first instruction of Tj is executed.
- If a precedence graph for schedule S contains a cycle, then S is non-serializable. If the precedence graph has no cycle, then S is known as serializable.
For example:
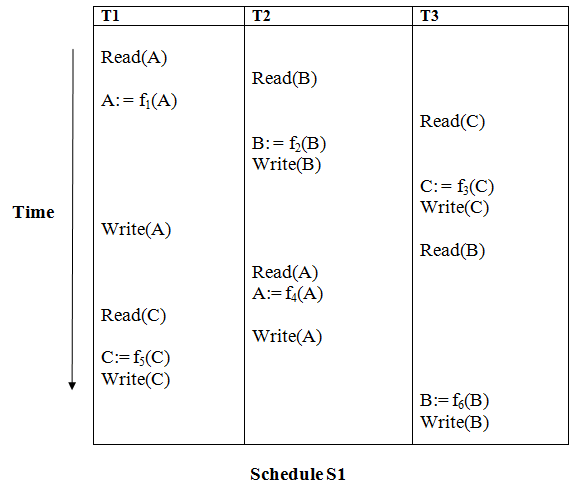
Explanation:
Read(A): In T1, no subsequent writes to A, so no new edges
Read(B): In T2, no subsequent writes to B, so no new edges
Read(C): In T3, no subsequent writes to C, so no new edges
Write(B): B is subsequently read by T3, so add edge T2 → T3
Write(C): C is subsequently read by T1, so add edge T3 → T1
Write(A): A is subsequently read by T2, so add edge T1 → T2
Write(A): In T2, no subsequent reads to A, so no new edges
Write(C): In T1, no subsequent reads to C, so no new edges
Write(B): In T3, no subsequent reads to B, so no new edges
Precedence graph for schedule S1:
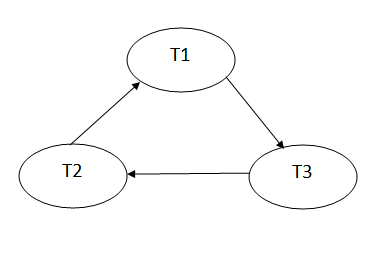
The precedence graph for schedule S1 contains a cycle that's why Schedule S1 is non-serializable.
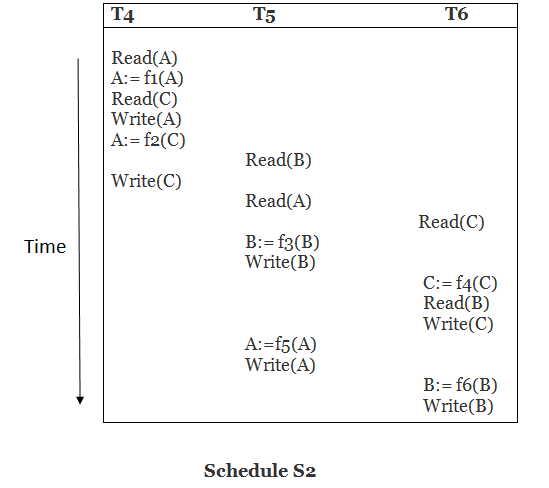
Explanation:
Read(A): In T4,no subsequent writes to A, so no new edges
Read(C): In T4, no subsequent writes to C, so no new edges
Write(A): A is subsequently read by T5, so add edge T4 → T5
Read(B): In T5,no subsequent writes to B, so no new edges
Write(C): C is subsequently read by T6, so add edge T4 → T6
Write(B): A is subsequently read by T6, so add edge T5 → T6
Write(C): In T6, no subsequent reads to C, so no new edges
Write(A): In T5, no subsequent reads to A, so no new edges
Write(B): In T6, no subsequent reads to B, so no new edges
Precedence graph for schedule S2:
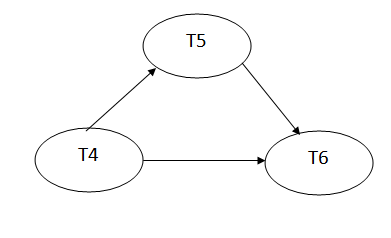
The precedence graph for schedule S2 contains no cycle that's why ScheduleS2 is serializable.
|





 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now









