QUESTIONS ON BOYCE CODD NORMAL FORM

To solve the question on BCNF, we must understand its definitions of BCNF:

Definition: First it should be in 3NF and if there exists a non-trivial dependency between two sets of attributes X and Y such that X → Y (i.e., Y is not a subset of X) then

a) X is Super Key

The relation between 3NF and BCNF is:

All BCNF is 3NF but vice versa may or may not be true.

Question: Given a relation R( X, Y, Z) and Functional Dependency set FD = { XY → Z and Z → Y }, determine whether the given R is in BCNF? If not convert it into BCNF.

Solution: Let us construct an arrow diagram on R using FD to calculate the candidate key.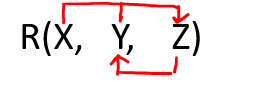

From the above arrow diagram on R, we can see that an attribute X is not determined by any of the given FD, hence X will be the integral part of the Candidate key, i.e. no matter what will be the candidate key, and how many will be the candidate key, but all will have X compulsory attribute.

Let us calculate the closure of X

X + = X(from the closure method we studied earlier)

Since the closure of X contains only X, hence it is not a candidate key.

Let us check the combination of Y, i.e. XY, XZ.

a) XY + = XYZ ( from the closure method we studied earlier)

Since the closure of XY contains all the attributes of R, hence XY is Candidate Key

b) XZ + = XZY (from the closure method we studied earlier)

Since the closure of XZ contains all the attributes of R, hence XZ is Candidate Key

Hence there are two candidate key XY and XZ

Since R has 3 attributes: - X, Y, Z, and Candidate Key is XY and XZ, Therefore, prime attribute(part of candidate key) are X, Y, and Z while a non-prime attribute is none.

Using the Definition of 3NF to check whether R is in 3NF?: First, it should be in 2NF and if there exists a non-trivial dependency between two sets of attributes X and Y such that X → Y ( i.e. Y is not a subset of X) then

a) Either X is Super Key

b) Or Y is a prime attribute.

Given FD are XY → Z, and Z → Y and Super Key / Candidate Key are XZ and XY

a) FD: X Y → Z satisfies the definition of 3NF, as XY is Super Key also Z is a prime attribute.

b) FD: Z → Y satisfies the definition of 3NF, even though Z is not Super Key but Y is a prime attribute.

Since both FD of R, XY → Z and Z → Y satisfy the definition of 3NF hence R is in 3 NF

Using the Definition of BCNF to check whether R is in BCNF?: First, it should be in 3NF and if there exists a non-trivial dependency between two sets of attributes X and Y such that X → Y ( i.e. Y is not a subset of X) then

a) X is Super Key

Given FD are XY → Z, and Z → Y and Super Key / Candidate Key is XZ and XY

b) FD: X Y → Z satisfies the definition of BCNF, as XY is Super Key.

c) FD: Z → Y does not satisfy the definition of BCNF, as Z is not Super Key Since both FD of R, XY → Z and Z → Y satisfy the definition of 3NF hence R is in 3 NF

Convert the table R( X, Y, Z) into BCNF:

Since due to FD: Z → Y, our table was not in BCNF, let's decompose the table

FD: Z→ Y was creating an issue, hence one table R1( Z, Y )

Create Table for key XY R2(X, Y) as XY was candidate key

Create Table for key XZ R2(X, Z) as XZ was candidate key

Note: When we have more than one key( eg: XY and XY) then while decomposing keep in mind that you compare both R2 and R3 with R1 such that among R1 and R2 or R1 and R3 there should be at least one common attribute and, that common attribute must be key in any of the table.

Considering R1( Z, Y) and R2(X, Y) both tables have one common attribute Y, but Y is not key in any of the table R1 and R2, hence we discard R2(X, Y) i.e. discarding candidate key XY.

Considering R1( Z, Y) and R3(X, Z) both tables have one common attribute Z, and Z is key of the table R1, hence we include R3(X, Z) i.e. including candidate key XZ.

Hence decomposed tables which are in BCNF:

R1(Z, Y)

R2(X, Z)

Question 2: Given a relation R( X, Y, Z) and Functional Dependency set FD = { X → Y and Y → Z }, determine whether the given R is in BCNF? If not convert it into BCNF.

Solution: Let us construct an arrow diagram on R using FD to calculate the candidate key.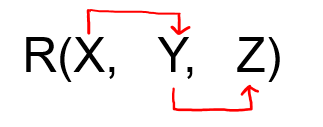

From the above arrow diagram on R, we can see that an attribute X is not determined by any of the given FD, hence X will be the integral part of the Candidate key, i.e. no matter what will be the candidate key, and how many will be the candidate key, but all will have X compulsory attribute.

Let us calculate the closure of X

X + = XYZ (from the closure method we studied earlier)

Since the closure of X contains all the attributes of R, hence X is Candidate Key

From the definition of Candidate Key (Candidate Key is a Super Key whose no proper subset is a Super key)

Using the Definition of BCNF to check whether R is in BCNF?: First, it should be in 3NF and if there exists a non-trivial dependency between two sets of attributes X and Y such that X → Y ( i.e. Y is not a subset of X) then

a) X is Super Key

First, we check that table is in 3NF?

Using the Definition of 3NF to check whether R is in 3NF?: If there exists a non-trivial dependency between two sets of attributes X and Y such that X → Y ( i.e. Y is not a subset of X) then

a) Either X is Super Key

b) Or Y is a prime attribute.

a) FD: X → Y is in 3NF (as X is a super Key)

b) FD: Y → Z is not in 3NF (as neither Y is Key nor Z is a prime attribute)

Hence because of Y → Z using definition 2 of 3NF, we can say that above table R is not in 3NF.

Convert the table R( X, Y, Z) into 3NF:

Since due to FD: Y → Z our table was not in 3NF, let's decompose the table

FD: Y → Z was creating issue, hence one table R1(Y, Z)

Create one Table for key X, R2(X, Y), since X → Y

Hence decomposed tables which are in 3NF:

R1(X, Y)

R2(Y, Z)

Both R1(X, Y) and R2(Y, Z) are in BCNF

Conclusion: From the above three examples we can conclude that the following steps are followed to check whether the given relational schema R is in 3 NF or not? If not, how to decompose it into 3 NF.

STEP 1: Calculate the Candidate Key of given R by using an arrow diagram and then using the closure of an attribute on R, such that from the calculated candidate key, we can separate the prime attributes and non-prime attributes.

STEP 2: Verify each FD with Definition of BCNF (First it should be in 3NF and if there exist a non-trivial dependency between two sets of attributes X and Y such that X → Y (i.e., Y is not a subset of X) then X is Super Key

STEP 3: Make a set of FD which does not satisfy BCNF, i.e. all those FD which do not have an attribute on the left side of FD as a super key

STEP 4: Convert the table R in BCNF by decomposing R such that each decomposition based on FD should satisfy the definition of BCNF.

STEP 5: Once the decomposition based on FD is completed, create a separate table of attributes in the Candidate key.

STEP 6: All the decomposed R obtained from STEP 4 and STEP 5 forms the required decomposition where each decomposition is in BCNF.