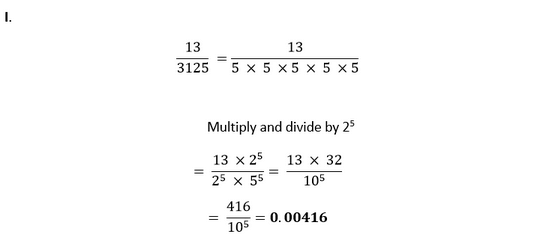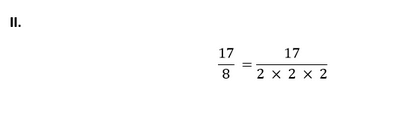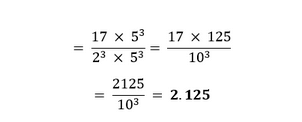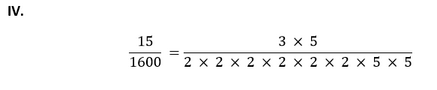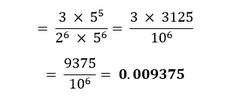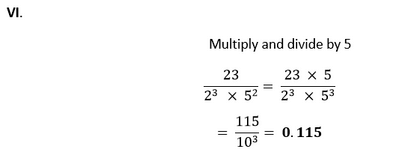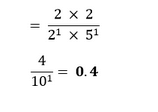NCERT Solutions Class 10 Maths Chapter 1 : Real NumbersExercise 1.11. Use Euclid's division algorithm to find the HCF of:
Solution I. Since 225 > 135, we can apply Euclid's Division Algorithm a=bq + r; 0≤ r < b with a=225 and b=135. 225 = 135 × 1 + 90 where r=90 Since r≠0, we will re-apply the algorithm on b = 135, and r = 90 135 = 90×1 + 45 where r1=45 Since r1≠0, we will re-apply the algorithm on b1=90 and r1=45 90 = 45×2 + 0 where r2=0 We have r2=0 Therefore, the HCF of 135 and 225 is 45. II. Since 38220 > 196, we can apply Euclid's Division Algorithm a=bq + r; 0≤ r < b with a=38220 and b=196. 38220 = 196×195 + 0 We have r=0 Therefore, the HCF of 196 and 38220 is 196. III. Since 867 > 255, we can apply Euclid's Division Algorithm a=bq + r; 0≤ r < b with a=867 and b=255. 867 = 255 × 3 + 102 where r=102 Since r≠0, we will re-apply the algorithm on b = 255, and r = 102 255 = 102×2 + 51 where r1=51 Since r1≠0, we will re-apply the algorithm on b1=102 and r1=51 102 = 51×2 + 0 where r2=0 We have r2=0 Therefore, the HCF of 867 and 255 is 51. 2. Show that any positive odd integer is of the form 6q + 1, or 6q + 3, or 6q + 5, where q is some integer. Solution Let there be an odd positive integer a, such that a=6q + r; 0≤ r< 6 (By Euclid's Division Lemma) where q is the quotient and r is the remainder. Since 0≤ r< 6, we can put 0, 1, 2, 3, 4, or 5 in place of r. For each of the cases we get the following:
As given previously, a is an odd positive integer. Hence, r cannot be equal to 2 or 4 because a=6q, a=6q+2 and a=6q+4 present a as an even positive integer which is false. Hence, an odd positive integer can be only of the forms 6q+1, 6q+3 or 6q+5. 3. An army contingent of 616 members is to march behind an army band of 32 members in a parade. The two groups are to march in the same number of columns. What is the maximum number of columns in which they can march? Solution It is clear from the problem that we need to find the maximum number of columns, which is the HCF of 616 and 32. Since 616 > 32, we can apply Euclid's Division Algorithm a=bq + r; 0≤ r < b with a=867 and b=32. 616 = 32 × 19 + 8 where r=8 Since r≠0, we will re-apply the algorithm on b = 32, and r = 8 32 = 8×4 + 0 where r1=0 We have r1=0 Therefore, the HCF of 616 and 32 is 8. Hence, the maximum number of columns the army contingent of 616 members can march behind band of 32 members is 8. 4. Use Euclid's division lemma to show that the square of any positive integer is either of the form 3m or 3m + 1 for some integer m. Solution Let there be a positive integer a. After applying Euclid's division lemma with b=3 we get a=3q + r; 0≤ r< 3 Therefore, a can be of the forms a=3q, a=3q+1 or a=3q+2 Squaring both sides in each equation we get a2=9q2 a2=3(3q2) a2=3m; where m=3q2 a2=9q2+1+6q a2=3(3q2 +2q) +1 a2=3m+1; where m=3q2 +2q a2=9q2 +4+12q a2=3(3q2+4q+1) +1 a2=3m+1; where m=3q2+4q+1 Hence, square of any positive integer is always of the form 3m or 3m+1. 5. Use Euclid's division lemma to show that the cube of any positive integer is of the form 9m, 9m + 1 or 9m + 8. Solution Let a be positive integer. After applying Euclid's Division Lemma with b=3 we get a=3q+r; 0≤ r< 3 Therefore, a can be of the forms a=3q, a=3q+1 or a=3q+2 Cubing both sides of each equation we get a3=27q3 a3=9(3q3) a3=9m where m=3q3 a3=27q3 + 1+ 27q3+ 9q a3=9(3q3+3q2 + q) +1 a3=9m+1 where m=3q3+3q2 + q a3=27q3+ 8+ 54q3+36q a3=9(3q3+6q2 + 4q) +8 a3=9m +8 where m=3q3+6q2 + 4q Hence, cube of any positive integer is always of the form 9m, 9m+1, or 9m+8. Exercise 1.21. Express each number as a product of its prime factors:
I. By applying prime factorization, 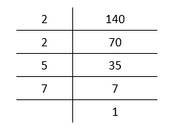
II. By applying prime factorization, 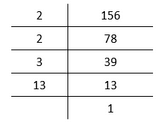
III. By applying prime factorization, 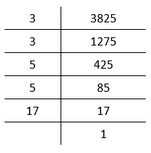
IV. By applying prime factorization, 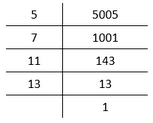
V. By applying prime factorization, 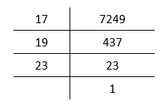
2. Find the LCM and HCF of the following pairs of integers and verify that LCM × HCF = product of the two numbers.
Solution I. Apply prime factorization to find LCM and HCF 26 = 2 × 13 And 91 = 7 × 13 Therefore, HCF(26, 91)=13 and LCM(26, 91) = 2 × 7 × 13 = 182. Product of both numbers = 26 × 91 = 2366 LCM × HCF = 182 × 13= 2366. Hence, product of the two numbers has been verified to be equal to LCM × HCF. II. Apply prime factorization to find LCM and HCF 510 = 2 × 3 × 5 × 17 And 92 = 2 × 2 × 23 Therefore, HCF(510, 92) = 2 and LCM(510, 92) = 2 × 2 × 3 × 5 × 17 × 23 = 23460. Product of both numbers = 510 × 92 = 46920 LCM × HCF = 23460 × 2 = 46920. Hence, product of the two numbers has been verified to be equal to LCM × HCF. III. Apply prime factorization to find LCM and HCF 336 = 2 × 2 × 2 × 2 × 3 × 7 And 54 = 2 × 3 × 3 × 3 Therefore, HCF(336, 54) = 2 × 3 = 6 and LCM(336, 54) = 2 × 2 × 2 × 2 × 3 × 3 × 3 × 7 = 3024. Product of both numbers = 336 × 54 = 18144 LCM × HCF = 3024 × 6 = 18144. Hence, product of the two numbers has been verified to be equal to LCM × HCF. 3. Find the LCM and HCF of the following integers by applying the prime factorization method.
Solution I. By performing prime factorization, we get 12 = 2 × 2 × 3 15 = 3 × 5 21 = 3 × 7 HCF (12, 15, 21) = 3 LCM (12, 15, 21) = 2 × 2 × 3 × 5 × 7 = 420 II. By performing prime factorization, we get 17 = 17 × 1 23 = 23 × 1 29 = 29 × 1 HCF (17, 23, 29) = 1 LCM (17, 23, 29) = 17 × 23 × 29 = 11339 III. By performing prime factorization, we get 8 = 2 × 2 × 2 9 = 3 × 3 × 3 25 = 5 × 5 HCF (8, 9, 25) = 1 LCM (8, 9, 25) = 2 × 2 × 2 × 3 × 3 × 5 × 5 = 1800 4. Given that HCF (306, 657) = 9, find LCM (306, 657). Solution Since, it is known that Product of two given numbers = LCM × HCF Therefore, 306 × 657 = LCM × 9 Solving the above equation, we get LCM = 22338 Hence, LCM (306, 657) = 22338 5. Check whether 6n can end with the digit 0 for any natural number n. Solution 6n will end with a 0 if and only if 5 is one of the prime factors of 6. By using prime factorization, we have 6 = 2 × 3 Since, 5 is not a prime factor of 6, 6n can never end with the digit 0. 6. Explain why 7 × 11 × 13 + 13 and 7 × 6 × 5 × 4 × 3 × 2 × 1 + 5 are composite numbers. Solution Let 7 × 11 × 13 + 13 = a and 7 × 6 × 5 × 4 × 3 × 2 × 1 + 5 = b. a = 7 × 11 × 13 + 13 = 13 × (7 × 11 × 1 + 1) = 13 × (77 + 1) = 13 × 78 = 13 × 2 × 3 × 13 (Prime Factorization of 78) Since a can be expressed as a product of primes, it is a composite number. b = 7 × 6 × 5 × 4 × 3 × 2 + 5 = 5 × (7 × 6 × 1 × 4 × 3 × 2 + 1) =5 × (1008 + 1) = 5 × 1009 Since b can be expressed as a product of primes, it is a composite number. Hence, 7 × 11 × 13 + 13 and 7 × 6 × 5 × 4 × 3 × 2 × 1 + 5 are both composite numbers. 7. There is a circular path around a sports field. Sonia takes 18 minutes to drive one round of the field, while Ravi takes 12 minutes for the same. Suppose they both start at the same point and at the same time, and go in the same direction. After how many minutes will they meet again at the starting point? Solution Sonia takes 18 minutes while Ravi takes 12 minutes. In order to find the time elapsed (in minutes) when they meet again at the starting point, we need to calculate the LCM of 18 and 12 (time taken by each of them to complete a round). By Prime factorization, 18 = 2 × 3 × 3 12 = 2 × 2 × 3 LCM = 2 × 2 × 3 × 3 = 36 Hence, it will take them 36 minutes to meet again at the starting point. Exercise 1.31. Prove that √5 is irrational. Solution Let us assume that √5 is a rational. Since, √5 is rational, there exists two coprime integers a and b; b ≠ 0 such that √5= a/b b√5= a Squaring both sides 5b2 = a2 … (I) From the equation, it can be deduced that a2 is divisible by 5, which further implies that a is also divisible by 5. Therefore, we can write a = 5c where c is an integer. If we substitute this value of a in (I), we get 5b2 = 25c2 b2 = 5c2 From the equation, it can be deduced that b2 is divisible by 5, which further implies that b is also divisible by 5. Hence, a and b are both divisible by 5. This contradicts the fact that a and b are coprime integers as they both have 5 as a common factor. The contradiction has arisen due to our wrong assumption that √5 is rational. Hence, √5 is irrational. 2. Prove that 3 + 2√5 is irrational. Solution Let us assume that 3 + 2√5 is rational. Since, 3 + 2√5 is rational, there exists two coprime integers a and b; b ≠ 0 such that 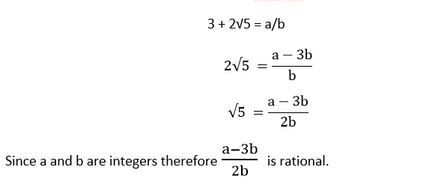
But √5 is irrational because of the following proof: (NOTE: It is not necessary for students to add the following proof when answering the questions unless the question awards more than 3 marks)Let us assume that √5 is a rational. Since, √5 is rational, there exists two coprime integers a and b; b ≠ 0 such that √5= a/b b√5= a Squaring both sides 5b2 = a2 … (I) From the equation, it can be deduced that a2 is divisible by 5, which further implies that a is also divisible by 5. Therefore, we can write a = 5c where c is an integer. If we substitute this value of a in (I), we get 5b2 = 25c2 b2 = 5c2 From the equation, it can be deduced that b2 is divisible by 5, which further implies that b is also divisible by 5. Hence, a and b are both divisible by 5. This contradicts the fact that a and b are coprime integers as they both have 5 as a common factor. The contradiction has arisen due to our wrong assumption that √5 is rational. Hence, √5 is irrational. From the above proof it is clear that √5 is irrational. This contradicts the assumption that 3 + 2√5 is rational. Hence, 3 + 2√5 is irrational. 3. Prove that the following are irrationals:
Solution I. Let us assume that √2 is rational. Since, √2 is rational, there exist two coprimes a and b; b ≠ 0 such that √2 = a/b. √2b = a Squaring both sides, we get 2b2 = a2 …(I) We can deduce that a2 is divisible by 2, hence a is also divisible by 2. Therefore, a = 2c for some integer c. Substituting value of a in (I) we get 2b2 = 4c2 b2 = 2c2 This implies that b2 is divisible by 2, hence b is also divisible by 2. Therefore, a and b have 2 as a common factor. This contradicts the fact that a and b are coprimes. The contradiction has arisen due to our wrong assumption that √2 is rational. Hence, √2 is irrational. This implies that 1/√2 is also irrational. II. Let us assume that √5 is a rational. Since, √5 is rational, there exists two coprime integers a and b; b ≠ 0 such that √5= a/b b√5= a Squaring both sides 5b2 = a2 … (I) From the equation, it can be deduced that a2 is divisible by 5, which further implies that a is also divisible by 5. Therefore, we can write a = 5c where c is an integer. If we substitute this value of a in (I), we get 5b2 = 25c2 b2 = 5c2 From the equation, it can be deduced that b2 is divisible by 5, which further implies that b is also divisible by 5. Hence, a and b are both divisible by 5. This contradicts the fact that a and b are coprime integers as they both have 5 as a common factor. The contradiction has arisen due to our wrong assumption that √5 is rational. Hence, √5 is irrational. This implies that 7√5 is also irrational. III. Let us assume that 6 + √2 is a rational. Since, 6 + √2 is rational, there exists two coprime integers a and b; b ≠ 0 such that 6 + √2 = a/b. 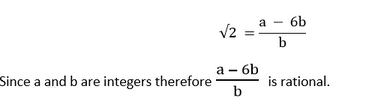
Therefore, √2 is also rational. But √2 is irrational because of the following proof: (NOTE: It is not necessary for students to add the following proof when answering the questions unless the question awards more than 3 marks)Let us assume that √2 is a rational. Since, √2 is rational, there exists two coprime integers a and b; b ≠ 0 such that √2= a/b b√2= a Squaring both sides 2b2 = a2 … (I) From the equation, it can be deduced that a2 is divisible by 2, which further implies that a is also divisible by 2. Therefore, we can write a = 2c where c is an integer. If we substitute this value of a in (I), we get 2b2 = 4c2 b2 = 2c2 From the equation, it can be deduced that b2 is divisible by 2, which further implies that b is also divisible by 2. Hence, a and b are both divisible by 2. This contradicts the fact that a and b are coprime integers as they both have 2 as a common factor. The contradiction has arisen due to our wrong assumption that √2 is rational. Hence, √2 is irrational. From the above proof it is clear that √2 is irrational. This contradicts the assumption that 6 + √2 is rational. Hence, 6 + √2 is irrational. Exercise 1.41. Without actually performing the long division, state whether the following rational numbers will have a terminating decimal expansion or a non-terminating repeating decimal expansion:
Solution 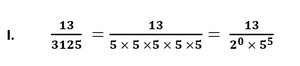
Since, the given number can be represented in the form of p/q where p and q are coprimes and q is of the form 2n5m. Therefore, the given number has a terminating decimal expansion. 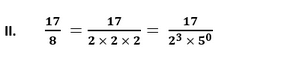
Since, the given number can be represented in the form of p/q where p and q are coprimes and q is of the form 2n5m. Therefore, the given number has a terminating decimal expansion. 
Since, the given number cannot be represented in the form of p/q where p and q are coprimes and q is of the form 2n5m. Therefore, the given number has a non-terminating repeating decimal expansion. 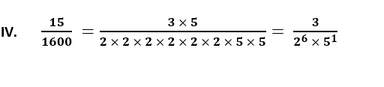
Since, the given number can be represented in the form of p/q where p and q are coprimes and q is of the form 2n5m. Therefore, the given number has a terminating decimal expansion. 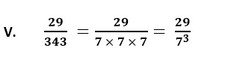
Since, the given number cannot be represented in the form of p/q where p and q are coprimes and q is of the form 2n5m. Therefore, the given number has a non-terminating repeating decimal expansion. 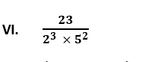
Since, the given number can be represented in the form of p/q where p and q are coprimes and q is of the form 2n5m. Therefore, the given number has a terminating decimal expansion. 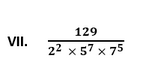
Since, the given number cannot be represented in the form of p/q where p and q are coprimes and q is of the form 2n5m. Therefore, the given number has a non-terminating repeating decimal expansion. 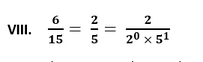
Since, the given number can be represented in the form of p/q where p and q are coprimes and q is of the form 2n5m. Therefore, the given number has a terminating decimal expansion. 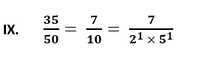
Since, the given number can be represented in the form of p/q where p and q are coprimes and q is of the form 2n5m. Therefore, the given number has a terminating decimal expansion. 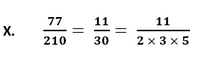
Since, the given number cannot be represented in the form of p/q where p and q are coprimes and q is of the form 2n5m. Therefore, the given number has a non-terminating repeating decimal expansion. 2. Write down the decimal expansions of those rational numbers in Question 1 above which have terminating decimal expansions. Solution I, II, IV, VI, VIII, IX in question 1 have a terminating decimal expansion. These can be calculated as follows:
Multiply and divide by 53
Multiply and divide by 54
Multiply and divide by 2
3. The following real numbers have decimal expansions as given below. In each case, decide whether they are rational or not. If they are rational, and of the form p/q what can you say about the prime factors of q?
Solution I. Since, the given decimal expansion is terminating, it is a rational. 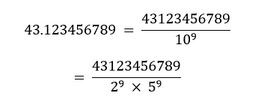
The denominator q can be expressed in the form of 2n5m. II. Since, the given decimal expansion is non-terminating non-repeating, it is irrational and hence the denominator cannot be represented as 2n5m. III. Since, the given decimal expansion is non-terminating repeating, it is rational but the denominator cannot be expressed in the form of 2n5m.
Next TopicClass 10 Maths Chapter 2
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share