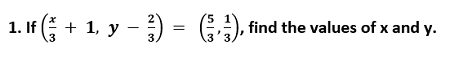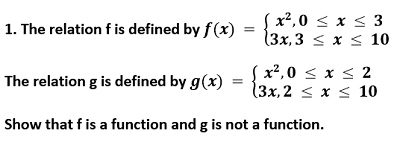NCERT Solutions Class 11^th Maths Chapter 2: Relations and Functions

Exercise 2.1

SOLUTION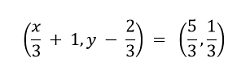

Since, the ordered pairs are equal. Therefore, the corresponding elements on both sides must be equal as well.

x/3 + 1 = 5/3

x/3 = 2/3

x = 2

y - 2/3 = 1/3

y = 1

Hence, x = 2 and y = 1.

2. If the set A has 3 elements and the set B = {3, 4, 5}, then find the number of elements in (A × B).

SOLUTION

Number of elements in set A = 3

Number of elements in set B = 3

Number of elements in (A × B) = 3 × 3 = 9

Hence, A × B has 9 elements.

3. If G = {7, 8} and H = {5, 4, 2}, find G × H and H × G.

SOLUTION

We know that for any two sets P and Q, the Cartesian product is defined as:

P × Q = {(p, q): where p ∈ P, q ∈ Q}

Therefore,

G × H = {(7, 5), (7, 4), (7, 2), (8, 5), (8, 4), (8, 2)}

H × G = {(5, 7), (5, 8), (4, 7), (4, 8), (2, 7), (2, 8)}

4. State whether each of the following statements are true or false. If the statement is false, rewrite the given statement correctly.

1. If P = {m, n} and Q = { n, m}, then P × Q = {(m, n),(n, m)}.
2. If A and B are non-empty sets, then A × B is a non-empty set of ordered pairs (x, y) such that x ∈ A and y ∈ B.
3. If A = {1, 2}, B = {3, 4}, then A × (B ∩ φ) = φ.

SOLUTION

(i) This statement is false.

Correct statement is

If P = {m, n} and Q = {n, m}, then P × Q = {(m, n), (m, m), (n, n), (n, m)}.

(ii) This statement is true as for any two sets P and Q, the Cartesian product is defined as:

P × Q = {(p, q): where p ∈ P, q ∈ Q}

(iii) This statement is true as B ∩ φ is φ.

5. If A = {-1, 1}, find A × A × A.

SOLUTION

A × A × A = {(a, b, c):a, b, c∈A}

A × A × A = {(-1, -1, -1), (-1, -1, 1), (-1, 1, -1), (-1, 1, 1), (1, -1, -1), (1, -1, 1), (1, 1, -1), (1, 1, 1)}

6. If A × B = {(a, x),(a , y), (b, x), (b, y)}. Find A and B.

SOLUTION

We know that for any two sets P and Q, the Cartesian product is defined as:

P × Q = {(p, q): where p ∈ P, q ∈ Q}. Therefore,

A is the set of all the first elements and B is the set of all the second elements.

Hence, A = {a, b} and B = {x, y}.

7. Let A = {1, 2}, B = {1, 2, 3, 4}, C = {5, 6} and D = {5, 6, 7, 8}. Verify that

(i) A × (B ∩ C) = (A × B) ∩ (A × C). (ii) A × C is a subset of B × D.

SOLUTION

(i) LHS = A × (B∩C) = A ×φ =φ

RHS = (A × B) ∩ (A × C)

= {(1, 1), (1, 2), (1, 3), (1, 4), (2, 1), (2, 2), (2, 3), (2, 4)} ∩ {(1, 5), (1, 6), (2, 5), (2, 6)}

= φ

LHS = RHS. Hence, verified.

(ii) A × C = {(1, 5), (1, 6), (2, 5), (2, 6)}

B × D = {(1, 5), (1, 6), (1, 7), (1, 8), (2, 5), (2, 6), (2, 7), (2, 8), (3, 5), (3, 6), (3, 7), (3, 8), (4, 5), (4, 6), (4, 7), (4, 8)}

It can be observed that (A × C) ⊂ (B × D).

Hence, verified.

8. Let A = {1, 2} and B = {3, 4}. Write A × B. How many subsets will A × B have? List them.

SOLUTION

We know that for any two sets P and Q, the Cartesian product is defined as:

P × Q = {(p, q): where p ∈ P, q ∈ Q}

Therefore,

A × B = {(1, 3), (1, 4), (2, 3), (2, 4)}

n[P (A × B)] = 2^{n (A × B)}

= 2⁴ = 16

Therefore, A × B has 16 subsets.

P (A × B) = φ, {(1, 3)}, {(1, 4)}, {(2, 3)}, {(2, 4)}, {(1, 3), (1, 4)}, {(1, 3), (2, 3)}, {(1, 3), (2, 4)}, {(1, 4), (2, 3)}, {(1, 4), (2, 4)}, {(2, 3), (2, 4)}, {(1, 3), (1, 4), (2, 3)}, {(1, 3), (1, 4), (2, 4)}, {(1, 3), (2, 3), (2, 4)}, {(1, 4), (2, 3), (2, 4)}, {(1, 3), (1, 4), (2, 3), (2, 4)}

9. Let A and B be two sets such that n(A) = 3 and n(B) = 2. If (x, 1), (y, 2), (z, 1) are in A × B, find A and B, where x, y and z are distinct elements.

SOLUTION

We know that for any two sets P and Q, the Cartesian product is defined as:

P × Q = {(p, q): where p ∈ P, q ∈ Q}. Therefore,

A is the set of all the first elements and B is the set of all the second elements.

Hence, A = {x, y, z} and B = {1, 2} as

10. The Cartesian product A × A has 9 elements among which are found (-1, 0) and (0,1). Find the set A and the remaining elements of A × A.

SOLUTION

n (A × A) = n (A) × n (A)

9 = n (A) × n (A)

Therefore, n (A) = 3.

We know that for a set P, the Cartesian product is defined as:

P × P = {(p, p): where p ∈ P}.

Since, two of the elements in A × A are (-1, 0) and (0, 1). Therefore, we can conclude that A = {-1, 0, 1}.

Hence, all the remaining elements of A × A are:

(-1, -1), (-1, 1), (0, -1), (0, 0), (1, -1), (1, 0), and (1, 1)

Exercise 2.2

1. Let A = {1, 2, 3,...,14}. Define a relation R from A to A by R = {(x, y) : 3x - y = 0, where x, y ∈ A}. Write down its domain, codomain and range.

SOLUTION

3x - y = 0

3x = y

Therefore, R = {(1, 3), (2, 6), (3, 9), (4, 12)}

All the first elements of the ordered pairs will form the domain of R.

Domain of R = {1, 2, 3, 4}

Codomain of R = A = {1, 2, 3, ..., 14}

All the second elements of the ordered pairs will form the domain of R.

Range of R = {3, 6, 9, 12}

2. Define a relation R on the set N of natural numbers by R = {(x, y) : y = x + 5, x is a natural number less than 4; x, y ∈N}. Depict this relationship using roster form. Write down the domain and the range.

SOLUTION

Natural numbers less than 4 are: 1, 2 and 3.

Therefore,

R = {(1, 6), (2, 7), (3, 8)}

All the first elements of the ordered pairs will form the domain of R.

Domain of R = {1, 2, 3}

All the second elements of the ordered pairs will form the domain of R.

Range of R = {6, 7, 8}

3. A = {1, 2, 3, 5} and B = {4, 6, 9}. Define a relation R from A to B by R = {(x, y): the difference between x and y is odd; x ∈ A, y ∈ B}. Write R in roster form.

SOLUTION

Difference between x and y must be odd. We know that the difference between two odd numbers and difference between two even numbers is always even. Therefore,

R = {(1, 4), (1, 6), (2, 9), (3, 4), (3, 6), (5, 4), (5, 6)}

4. The Fig2.7 shows a relationship between the sets P and Q. Write this relation

(i) in set-builder form (ii) roster form.

What is its domain and range?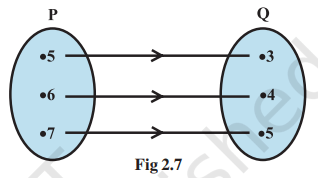

SOLUTION

P = {5, 6, 7} and Q = {3, 4, 5}

(i) R = {(x, y): x = y + 2 where x ∈ P and y ∈ Q}

(ii) R = {(5, 3), (6, 4), (7, 5)}

Domain of R = {5, 6, 7} (First elements of the ordered pairs)

Range of R = {3, 4, 5} (Second elements of the ordered pairs)

5. Let A = {1, 2, 3, 4, 6}. Let R be the relation on A defined by {(a, b): a , b ∈A, b is exactly divisible by a}.

1. Write R in roster form
2. Find the domain of R
3. Find the range of R.

SOLUTION

1. R = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 6), (2, 2), (2, 4), (2, 6), (3, 3), (3, 6), (4, 4), (6, 6)}
2. Domain of R = {1, 2, 3, 4, 6} (First elements of the ordered pairs)
3. Range of R = {1, 2, 3, 4, 6} (Second elements of the ordered pairs)

6. Determine the domain and range of the relation R defined by R = {(x, x + 5) : x ∈ {0, 1, 2, 3, 4, 5}}.

SOLUTION

R = {(0, 5), (1, 6), (2, 7), (3, 8), (4, 9), (5, 10)}

Domain of R = {0, 1, 2, 3, 4, 5} (First elements of the ordered pairs)

Range of R = {5, 6, 7, 8, 9, 10} (Second elements of the ordered pairs)

7. Write the relation R = {(x, x³ ) : x is a prime number less than 10} in roster form.

SOLUTION

Prime numbers less than 10 are: 2, 3, 5, and 7.

Therefore, R = {(2, 8), (3, 27), (5, 125), (7, 343)}

8. Let A = {x, y, z} and B = {1, 2}. Find the number of relations from A to B.\

SOLUTION

Cartesian product of A and B = A × B

= {(x, 1), (x, 2), (y, 1), (y, 2), (z, 1), (z, 2)}

n (A × B) = 6

Therefore, number of subsets of A × B = 2^{n (A × B)}

= 2⁶ = 64

9. Let R be the relation on Z defined by R = {(a,b): a, b ∈ Z, a - b is an integer}. Find the domain and range of R.

SOLUTION

In order for a - b to be an integer, a also needs to be an integers. Therefore,

Domain of R = Z

and Range of R = Z

Exercise 2.3

1. Which of the following relations are functions? Give reasons. If it is a function, determine its domain and range.

1. {(2,1), (5,1), (8,1), (11,1), (14,1), (17,1)}
2. {(2,1), (4,2), (6,3), (8,4), (10,5), (12,6), (14,7)}
3. {(1,3), (1,5), (2,5)}.

SOLUTION

1. Since, each element of the domain of the given relation has a unique image. Therefore, this relation is a function.
2. Since, each element of the domain of the given relation has a unique image. Therefore, this relation is a function.
3. Since, the element 1 of the domain of the given relation corresponds to more than one image. Therefore, this relation is not a function.

2. Find the domain and range of the following real functions:

(i) f(x) = - |x| (ii) f(x) = √(9 - x²)

SOLUTION

(i)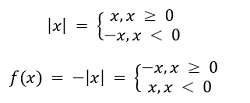

It is given that f(x) is defined for x ∈ R. Thus, R is the domain of the given function.

Since, the range of f(x) is negative real numbers and 0. Therefore, range of R is (-∞, 0].

(ii) Since, f(x) is real. Therefore,

9 - x² ≥ 0

9 ≥ x²

-3 ≤ x ≤ 3

Hence, domain of f(x) is {x: -3 ≤ x ≤ 3} OR [-3, 3]

and range of f(x) is {x: 0 ≤ x ≤ 3} or [0, 3] as for -3 ≤ x ≤ 3, the value of f(x) will be between 0 and 3.

3. A function f is defined by f(x) = 2x -5. Write down the values of

(i) f (0), (ii) f (7), (iii) f (-3).

SOLUTION

(i) f(x) = 2x - 5

f(0) = 2(0) - 5 = -5

(ii) f(x) = 2x - 5

f(7) = 2(7) - 5 = 9

(iii) f(x) = 2x - 5

f(-3) = 2(-3) - 5 = -11

4. The function 't' which maps temperature in degree Celsius into temperature in degree Fahrenheit is defined by t(C) = 9C/5 + 32.

Find

(i) t(0) (ii) t(28) (iii) t(-10)

(iv) The value of C, when t(C) = 212

SOLUTION

t(C) = 9C/5 + 32

(i) t(0) = 9(0)/5 + 32 = 32

(ii) t(28) = 9(28)/5 + 32

= 412/5

(iii) t(-10) = 9(-10)/5 + 32

= 14

(iv) t(C) = 212

9C/5 + 32 = 212

9C/5 = 180

9C = 900

C = 100

5. Find the range of each of the following functions.

1. f (x) = 2 - 3x, x ∈ R, x > 0.
2. f (x) = x2 + 2, x is a real number.
3. f (x) = x, x is a real number.

SOLUTION

(i) f(x) = 2 - 3x, x ∈ R and x > 0

x > 0

Multiply both sides by 3

3x > 0

Multiple both sides by -1

-3x < 0

Add 2 to both sides

2 - 3x < 2

f(x) < 2

Hence, the range of the given function is (-∞, 2)

Miscellaneous Exercise

SOLUTION

f(x) = x² when 0 ≤ x ≤ 3

f(x) = 3x when 3 ≤ x ≤ 10

For x = 3:

f(x) = x² = 3² = 9

OR

f(x) = 3x = 3 × 3 = 9

x = 3 has one image which is '9'.

Since, the images of f(x) remain unique for 0 ≤ x ≤ 10. Therefore, the relation f is a function.

g(x) = x² when 0 ≤ x ≤ 2

g(x) = 3x when 2 ≤ x ≤ 10

For x = 2:

g(x) = x² = 2² = 4

OR

g(x) = 3x = 3 × 2 = 6

x = 2 has two different images which are 4 and 6.

Since, one element of the domain of the relation g corresponds to more than one image. Therefore, the relation g is not a function.

Hence, proved.

2. If f (x) = x², find (f(1.1) - f(1))/(1.1 - 1).

SOLUTION

f(x) = x²

f(1.1) = 1.21

f(1) = 1

(f(1.1) - f(1))/(1.1 - 1) = (1.21 - 1)/0.1

= 0.21/0.1

= 2.1

3. Find the domain of the function f (x) = (x² + 2x + 1)/(x² - 8x + 12).

SOLUTION

Denominator of f(x) = x² - 8x + 12

= x² - 6x - 2x + 12

= x(x - 6) - 2(x - 6)

= (x - 6)(x - 2)

Therefore, f(x) will be defined for any real number except 2 and 6 as that would make the denominator zero and f(x) would become undefined.

Hence, Domain of f = {2, 6}

4. Find the domain and the range of the real function f defined by f (x) = √(x - 1).

SOLUTION

Since function f is real. Therefore,

√(x - 1) ≥ 0

x - 1 ≥ 0

x ≥ 1

Hence,

Domain of f = [1, ∞)

Range of f = [0, ∞) (As √(x - 1) ≥ 0)

5. Find the domain and the range of the real function f defined by f (x) = |x -1| .

SOLUTION

It is given that f(x) = |x - 1| is a real function.

|x - 1| will be defined for all real numbers.

So, Domain of f = R

|x - 1| will always return a non-negative value.

Thus, Range of f is the set of all non-negative real numbers.

SOLUTION

It is clear that x² > 1 + x².

Therefore, x²/(1 + x²) can only be greater than or equal to 0 and smaller than 1.

Thus, 0 ≤ x²/(1 + x²) < 1.

Hence, the range of f will be [0, 1).

7. Let f, g : R→R be defined, respectively by f(x) = x + 1, g(x) = 2x - 3. Find f + g, f - g and f/g.

SOLUTION

It is given that the functions f, g:R→Ris defined as

f(x) = x + 1 and g(x) = 2x - 3

Thus,

(f + g)(x) = f(x) + g(x)

= (x + 1) + (2x - 3) = 3x - 2

Therefore, (f + g)(x) = 3x - 2

(f - g)(x) = f(x) - g(x)

= (x + 1) - (2x - 3) = x + 1 - 2x + 3

= 4 - x

Therefore, (f - g)(x) = 4 - x

f/g(x) = f(x)/g(x) where g(x) ≠ 0 and x is real

= (x + 1)/ (2x - 3) where 2x - 3 ≠ 0 and x is real

= (x + 1)/ (2x - 3) where 2x ≠ 3 and x is real

= (x + 1)/ (2x - 3) where x ≠ 3/2 and x is real

Therefore, f/g(x) = (x + 1)/ (2x - 3) where x ≠ 3/2 and x is real

8. Let f = {(1,1), (2,3), (0,-1), (-1, -3)} be a function from Z to Z defined by f(x) = ax + b, for some integers a, b. Determine a, b.

SOLUTION

It is given that:

f = {(1, 1), (2, 3), (0, -1), (-1, -3)}

and this function is defined by f(x) = ax + b

Now, since (1, 1) ∈ f. Thus,

f(1) = 1

a(1) + b = 1

a + b = 1

a = 1 - b

Also, since (2, 3) ∈ f. Thus,

f(2) = 3

a(2) + b = 3

2a + b = 3

Substitute a = 1 - b in the above equation

2(1 - b) + b = 3

2 - 2b + b = 3

2 - b = 3

-b = 1

b = -1

So, a = 1 - b = 1 - (-1) => a = 2

Hence, a = 2 and b = -1.

9. Let R be a relation from N to N defined by R = {(a, b) : a, b ∈N and a = b² }. Are the following true?

(i) (a,a) ∈ R, for all a ∈ N (ii) (a,b) ∈ R, implies (b,a) ∈ R

(iii) (a,b) ∈ R, (b,c) ∈ R implies (a,c) ∈ R.

SOLUTION

(i) The given statement is false.

a = a² is only true for a = 1 when a ∈ N.

For any natural number greater than 1, a ≠ a². For example, if a = 2:

LHS = 2

RHS = 2² = 4

LHS ≠ RHS

(ii) The given statement is false.

If a = b² then b = a² can only be true if a = 1 and b = 1 when a, b ∈ N.

For any natural number greater than 1, b ≠ a². For example, if a = 4 and b = 2:

a = b² as 4 = 2²

b = 2

a² = 4² = 16

b ≠ a²

(iii) The given statement is false.

a = b² and b = c² implies that a = c².

This statement is only true for a = 1, b = 1 and c = 1 when a, b, c ∈ N.

For any natural number greater than 1, a ≠ c². For example, if a = 16, b = 4 and c = 2:

a = b² as 16 = 4²

b = c² as 4 = 2²

But, a ≠ c² as 16 ≠ 2²

10. Let A ={1,2,3,4}, B = {1,5,9,11,15,16} and f = {(1,5), (2,9), (3,1), (4,5), (2,11)} Are the following true?

(i) f is a relation from A to B (ii) f is a function from A to B.

Justify your answer in each case.

SOLUTION

A = {1, 2, 3, 4}

B = {1, 5, 9, 11, 15, 16}

Cartesian Product of A and B = A × B

= {(1, 1), (1, 5), (1, 9), (1, 11), (1, 15), (1, 16), (2, 1), (2, 5), (2, 9), (2, 11), (2, 15), (2, 16), (3, 1), (3, 5), (3, 9), (3, 11), (3, 15), (3, 16), (4, 1), (4, 5), (4, 9), (4, 11), (4, 15), (4, 16)}

(i) f = {(1, 5), (2, 9), (3, 1), (4, 5), (2, 11)}

It can be observed that f is the subset of A × B.

We know that a relation of set A to set B provided that they are non-empty, is always a subset of their Cartesian product, i.e, A × B.

Hence, we can conclude that the given statement is true.

(ii) It can be observed that the same first element corresponds to more than one distinct image. Hence, we can conclude that the given statement is false.

11. Let f be the subset of Z × Z defined by f = {(ab, a + b) : a, b ∈ Z}. Is f a function from Z to Z? Justify your answer.

SOLUTION

It is given that f is defined by f = {(ab, a + b): a, b ∈ Z}

f is not a function from Z to Z. If we take four integers: 1, 2, -1, -2, then

(1 × 2, 1 + 2) ∈ f

(2, 3) ∈ f AND

(-1 × (-2), -1 - 2) ∈ f

(2, -3) ∈ f

The first element 2 corresponds to more than one distinct image. Hence, f is not a function.

12. Let A = {9,10,11,12,13} and let f : A→N be defined by f (n) = the highest prime factor of n. Find the range of f.

SOLUTION

It is given that A = {9, 10, 11, 12, 13} and f: A ? N is defined as f(n) = the highest prime factor of n.

For each element in A:

f(9) = 3

f(10) = 5

f(11) = 11

f(12) = 3

f(13) = 13

Hence, range of f is {3, 5, 11, 13}