NCERT Solutions Class 10 Maths Chapter 11: ConstructionsExercise 11.1In each of the following, give the justification of the construction also: 1. Draw a line segment of length 7.6 cm and divide it in the ratio 5 : 8. Measure the two parts. Solution Steps for the construction are as follows:
Justification: A5C is parallel to A13B by construction. Therefore, we can use basic proportionality theorem in triangle AA13B. AC/BC = AA5/A5A13 By construction, AA5 has 5 equal divisions of segment AA13 and A5A13 has 8 equal divisions. Thus, AA5/A5A13= 5/8 Therefore, AC/BC = 5/8. Hence, the construction is justified. 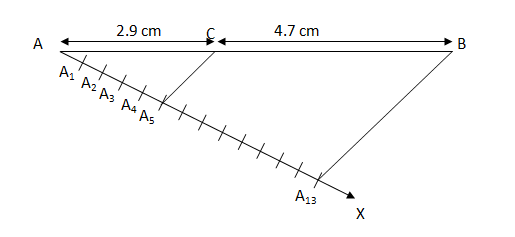
2. Construct a triangle of sides 4 cm, 5 cm and 6 cm and then a triangle similar to it whose sides are 2/3 of the corresponding sides of the first triangle. Solution Steps for the construction are as follows:
Justification: B'C' is parallel to BC by construction. Therefore ∠ABC = ∠AB'C' In ΔAB'C' and ΔABC, ∠ABC = ∠AB'C' (Already Proven) ∠BAC = ∠B'AC' (Common angle) Therefore, by the AA similarity criterion ΔAB'C' ∼ ΔABC. This implies that AB'/AB = B'C'/BC = AC'/AC (Corresponding sides of similar triangles) A2B' is parallel to A3B by construction. Therefore ∠AA2B' = ∠AA3B In ΔAA2B' and ΔAA3B, ∠A2AB' = ∠A3AB (Common angle) ∠AA2B' = ∠AA3B (Already Proven) Therefore, by the AA similarity criterion ΔAA2B' ~ ΔAA3B. This implies that AB'/AB = AA2/AA3 (Corresponding sides of similar triangles) By construction, AA2 has 2 equal divisions of segment AA3 and AA3 has 3 equal divisions. Thus, AA2/AA3 = 2/3 Therefore, AB'/AB = B'C'/BC = AC'/AC = 2/3 AB' = (2/3)AB B'C' = (2/3)BC AC'= (2/3)AC Hence, the construction is justified. 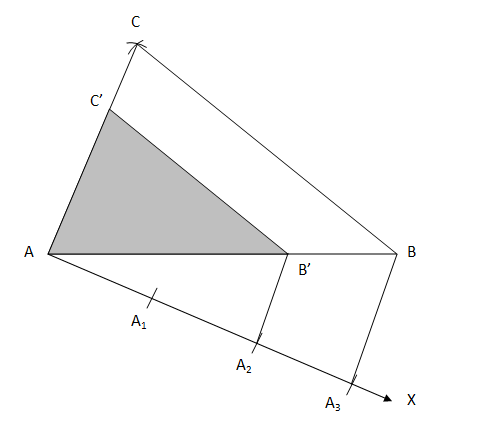
3. Construct a triangle with sides 5 cm, 6 cm and 7 cm and then another triangle whose sides are 7/5 of the corresponding sides of the first triangle. Solution Steps for the construction are as follows:
Justification: B'C' is parallel to BC by construction. Therefore ∠ABC = ∠AB'C' In ΔAB'C' and ΔABC, ∠ABC = ∠AB'C' (Already Proven) ∠BAC = ∠B'AC' (Common angle) Therefore, by the AA similarity criterion ΔAB'C' ∼ ΔABC. This implies that AB'/AB = B'C'/BC = AC'/AC (Corresponding sides of similar triangles) A7B' is parallel to A5B by construction. Therefore ∠AA7B' = ∠AA5B In ΔAA7B' and ΔAA5B, ∠A7AB' = ∠A5AB (Common angle) ∠AA7B' = ∠AA5B (Already Proven) Therefore, by the AA similarity criterion ΔAA7B' ~ ΔAA5B. This implies that AB'/AB = AA7/AA5 (Corresponding sides of similar triangles) By construction, AA7 has 7 equal divisions of segment AA7 and AA5 has 5 equal divisions. Thus, AA7/AA5 = 7/5 Therefore, AB'/AB = B'C'/BC = AC'/AC = 7/5 AB' = (7/5)AB B'C' = (7/5)BC AC'= (7/5)AC Hence, the construction is justified. 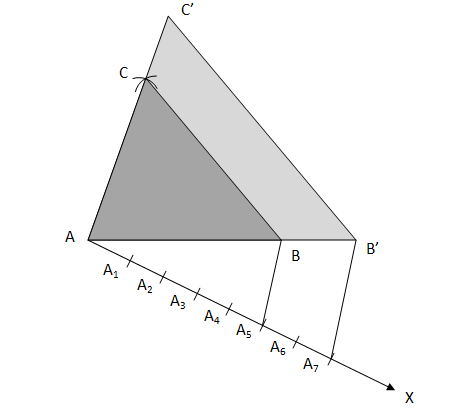
4. Construct an isosceles triangle whose base is 8 cm and altitude 4 cm and then another triangle whose sides are 1� times the corresponding sides of the isosceles triangle. Solution Steps for the construction are as follows:
Justification: A'C' is parallel to AC by construction. Therefore ∠A'C'B = ∠ACB In ΔA'BC' and ΔABC, ∠A'BC' = ∠ABC (Common angle) ∠A'C'B = ∠ACB (Already proven) Therefore, by the AA similarity criterion ΔA'BC' ∼ ΔABC. This implies that A'B/AB = BC'/BC= A'C'/AC (Corresponding sides of similar triangles) B2C is parallel to B3C' by construction. Therefore ∠BB2C = ∠BB3C' In ΔBB2C and ΔBB3C', ∠CBB2 = ∠C'BB3 (Common angle) ∠BB2C = ∠BB3C' (Already Proven) Therefore, by the AA similarity criterion ΔBB2C and ΔBB3C'. This implies that BB2/BB3 = BC/BC' (Corresponding sides of similar triangles) By construction, BB3 has 3 equal divisions of segment BB3 and BB2 has 2 equal divisions. Thus, BB2/BB3 = 2/3 Therefore, A'B/AB = BC'/BC = A'C'/AC = 3/2 A'B= (3/2)AB BC' = (3/2)BC A'C'= (3/2)AC Hence, the construction is justified. 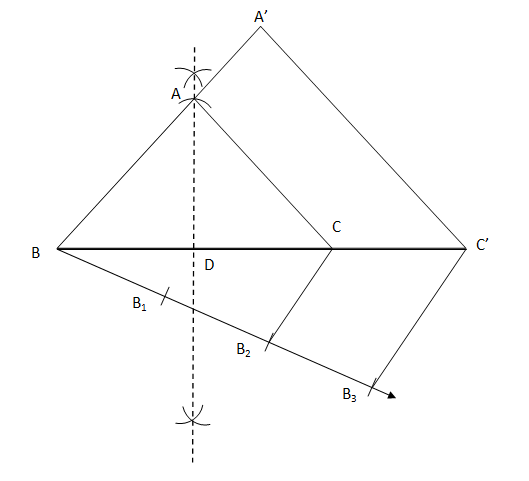
5. Draw a triangle ABC with side BC = 6 cm, AB = 5 cm and ∠ABC = 60°. Then construct a triangle whose sides are ¾ of the corresponding sides of the triangle ABC. Solution Steps for the construction are as follows:
Justification: A'C' is parallel to AC by construction. Therefore ∠A'C'B = ∠ACB In ΔA'BC' and ΔABC, ∠A'BC' = ∠ABC (Common angle) ∠A'C'B = ∠ACB (Already proven) Therefore, by the AA similarity criterion ΔA'BC' ∼ ΔABC. This implies that A'B/AB = BC'/BC= A'C'/AC (Corresponding sides of similar triangles) B4C is parallel to B3C' by construction. Therefore ∠BB4C = ∠BB3C' In ΔBB4C and ΔBB3C', ∠CBB4 = ∠C'BB3 (Common angle) ∠BB4C = ∠BB3C' (Already Proven) Therefore, by the AA similarity criterion ΔBB4C and ΔBB3C'. This implies that BB4/BB3 = BC/BC' (Corresponding sides of similar triangles) By construction, BB3 has 3 equal divisions of segment BB4 and BB4 has 4 equal divisions. Thus, BB4/BB3 = 4/3 Therefore, A'B/AB = BC'/BC = A'C'/AC = 3/4 A'B= (3/4)AB BC' = (3/4)BC A'C'= (3/4)AC Hence, the construction is justified. 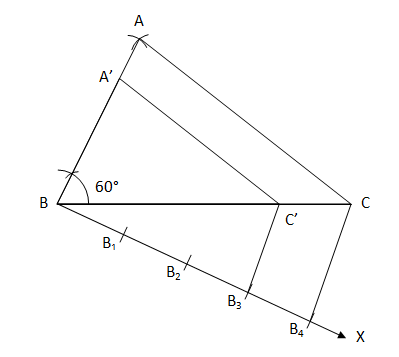
6. Draw a triangle ABC with side BC = 7 cm, ∠ B = 45°, ∠ A = 105°. Then, construct a triangle whose sides are 4/3 times the corresponding sides of ∆ ABC. Solution Steps for the construction are as follows:
Justification: A'C' is parallel to AC by construction. Therefore ∠A'C'B = ∠ACB In ΔA'BC' and ΔABC, ∠A'BC' = ∠ABC (Common angle) ∠A'C'B = ∠ACB (Already proven) Therefore, by the AA similarity criterion ΔA'BC' ∼ ΔABC. This implies that A'B/AB = BC'/BC= A'C'/AC (Corresponding sides of similar triangles) B3C is parallel to B4C' by construction. Therefore ∠BB3C = ∠BB4C' In ΔBB3C and ΔBB4C', ∠CBB3 = ∠C'BB4 (Common angle) ∠BB3C = ∠BB4C' (Already Proven) Therefore, by the AA similarity criterion ΔBB3C and ΔBB4C'. This implies that BB3/BB4 = BC/BC' (Corresponding sides of similar triangles) By construction, BB3 has 3 equal divisions of segment BB4 and BB4 has 4 equal divisions. Thus, BB3/BB4 = 3/4 Therefore, A'B/AB = BC'/BC = A'C'/AC = 4/3 A'B= (4/3)AB BC' = (4/3)BC A'C'= (4/3)AC Hence, the construction is justified. 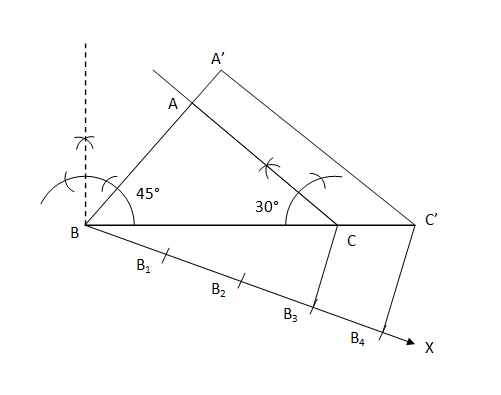
7. Draw a right triangle in which the sides (other than hypotenuse) are of lengths 4 cm and 3 cm. Then construct another triangle whose sides are 5/3 times the corresponding sides of the given triangle. Solution Steps for the construction are as follows:
Justification: A'C' is parallel to AC by construction. Therefore ∠A'C'B = ∠ACB In ΔA'BC' and ΔABC, ∠A'BC' = ∠ABC (Common angle) ∠A'C'B = ∠ACB (Already proven) Therefore, by the AA similarity criterion ΔA'BC' ∼ ΔABC. This implies that A'B/AB = BC'/BC= A'C'/AC (Corresponding sides of similar triangles) B3C is parallel to B5C' by construction. Therefore ∠BB3C = ∠BB5C' In ΔBB3C and ΔBB5C', ∠CBB3 = ∠C'BB5 (Common angle) ∠BB3C = ∠BB5C' (Already Proven) Therefore, by the AA similarity criterion ΔBB3C and ΔBB5C'. This implies that BB3/BB5 = BC/BC' (Corresponding sides of similar triangles) By construction, BB3 has 3 equal divisions of segment BB5 and BB5 has 5 equal divisions. Thus, BB3/BB5 = 3/5 Therefore, A'B/AB = BC'/BC = A'C'/AC = 5/3 A'B= (5/3)AB BC' = (5/3)BC A'C'= (5/3)AC Hence, the construction is justified. 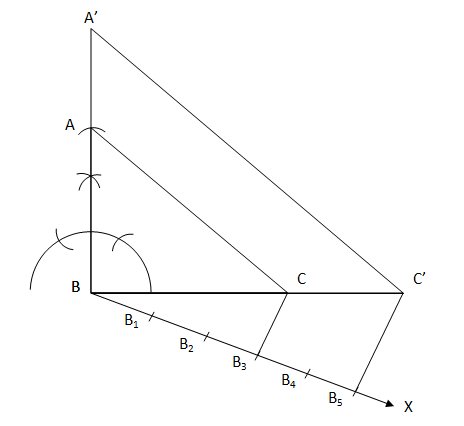
Exercise 11.2In each of the following, give also the justification of the construction: 1. Draw a circle of radius 6 cm. From a point 10 cm away from its centre, construct the pair of tangents to the circle and measure their lengths. Solution Steps for the construction are as follows:
Justification: We need to connect O with B and C. ∠B is an angle in a semi-circle subtended by a diameter. Therefore, it will be a right angle. This means that OB will be perpendicular to AB. Since, the radius OB of the circle is perpendicular to the line AB that touches it at one point. Therefore, AB is a tangent to this circle. Similarly, AC is a tangent to this circle. Hence, the construction is justified. 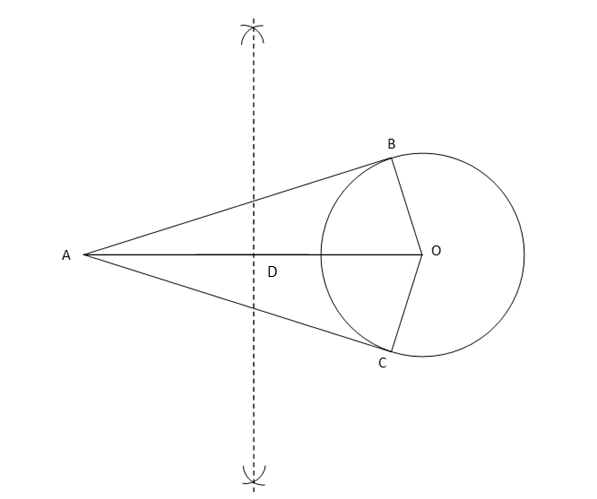
2. Construct a tangent to a circle of radius 4 cm from a point on the concentric circle of radius 6 cm and measure its length. Also verify the measurement by actual calculation. Solution Steps for the construction are as follows:
Verification: ABO forms a right triangle. Therefore, by using Pythagoras Theorem in ABO: AO2 = AB2 + OB2 62 = AB2 + 42 36 - 16 = AB2 20 = AB2 AB = √20 cm AB = 4.47 cm Tangents to a circle from an external point are equal, so AB = AC = 4.47 cm The result has been verified. Justification: We need to connect O with B and C. ∠B is an angle in a semi-circle subtended by a diameter. Therefore, it will be a right angle. This means that OB will be perpendicular to AB. Since, the radius OB of the circle is perpendicular to the line AB that touches it at one point. Therefore, AB is a tangent to this circle. Similarly, AC is a tangent to this circle. Hence, the construction is justified. 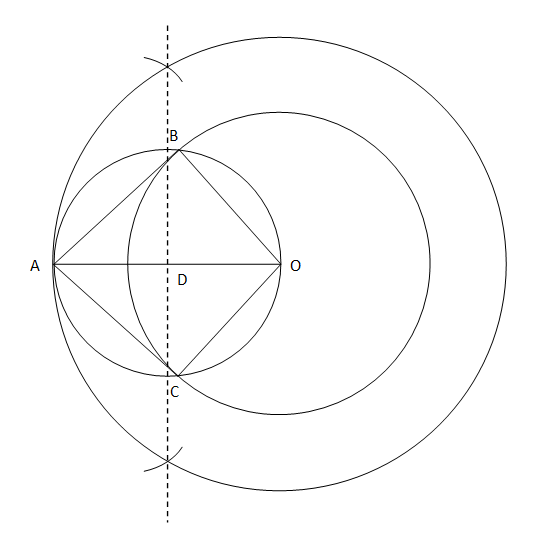
3. Draw a circle of radius 3 cm. Take two points P and Q on one of its extended diameter each at a distance of 7 cm from its centre. Draw tangents to the circle from these two points P and Q. Solution Steps for the construction are as follow:
Justification: We need to connect O with A, B, C and D. ∠A is an angle in a semi-circle subtended by a diameter. Therefore, it will be a right angle. This means that OA will be perpendicular to PA. Since, the radius OA of the circle is perpendicular to the line PA that touches it at one point. Therefore, PA is a tangent to this circle. Similarly, PB, QC, and QD are tangents to this circle. Hence, the construction is justified. 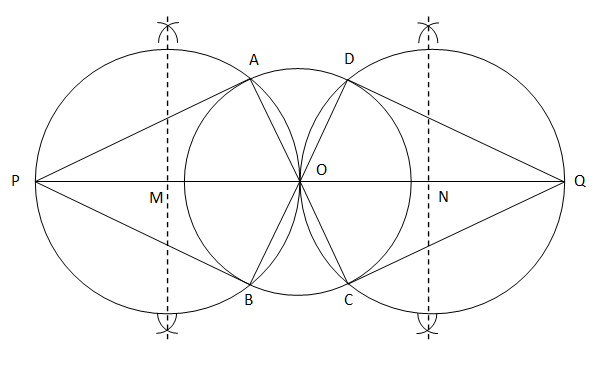
4. Draw a pair of tangents to a circle of radius 5 cm which are inclined to each other at an angle of 60°. Solution Steps for the construction are as follows:
Justification: By construction we have, ∠B = 90° ∠C = 90° And ∠O = 120° OABC forms a quadrilateral, therefore ∠O + ∠A + ∠B + ∠C = 360° 120° + ∠A + 90° + 90° = 360° ∠A + 300° = 360° ∠A = 60° Hence, the construction is justified. 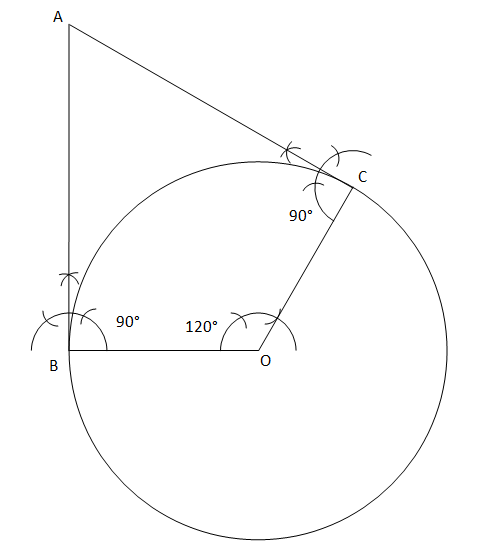
5. Draw a line segment AB of length 8 cm. Taking A as centre, draw a circle of radius 4 cm and taking B as centre, draw another circle of radius 3 cm. Construct tangents to each circle from the centre of the other circle. Solution Steps for the construction are as follows:
Justification: We need to connect A with P and Q and connect B with R and S. ∠P is an angle in a semi-circle subtended by a diameter. Therefore, it will be a right angle. This means that AP will be perpendicular to PB. Since, the radius AP of the circle is perpendicular to the line PB that touches it at one point. Therefore, PB is a tangent to this circle. Similarly, QB is also a tangent to the circle with centre A. Similarly, we can prove that AR and AS are tangents to the circle with the centre B. Hence, the construction is justified. 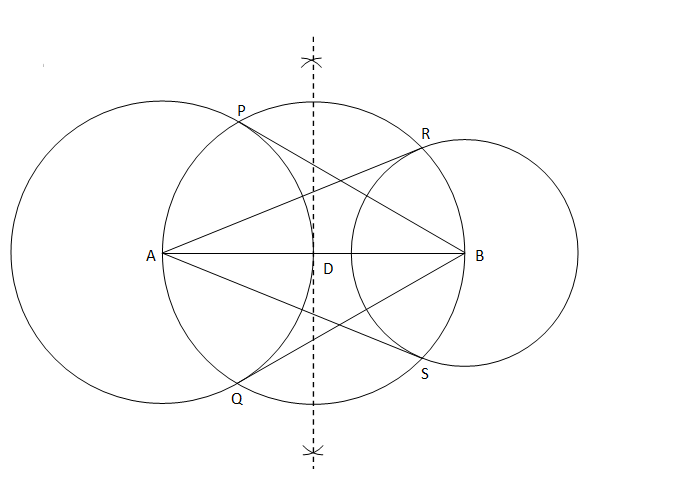
6. Let ABC be a right triangle in which AB = 6 cm, BC = 8 cm and ∠ B = 90°. BD is the perpendicular from B on AC. The circle through B, C, D is drawn. Construct the tangents from A to this circle. Solution Steps for the construction are as follows:
Justification: We need to join O with E. ∠E is an angle in a semi-circle subtended by a diameter. Therefore, it will be a right angle. This means that OE will be perpendicular to AE. Since, the radius OE of the circle is perpendicular to the line AE that touches it at one point. Therefore, AE is a tangent to this circle. Similarly, AB is a tangent to this circle. Hence, the construction is justified. 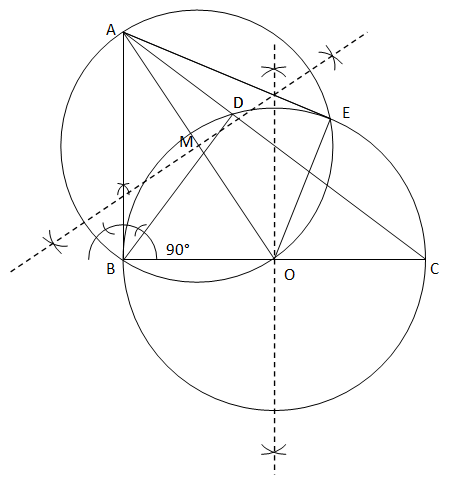
7. Draw a circle with the help of a bangle. Take a point outside the circle. Construct the pair of tangents from this point to the circle. Solution Steps for the construction are as follows:
Justification: We need to join the points Q and R with centre O. ∠Q is an angle in a semi-circle subtended by a diameter. Therefore, it will be a right angle. This means that OQ will be perpendicular to PQ. Since, the radius OQ of the circle is perpendicular to the line PQ that touches it at one point. Therefore, PQ is a tangent to this circle. Similarly, PR is a tangent to this circle. Hence, the construction is justified. 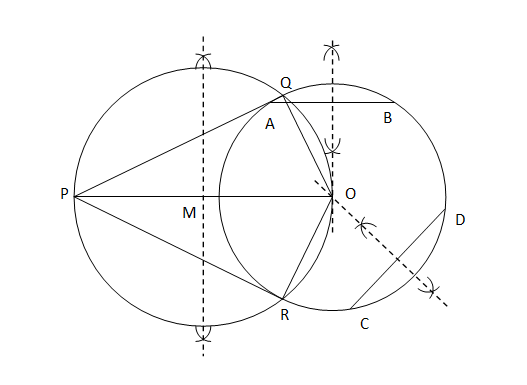
Next TopicClass 10 Maths Chapter 12
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









