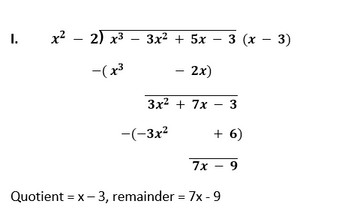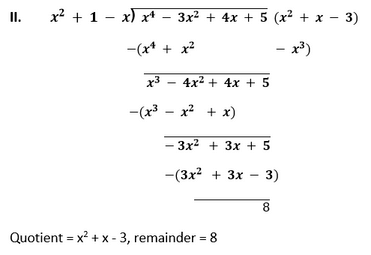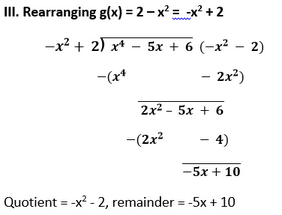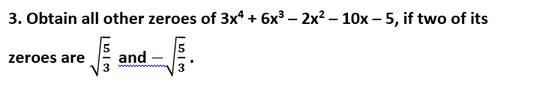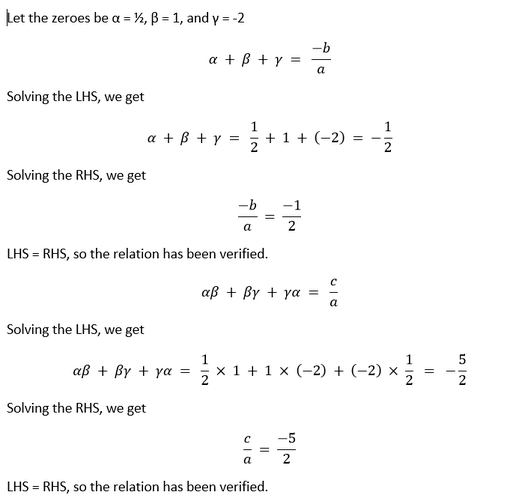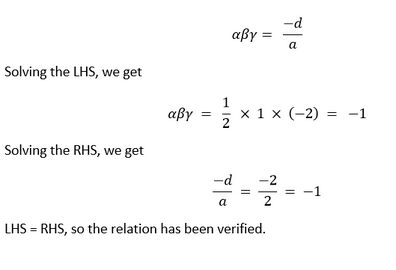NCERT Solutions Class 10 Maths Chapter-2 : Polynomials

Exercise 2.1

1. The graphs of y = p(x) are given in Fig. 2.10 below, for some polynomials p(x). Find the number of zeroes of p(x), in each case.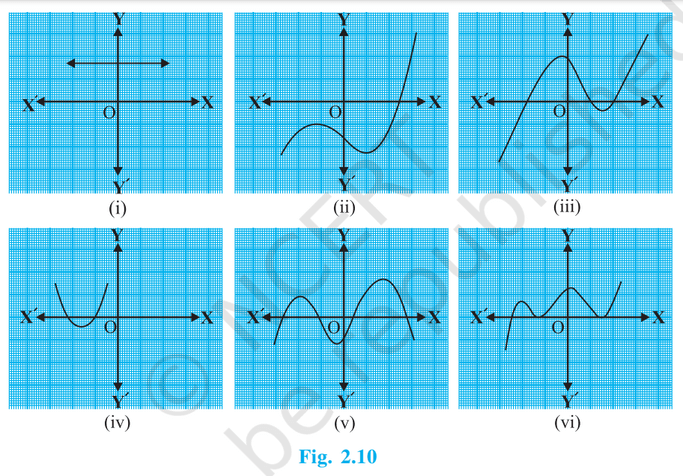

Solution

We can find the number of zeroes p(x) has by counting the points of intersection of the graph on X-axis. By applying this knowledge, we can conclude that the graphs have following numbers of zeroes:

1. No zeroes
2. One zero
3. Three zeroes
4. Two zeroes
5. Four zeroes
6. Three zeroes

2. Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients.

1. x² - 2x - 8
2. 4s² - 4s + 1
3. 6x² - 3 - 7x
4. 4u² + 8u
5. t² - 15
6. 3x² - x - 4

Solution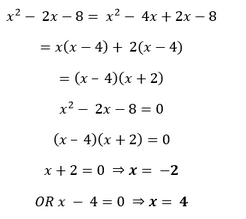

Hence, the given polynomial has two zeroes.

Verification

II.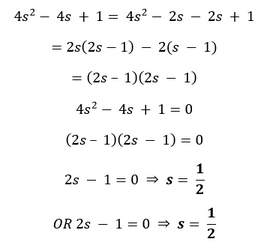

Hence, the given polynomial has two zeroes.

Verification

III.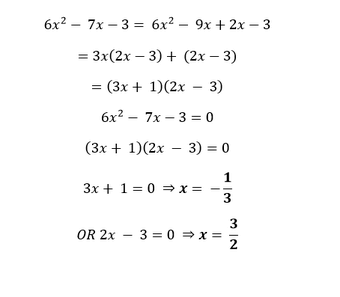

Hence, the given polynomial has two zeroes.

Verification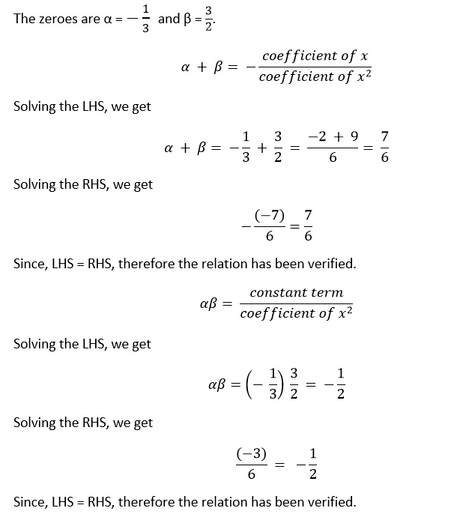

IV.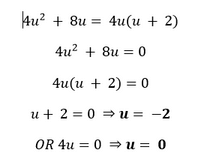

Hence, the given polynomial has two zeroes.

Verification

V.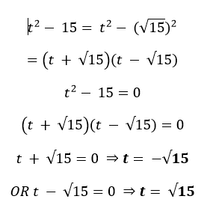

Hence, the given polynomial has two zeroes.

Verification

VI.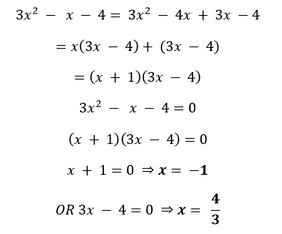

Hence, the given polynomial has two zeroes.

Verification

3. Find a quadratic polynomial each with the given numbers as the sum and product of its zeroes respectively.

1. 1/4 , -1
2. √2, 1/3
3. 0, √5
4. 1, 1
5. -1/4, 1/4
6. 4, 1

Solution

Exercise 2.3

1. Divide the polynomial p(x) by the polynomial g(x) and find the quotient and remainder in each of the following :

1. p(x) = x³ - 3x² + 5x - 3, g(x) = x² - 2
2. p(x) = x⁴ - 3x² + 4x + 5, g(x) = x² + 1 - x
3. p(x) = x⁴ - 5x + 6, g(x) = 2 - x²

Solution

2. Check whether the first polynomial is a factor of the second polynomial by dividing the second polynomial by the first polynomial:

1. t² - 3, 2t⁴ + 3t³ - 2t² - 9t - 12
2. x² + 3x + 1, 3x⁴ + 5x³ - 7x² + 2x + 2
3. x³ - 3x + 1, x⁵ - 4x³ + x² + 3x + 1

Solution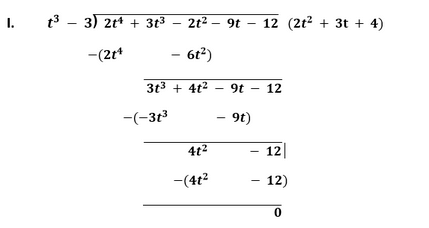

Since, the remainder is zero.

Therefore, first polynomial is a factor of the second polynomial.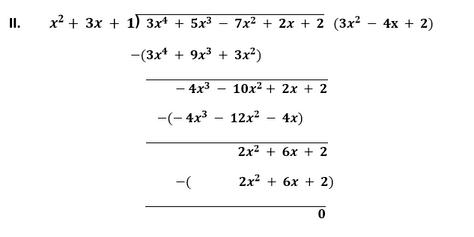

Since, the remainder is zero.

Therefore, first polynomial is a factor of the second polynomial.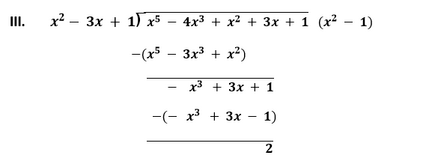

Since, the remainder is not zero.

Therefore, first polynomial is not a factor of the second polynomial.

Solution

Putting the two zeroes in (x - a)(x - b)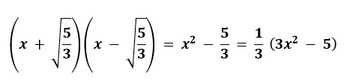

Now, 1/3 and 3x² - 5, both are factors of the given polynomial. If we divide 3x² - 5 by the given polynomial, we get: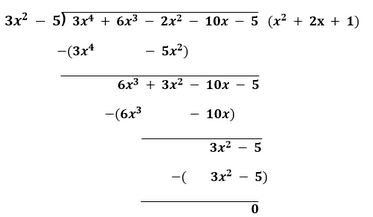

Therefore,

3x⁴ + 6x³ - 2x² - 10x - 5 = (3x² - 5) (x² + 2x + 1)

= (3x² - 5) [(x² + x + x + 1)]

= (3x² - 5) [x(x + 1) + 1(x + 1)]

= (3x² - 5) (x + 1) (x + 1)

When (x + 1) = 0 � x = -1 and when (x + 1) = 0 � x = -1.

Hence, the remaining two zeroes of the given polynomial are -1 and -1.

4. On dividing x³ - 3x² + x + 2 by a polynomial g(x), the quotient and remainder were x - 2 and -2x + 4, respectively. Find g(x).

Solution

We know that,

p(x) = g(x) × Quotient + Remainder

Therefore,

x³ - 3x² + x + 2 = g(x) × (x - 2) + (-2x + 4)

x³ - 3x² + x + 2 + 2x - 4= g(x) × (x - 2)

x³ - 3x² + 3x - 2 = g(x) × (x - 2)

On dividing x - 2 with x³ - 3x² + 3x - 2, we get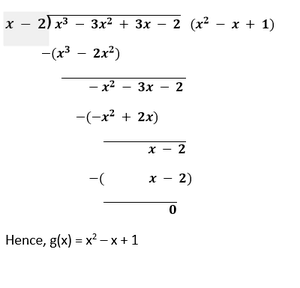

5. Give examples of polynomials p(x), g(x), q(x) and r(x), which satisfy the division algorithm and:

1. deg p(x) = deg q(x)
2. deg q(x) = deg r(x)
3. deg r(x) = 0

Solution

I. p(x) = 8x² + 4x + 2

q(x) = 4x² + 2x + 1

g(x) = 2

r(x) = 0

II. p(x) = x³ - 3x² + 5x - 3

q(x) = x - 3

g(x) = x² - 2

r(x) = 7x - 9

III. p(x) = x³ - x² + 2x + 3

q(x) = x - 1

g(x) = x² + 2

r(x) = 5

Exercise 2.4 (Optional)

1. Verify that the numbers given alongside of the cubic polynomials below are their zeroes. Also verify the relationship between the zeroes and the coefficients in each case:

1. 2x³ + x² - 5x + 2; 1/2 , 1, - 2
2. x³ - 4x² + 5x - 2; 2, 1, 1

Solution

I. Comparing the given polynomial with p(x) = ax3 + bx2 + cx +d, we get

a = 2, b = 1, c = -5, d = 2

Now we will check if the given numbers are zeroes of the given polynomial by substituting them for x.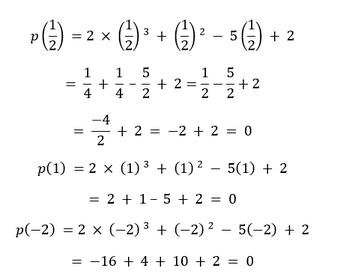

Hence, the given numbers are the zeroes of the given polynomial.

II. Comparing the given polynomial with p(x) = ax3 + bx2 + cx +d, we get

a = 1 , b = -4, c = 5, d = -2

Now we will check if the given numbers are zeroes of the given polynomial by substituting them for x.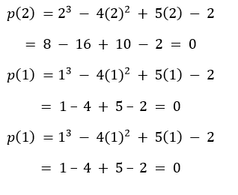

Hence, the given numbers are the zeroes of the given polynomial.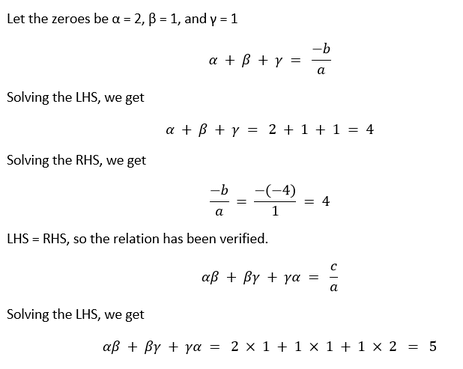

2. Find a cubic polynomial with the sum, sum of the product of its zeroes taken two at a time, and the product of its zeroes as 2, -7, -14 respectively.

Solution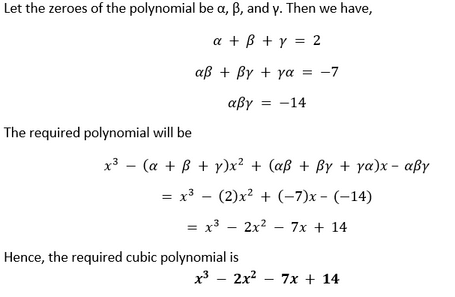

3. If the zeroes of the polynomial x3 - 3x2 + x + 1 are a - b, a, a + b, find a and b.

Solution

Comparing the given polynomial with Ax³ + Bx² + Cx + D, we get

A = 1, B = -3, C = 1, and D = 1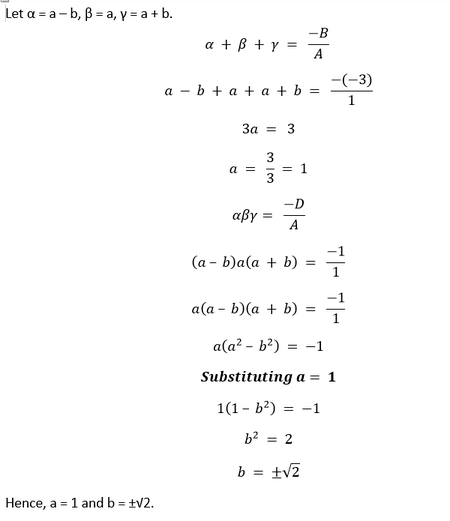

4. If two zeroes of the polynomial x⁴ - 6x³ - 26x² + 138x - 35 are 2 � √3, find other zeroes.

Solution

Substituting the two zeroes in (x - a) (x - b)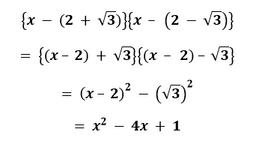

Now, x² - 4x + 1 is a factor of the given polynomial. If we divide x² - 4x + 1 by the given polynomial, we get: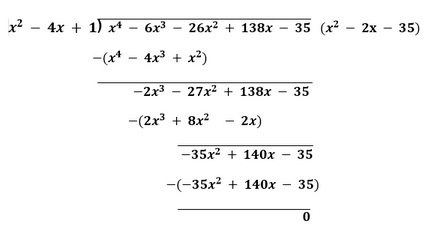

Therefore,

x⁴ - 6x³ - 26x² + 138x - 35 = (x² - 4x + 1) (x² -� 2x - 35)

= (x² - 4x + 1) (x² - 7x + 5x - 35)

= (x² - 4x + 1) {x(x - 7) + 5(x - 7)}

= (x² - 4x + 1) (x - 7) (x + 5)

Hence, the two remaining zeroes will be 7 and -5.

5. If the polynomial x⁴ - 6x³ + 16x² - 25x + 10 is divided by another polynomial x² - 2x + k, the remainder comes out to be x + a, find k and a.

Solution

First, we need to divide x⁴ - 6x³ + 16x² - 25x + 10 by x² - 2x + k and find out the remainder.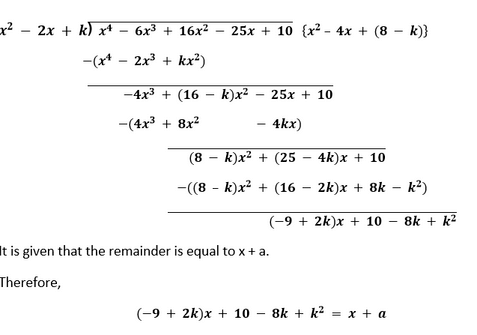

Upon comparing the coefficients, we get two equations

First equation -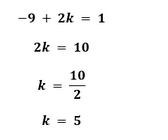

Second equation -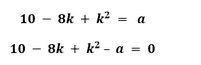

Substitute k = 5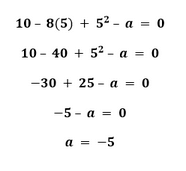

Hence, k = 5 and a = -5.