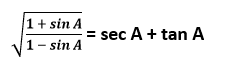Maths Solution Class 10 Chapter 8: Introduction to TrigonometryExercise 8.11. In ∆ ABC, right-angled at B, AB = 24 cm, BC = 7 cm. Determine :
Solution By applying Pythagoras Theorem in ABC, we get AC2 = AB2 + BC2 AC2 = 242 + 72 AC2 = 576 + 49 AC2 = 625 AC = 25 cm I. sin A = Opposite Side/ Hypotenuse = BC/AC = 7/25 cos A = Adjacent Side/ Hypotenus = AB/AC = 24/25 II. sin C = Opposite Side/ Hypotenuse = AB/AC = 24/25 cos C = Adjacent Side/ Hypotenus = BC/AC = 7/25 2. In Fig. 8.13, find tan P - cot R. 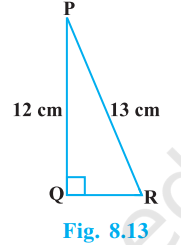
Solution By applying Pythagoras Theorem in PQR, we get PR2 = PQ2 + QR2 QR2 = PR2 - PQ2 QR2 = 132 - 122 QR2 = 169 - 144 QR2 = 25 QR = 5 cm tan P = Opposite side/ Adjacent Side = QR/PQ = 5/12 cot R = Adjacent side/ Opposite Side = QR/PQ = 5/12 tan P - cot R = 5/12 - 5/12 = 0 3. If sin A = 3/4, calculate cos A and tan A. Solution sin A = Opposite side/ Hypotenuse 3/4 = Opposite side/ Hypotenuse Let Opposite side = 3x and Hypotenuse = 4x By using the Pythagoras Theorem: (4x)2 = (Side adjacent to A)2 + (3x)2 16x2 = (Side adjacent to A)2 + 9x2 7x2 = (Side adjacent to A)2 Side adjacent to A = x√7 cos A = Adjacent side/ Hypotenuse = x√7/4x = √7/4 tan A = Opposite side/ Hypotenuse = 3x/x√7 = 3/√7 Hence, cos A = √7/4 and tan A = 3/√7. 4. Given 15 cot A = 8, find sin A and sec A. Solution 15 cot A = 8 cot A = 8/15 Adjacent Side/ Opposite side = 8/15 Let the side adjacent to A be 8x and let the side opposite to A be 15x. By Pythagoras Theorem: Hypotenuse2 = (8x)2 + (15x)2 Hypotenuse2 = 64x2 + 225x2 Hypotenuse2 = 289x2 Hypotenuse = 17x Now, sin A = Opposite Side/ Hypotenuse = 15x/17x = 15/17 sec A = Hypotenuse/ Adjacent Side = 17x/8x = 17/8 Hence, sin A = 15/17 and sec A = 17/8. 5. Given sec θ = 13/12, calculate all other trigonometric ratios. Solution sec θ = Hypotenuse/ Adjacent side 13/12 = Hypotenuse/ Adjacent side Let Hypotenuse = 13x and Adjacent side = 12x By Pythagoras Theorem: (13x)2 = (12x)2 + (Opposite side)2 169x2 = 144x2 + (Opposite side)2 25x2 = (Opposite side)2 5x = Opposite side Now, sin θ = Opposite side/ Hypotenuse = 5x/13x = 5/13 cos θ = Adjacent side/ Hypotenuse = 12x/13x = 12/13 tan θ = Opposite side/ Adjacent side = 5x/12x = 5/12 cosec θ = Hypotenuse/ Opposite side = 13x/5x = 13/5 cot θ = Adjacent side/ Opposite side = 12x/5x = 12/5 6. If ∠ A and ∠ B are acute angles such that cos A = cos B, then show that ∠ A = ∠ B. Solution Let the triangle be ABC, with a line CD ? AB. cos A = cos B AD/AC = BD/BC AD/BD = AC/BC Let AD/BD = AC/BC = x Therefore, AD = xBD and AC = xBC By applying Pythagoras Theorem in CAD, we get AC2 = CD2 + AD2 CD2 = AC2 - AD2 By applying Pythagoras Theorem in CBD, we get BC2 = CD2 + BD2 CD2 = BC2 - BD2 AC2 - AD2 = BC2 - BD2 (xBC)2 - (xBD)2 = BC2 - BD2 x2(BC2 - BD2) = BC2 - BD2 x2 = 1 x = 1 Therefore, AC/BC = x = 1 AC = BC This implies that ∠ A = ∠ B as angles opposite to equal sides of a triangle are also equal. Hence, proved. 7. If cot θ = 7/8, evaluate :
Solution cot θ = 7/8 Adjacent side/ Opposite side = 7/8 Let adjacent side be 7x and opposite side be 8x. By using Pythagoras Theorem: Hypotenuse2 = Adjacent side2 + Opposite side2 Hypotenuse2 = (7x)2 + (8x)2 Hypotenuse2 = 49x2 + 64x2 Hypotenuse2 = 113x2 Hypotenuse = x√113 sin θ = Opposite side/ Hypotenuse = 8x/x√113 = 8/√113 cos θ = Adjacent side/ Hypotenuse = 7x/x√113 = 7/√113 I. (1 + sin θ)(1 - sin θ)/(1 + cos θ)(1 - cos θ) = (1 + 8/√113)(1 - 8/√113)/(1 + 7/√113)(1 - 7/√113) = 12 - (8/√113)2 /12 - (7/√113)2 = 49/64 II. cot2 θ = (7/8)2 = 49/64 8. If 3 cot A = 4, check whether (1 - tan2 A)/(1 + tan2 A) = cos2 A - sin2A or not. Solution 3 cot A = 4 cot A = 4/3 Adjacent side/ Opposite side = 4/3 Let adjacent side = 4x and opposite side = 3x By using Pythagoras Theorem: Hypotenuse2 = Adjacent side2 + Opposite side2 Hypotenuse2 = (4x)2 + (3x)2 Hypotenuse2 = 16x2 + 9x2 Hypotenuse2 = 25x2 Hypotenuse = 5x sin A = Opposite side/ Hypotenuse = 3x/5x = 3/5 cos A = Adjacent side/ Hypotenuse = 4x/5x = 4/5 tan A = Opposite side/ Adjacent side = 3x/4x = 3/4 Now, LHS of the given relation: 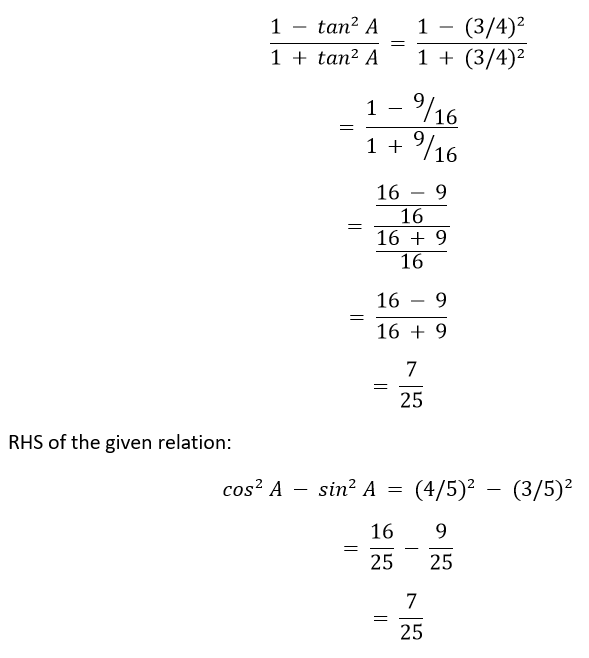
Therefore, LHS = RHS. Hence, proved. 9. In triangle ABC, right-angled at B, if tan A = 1/√3, find the value of:
Solution tan A = 1/√3 Opposite side/ Adjacent side = 1/√3 Let BC = x and AB = x√3 By using Pythagoras Theorem: AC2 = AB2 + BC2 AC2 = (x√3)2 + (x)2 AC2 = x2 + 3x2 AC2 = 4x2 AC = 2x sin A = Opposite side/ Hypotenuse = BC/AC = x/2x = 1/2 cos A = Adjacent side/ Hypotenuse = AB/AC = x√3/2x = √3/2 sin C = AB/AC = x√3/2x = √3/2 cos C = BC/AC = x/2x = 1/2 I. sin A cos C + cos A sin C = (1/2)(1/2) + (√3/2)(√3/2) = ¼ + ¾ = 4/4 = 1 II. cos A cos C - sin A sin C = (1/2)(√3/2) - (1/2)(√3/2) = √3/4 - √3/4 = 0 10. In ∆ PQR, right-angled at Q, PR + QR = 25 cm and PQ = 5 cm. Determine the values of sin P, cos P and tan P. Solution PR + QR = 25 PR = 25 - QR By applying Pythagoras Theorem in PQR, we get PR2 = PQ2 + QR2 (25 - QR)2 = 52 + QR2 252 + QR2 - 2(25)(QR) = 25 + QR2 625 - 50QR = 25 600 = 50QR QR = 12 cm Now, PR = 25 - QR = 25 - 12 = 13 cm sin P = QR/PR = 12/13 cos P = PQ/PR = 5/13 tan P = QR/PQ = 12/5 11. State whether the following are true or false. Justify your answer.
Solution I. The given statement is false. For a triangle ABC right angled at B: tan A = Opposite side/ Adjacent side It is possible to have side opposite to the angle greater than the side adjacent to it, which will make tan A greater than 1. Example side lengths of ABC - 3 units, 4 units, and 5 units II. The given statement is true. Let there be a triangle ABC right angled at B. sec A = 12/5 AC/AB = 12/5 Let AC = 12x and AB = 5x By Pythagoras theorem: AC2 = AB2 + BC2 (12x)2 = (5x)2 + BC2 144x2 = 25x2 + BC2 119x2 = BC2 Therefore it satisfies the Pythagoras Theorem. Hence, sec A = 12/5 is possible. III. The given statement is false. cos A is the abbreviation used for cosine of angle A. IV. The given statement is false. cot A is not a product of cot and A. It means cotangent of angle A. V. The given statement is false. sin A = Opposite side/ Hypotenuse For sin A to be 4/3, side of the triangle needs to be greater than the hypotenuse, which is impossible as hypotenuse is the longest side of a right angled triangle. Exercise 8.21. Evaluate the following :
Solution I. sin 60° = √3/2 cos 30° = √3/2 sin 30° = 1/2 cos 60° = 1/2 sin 60° cos 30° + sin 30° cos 60° = (√3/2) × (√3/2) + (1/2) × (1/2) = 3/4 + 1/4 = 4/4 = 1 II. tan 45° = 1 sin 60° = √3/2 cos 30° = √3/2 2 tan2 45° + cos2 30° - sin2 60° = 2 × (1)2 + (√3/2)2 - (√3/2)2 = 2 + 3/4 - 3/4 = 2 III. cos 45° = 1/√2 sec 30° = 2/√3 cosec 30° = 2 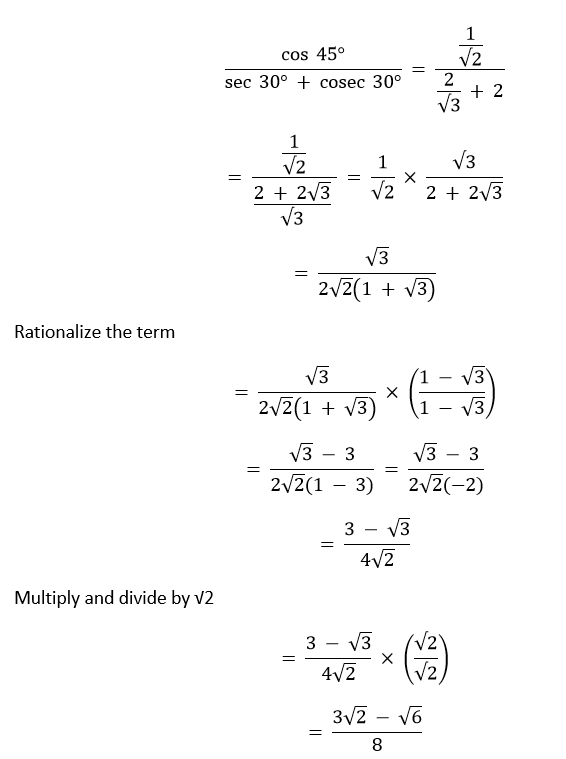
IV. sin 30° = 1/2 tan 45° = 1 cosec 60° = 2/√3 sec 30° = 2/√3 cos 60° = 1/2 cot 45° = 1 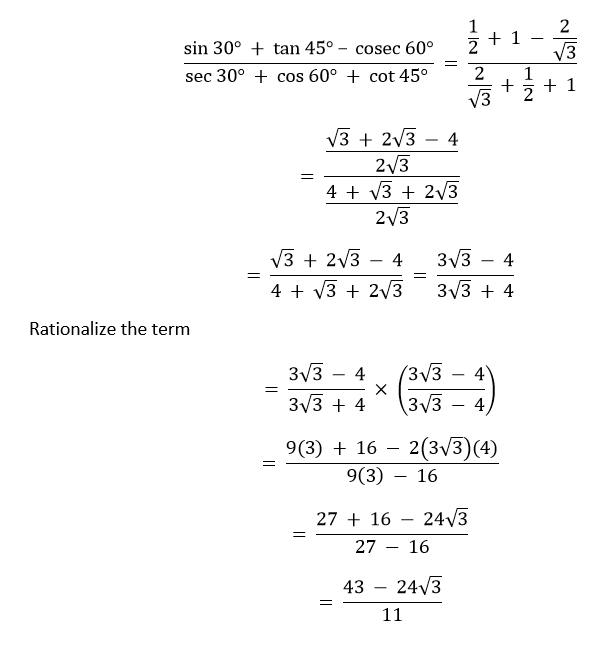
V. cos 60° = 1/2 sec 30° = 2/√3 tan 45° = 1 sin 30° = 1/2 cos 30° = √3/2 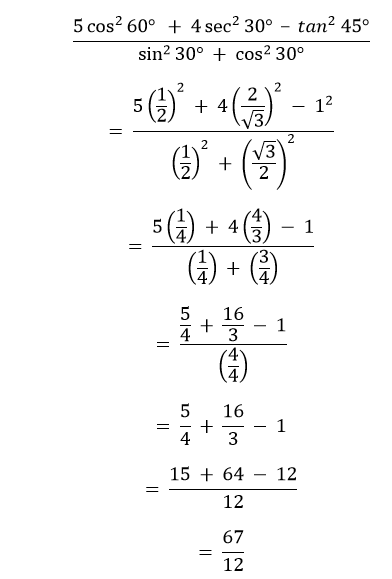
2. Choose the correct option and justify your choice :
Solution I. 2 tan 30°/(1 + tan2 30°) = 2(1/√3)/(1 + 1/√32) = (2/√3)/(1 + 1/3) = (2/√3)/(4/3) = 2√3/4 = √3/2 = sin 60° Hence, (A) is the correct answer. II. (1 - tan2 45°)/(1 + tan2 45°) = (1 - 12)/(1 + 12) = (1 - 1)/(1 + 1) = 0/2 = 0 Hence, (D) is the correct answer. III. Put A = 0° sin 2A = sin 0° = 0 2 sin A = 2 sin 0° = 2 (0) = 0 Hence, (A) is the correct answer. IV. 2 tan 30°/(1 - tan2 30°) = 2(1/√3)/(1 - 1/√32) = (2/√3)/(1 - 1/3) = (2/√3)/(2/3) = 3/√3 = √3 = tan 60° Hence, (C) is the correct answer. 3. If tan (A + B) = √3 and tan (A - B) = 1/√3; 0° < A + B ? 90°; A > B, find A and B. Solution tan (A + B) = √3 We know that tan 60° = √3. Therefore, tan (A + B) = tan 60° A + B = 60 tan (A - B) = 1/√3 We know that tan 30° =1/√3. Therefore, tan (A - B) = tan 30° A - B = 30 Add the obtained equations A + B + A - B = 60 + 30 2A = 90 A = 45 Now, to find B: A - B = 30 45 - B = 30 B = 15 Hence, A = 45° and B = 15° 4. State whether the following are true or false. Justify your answer.
Solution I. If we put A = 30° and B = 60°, we will get: LHS = sin (A + B) = sin (30° + 60°) = sin 90° = 1 RHS = sin A + sin B = sin 30° + sin 60° = 1/2 + √3/2 = (√3 + 1)/2 Therefore, LHS ? RHS. Hence, the give statement is false. II. sin 0° = 0 sin 30° = 1/2 sin 45° = 1/√2 sin 60° = √3/2 sin 90° = 1 Therefore, the value of sin θ increases with the value of θ. Hence, the given statement is true. III. cos 0° = 1 cos 30° = √3/2 cos 45° = 1/√2 cos 60° = 1/2 cos 90° = 0 Therefore, the value of cos θ decreases with the value of θ. Hence, the given statement is false. IV. sin 0° = 0 while cos 0° = 1 Hence, the given statement is false. V. cot A = cot 0° = cos 0°/sin 0° = 1/0 = Undefined Hence, the given statement is true. Exercise 8.31. Evaluate :
Solution I. sin 18°/cos 72° = cos (90° - 18°)/cos 72° = cos 72°/ cos 72° = 1 II. tan 26°/cot 64° = cot (90° - 24°)/cot 64° = cot 64°/ cot 64° = 1 III. cos 48°/sin 42° = sin (90° - 48°)/sin 42° = sin 42°/ sin 42° = 1 IV. cosec 31°/sec 59° = sec (90° - 31°)/sec 59° = sec 59°/ sec 59° = 1 2. Show that :
Solution I. tan 48° tan 23° tan 42° tan 67° = tan (90° - 42°) tan (90° - 67°) tan 42° tan 67° = cot 42° cot 67° tan 42° tan 67° = (cot 42° tan 42°) (cot 67° tan 67°) = 1 × 1 = 1 Hence, proved. II. cos 38° cos 52° - sin 38° sin 52° = cos (90° - 52°) cos (90°-38°) - sin 38° sin 52° = sin 52° sin 38° - sin 38° sin 52° = 0 Hence, proved. 3. If tan 2A = cot (A - 18°), where 2A is an acute angle, find the value of A. Solution We know that, tan 2A = cot (90° - 2A) as 2A is an acute angle. Therefore, tan 2A = cot (A - 18°) cot (90° - 2A) = cot (A - 18°) 90° - 2A = A - 18° 108° = 3A A = 36° Hence, A = 36°. 4. If tan A = cot B, prove that A + B = 90°. Solution tan A = cot B tan A = tan (90° - B) A = 90° - B Therefore, A + B = 90° Hence, proved. 5. If sec 4A = cosec (A - 20°), where 4A is an acute angle, find the value of A. Solution We know that, sec 4A = cosec (90° - 4A) as 4A is an acute angle. Therefore, sec 4A = cosec (A - 20°) cosec (90° - 4A) = cosec (A - 20°) 90° - 4A = A - 20° 110° = 5A A = 22° Hence, A = 22°. 6. If A, B and C are interior angles of a triangle ABC, then show that sin ((B + C)/2) = cos A/2 Solution Since, A, B and C are interior angles of a triangle. Therefore, A + B + C = 180° B + C = 180° - A Divide both sides by 2 (B + C)/2 = (180° - A)/2 (B + C)/2 = (90° - A/2) Taking sin on both sides, we get sin ((B + C)/2) = sin (90° - A/2) We know that sin (90° - ?) = cos (?) Therefore, sin ((B + C)/2) = cos (A/2) Hence, proved. 7. Express sin 67° + cos 75° in terms of trigonometric ratios of angles between 0° and 45°. Solution sin 67° = cos (90° - 67°) = cos 23° cos 75° = sin (90° - 75°) = sin 25° Hence, sin 67° + cos 75° can be expressed as cos 23° + sin 25° Exercise 8.41. Express the trigonometric ratios sin A, sec A and tan A in terms of cot A. Solution We know that, cosec2 A- cot2 A = 1 cosec2 A = 1 + cot2 A (1/sin2 A) = 1 + cot2 A as cosec is the inverse of sin function sin2 A = 1/(1 + cot2 A) Square root on both sides, sin A = ±1/√(1 + cot2 A) Hence, sin A in terms of cot A is ±1/√(1 + cot2 A). Now, sin2 A = 1/(1 + cot2 A) 1 - cos2 A = 1/(1 + cot2 A) as sin2 A + cos2 A = 1 cos2 A = 1 - 1/(1 + cot2 A) cos2 A = (1 - 1 + cot2 A)/(1 + cot2 A) 1/sec2 A = (cot2 A)/(1 + cot2 A) as sec is the inverse of cos function sec2 A = (1 + cot2 A)/cot2 A Square root on both sides, secA = ±√(1 + cot2 A)/cotA Hence, sec A in terms of cot A is ±√(1 + cot2 A)/cot A. We know that, tan A = sin A/cos A Reciprocal both sides, 1/tan A = cos A/sin A 1/tan A = cot A tan A = 1/cot A Hence, tan A in terms of cot A is 1/cot A. 2. Write all the other trigonometric ratios of ∠ A in terms of sec A. Solution We know that cos A is inverse of sec A. Therefore, sec A = 1/cos A cos A = 1/sec A Hence, cos A in terms of sec A is 1/sec A. We know that, cos2 A + sin2 A = 1 sin2 A = 1 - cos2 A sin2 A = 1 - (1/sec2 A) sin2 A = (sec2 A - 1)/sec2 A sin A = ±√(sec2 A - 1)/sec A Hence, sin A in terms of sec A is ±√(sec2 A - 1)/sec A. sin A = 1/cosec A cosec A = 1/sin A cosec A = ±1/√(sec2 A - 1)/sec A Hence, cosec A in terms of sec A is ±1/√(sec2 A - 1)/sec A. We know that, sec2 A - tan2 A = 1 tan2 A = sec2 A - 1 tan A = ±√(sec2 A - 1) Hence, tan A in terms of sec A is ±√(sec2 A - 1). tan A = 1/cot A cot A = 1/tan A cot A = 1/±√(sec2 A - 1) Hence, cot A in terms of sec A is ±1/√(sec2 A - 1). 3. Evaluate:
Solution I. (sin2 63° + sin2 27°)/(cos2 17° + cos2 73°) = (cos2 (90° - 63°) + sin2 27°)/(cos2 17° + sin2 (90° - 73°)) = (cos2 27° + sin2 27°)/(cos2 17° + sin2 17°) We know that, cos2 A + sin2 A = 1. Therefore, (cos2 27° + sin2 27°)/(cos2 17° + sin2 17°) = 1/1 = 1 II. sin 25° cos 65° + cos 25° sin 65° = sin 25° sin (90° - 65°) + cos 25° cos (90° - 65°) = sin 25° sin 25° + cos 25° cos 25° = sin2 25° + cos2 25° We know that, cos2 A + sin2 A = 1. Therefore, sin2 25° + cos2 25° = 1 4. Choose the correct option. Justify your choice.
Solution I. 9 sec2 A - 9 tan2 A = 9(sec2 A - tan2 A) We know that sec2 θ - tan2 θ = 1. Therefore, 9(sec2 A - tan2 A) = 9 (1) = 9 Hence, (B) is the correct answer. II. (1 + tan θ + sec θ) (1 + cot θ - cosec θ) = (1 + sin θ/cos θ + 1/cos θ)(1 + cos θ/sin θ - 1/sin θ) = (sin θ + cos θ + 1)/cos θ × (sin θ + cos θ - 1)/sin θ = (cos θ + sin θ)2 - 12)/cos θ sin θ = (cos2 θ + sin2 θ + 2cos θ sin θ - 1)/cos θ sin θ We know that, cos2 A + sin2 A = 1. Therefore, (cos2 θ + sin2 θ + 2cos θ sin θ - 1)/cos θ sin θ = (1 + 2cos θ sin θ - 1)/cos θ sin θ = 2cos θ sin θ/cos θ sin θ = 2 Hence, (C) is the correct answer. III. (sec A + tan A) (1 - sin A) = (1/cos A + sin A/cos A) (1 - sin A) = (1 + sin A)(1 - sin A)/cos A = (12 - sin2 A)/cos A = (1 - sin2 A)/cos A We know that sin2 A - cos2 A = 1. Therefore, (1 - sin2 A)/cos A = cos2 A/cos A = cos A Hence, (D) is the correct answer. IV. (1 + tan2 A)/(1 + cot2 A) = (1 + 1/cot2 A)/(1 + cot2 A) = (cot2 A + 1)/cot2 A(1 + cot2 A) = 1/cot2 A = tan2 A Hence, (D) is the correct answer. 5. Prove the following identities, where the angles involved are acute angles for which the expressions are defined.
Solution I. (cosec θ - cot θ)2 = (1 - cos θ)/(1 + cos θ) = (cosec2 θ + cot2 θ - 2cosec θ cot θ) = (1/sin2 θ + cos2 θ/sin2 θ - 2cos θ /(sin2 θ)) = (1 + cos2 θ - 2cos θ)/sin2 θ = (12 + cos2 θ - 2(1)cos θ)/sin2 θ = (1 - cos θ)2/(sin2 θ) Since, sin2 A + cos2 A = 1. Therefore, (1 - cos θ)2/(sin2 θ) = (1 - cos θ)2/(1 - cos2 θ) = (1 - cos θ)2/(1 - cos θ)(1 + cos θ) = (1 - cos θ)/(1 + cos θ) Hence, proved. II. (cos A/(1 + sin A)) + ((1 + sin A)/cos A) = (cos2 A + (1 + sin A)2)/(1 + sin A)cos A = (cos2 A + sin2 A + 1 + 2sin A)/(1 + sin A)cos A Since, sin2 a + cos2 a = 1. Therefore, (cos2 A + sin2 A + 1 + 2sin A)/(1 + sin A)cos A = (1 + 1 + 2sin A)/(1 + sin A)cos A = 2(1 + sin A)/(1 + sin A)cos A = 2/cos A = 2 sec A Hence, proved. III. tan θ/(1 - cot θ) + cot θ/(1 - tan θ) = sin θ/cos θ(1 - cos θ/sin θ) + cos θ/sin θ(1 - sin θ/cos θ) = sin θ/cos θ((sin θ - cos θ)/sin θ) + cos θ/sin θ((cos θ - sin θ)/cos θ) = sin2 θ/(sin θ - cos θ)cos θ + cos2 θ/(cos θ - sin θ)sin θ = sin2 θ/(sin θ - cos θ)cos θ - cos2 θ/(sin θ - cos θ)sin θ = 1/(sin θ - cos θ)[sin2 θ/cos θ - cos2 θ/sin θ] = [sin2 θ/cos θ - cos2 θ/sin θ]/(sin θ - cos θ) = [(sin3 θ - cos3 θ)/sin θ cos θ]/(sin θ - cos θ) = [(sin θ - cos θ)(sin2 θ + cos2 θ + sin θ cos θ)/sin θ cos θ]/(sin θ - cos θ) = (sin2 θ + cos2 θ + sin θ cos θ)/sin θ cos θ Since, sin2 a + cos2 a = 1. Therefore, (sin2 θ + cos2 θ + sin θ cos θ)/sin θ cos θ = (1 + sin θ cos θ)/sin θ cos θ = 1/sin θ cos θ + sin θ cos θ/sin θ cos θ = cosec θ sec θ + 1 = 1 + sec θ cosec θ Hence, proved. IV. LHS = (1 + sec A)/sec A = (1 + 1/cos A)/(1/cos A) = ((cos A + 1)/cos A)/(1/cos A) = cos A + 1 RHS = sin2 A/(1 - cos A) = (1 - cos2 A)/(1 - cos A) = (12 - cos2 A)/(1 - cos A) = (1 - cos A)(1 + cos A)/(1 - cos A) = cos A + 1 LHS = RHS Hence, proved. V. Divide the numerator and denominator by sin A [(cos A - sin A + 1)/sin A]/[(cos A + sin A - 1)/sin A] = (cot A - 1 + cosec A)/(cot A + 1 - cosec A) Since, cosec2 A = 1 + cot2 A. Therefore, 1 = cosec2 A - cot2 A. (cot A - 1 + cosec A)/(cot A + 1 - cosec A) = (cot A - (cosec2 A - cot2 A) + cosec A)/(cot A + 1 - cosec A) = (cot A + cosec A - (cosec A + cot A)(cosec A - cot A))/(cot A + 1 - cosec A) = (cosec A + cot A)(1 + cot A - cosec A)/(cot A + 1 - cosec A) = cosec A + cot A Hence, proved. VI. 
Since, sec2 A - tan2 A = 1. Therefore, = (sec A + tan A)/1 = sec A + tan A VII. (sin θ - 2sin3 θ)/(2cos3 θ - cos θ) = sin θ (1 - 2sin2 θ)/cos θ (2cos2 θ - 1) Since, sin2 θ = 1 - cos2 θ. Therefore, sin θ (1 - 2sin2 θ)/cos θ (2cos2 θ - 1) = sin θ (1 - 2(1 - cos2 θ))/cos θ (2cos2 θ - 1) = sin θ (1 - 2 + 2cos2 θ)/cos θ (2 cos2 θ - 1) = sin θ (-1 + 2cos2 θ)/cos θ (2 cos2 θ - 1) = sin θ/cos θ = tan θ Hence, proved. VIII. (sin A + cosec A)2 + (cos A + sec A)2 = sin2 A + cosec2 A + 2sin A cosec A + cos2 A + sec2 A + 2cos A sec A Since, cosec2 A = 1 + tan2 A and sec2 A = 1 + cot2 A. Therefore, sin2 A + cosec2 A + 2sin A cosec A + cos2 A + sec2 A + 2cos A sec A = sin2 A + 1 + tan2 A + 2sin A cosec A + cos2 A + 1 + cot2 A + 2cos A sec A = 2 + tan2 A + cot2 A + sin2 A + cos2 A + 2sin A (1/sin A) + 2cos A (1/cos A) Since, sin2 A + cos2 A = 1. Therefore, = 2 + tan2 A + cot2 A + 1+ 2 + 2 = 7 + tan2 A + cot2 A Hence, proved. IX. LHS = (cosec A - sin A)(sec A - cos A) = (1/sin A - sin A)(1/cos A - cos A) = [(1 - sin2 A)/sin A][(1 - cos2 A)/cos A] Since, sin2 a + cos2 a = 1. Therefore, [(1 - sin2 A)/sin A][(1 - cos2 A)/cos A] = [(cos2 A)/sin A][(sin2 A)/cos A] = (cos A)(sin A) = sin A cos A RHS = 1/(tan A + cot A) = 1/(sin A/cos A + cos A/sin A) = 1/[(sin2 + cos2 A)/sin A cos A] = 1/(1/sin A cos A) = sin A cos A Therefore, LHS = RHS Hence, proved. X. Part (i) (1 + tan2 A/1 + cot2 A) = (1 + tan2 A)/(1 + 1/tan2 A) = (1 + tan2 A)/[(tan2 A + 1)/tan2 A] = tan2 A (1 + tan2 A)/(tan2 A + 1) = tan2 A Part (ii) (1 - tan A)2/(1 - cot A)2 = (1 - tan A)2/(1 - 1/tan A)2 = (1 - tan A)2/((tan A - 1)/tan A)2 = (1 - tan A)2/[(tan A - 1)2/tan2 A] = tan2 A (1 - tan A)2/(-(1 - tan A))2 = tan2 A (1 - tan A)2/(1 - tan A)2 = tan2 A Hence, proved.
Next TopicClass 10 Maths Chapter 9
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share