NCERT Solutions for Class 11 Science Physics Chapter 2 - Units and MeasurementsStudents can use this NCERT Solutions for Class 11 Physics to understand this topic better. The most useful study materials for Class 11 Physics Chapter 2 Units and Measurements are NCERT Solutions, which may help students grasp the key concepts and perform well on exams. These solutions properly provide the answers to the textbook questions. 
Following the most recent CBSE Syllabus 2022-23, Chapter 2 of the NCERT Solutions for Class 11 Physics primarily aids in understanding the foundations of units and measurements. Most things we do in daily life depend on this. Thus pupils must understand it well. Everything is based on measurements and units, from purchasing milk in the morning to the pounds of bread required for breakfast or kilograms of rice required for lunch. Students who need help understanding the important ideas in this chapter can use the Physics NCERT Solutions for Class 11. NCERT Solutions Class 11 Physics Chapter 2 Units and MeasurementsExercise: Page No. 35Question 2.1: Fill in the blanks.
Answer: a.) Volume of a cube = (side)3 (1 cm)3 = (1 × 10-2 m)3 = 1 × 10-6 m b.) Given that, r = 2 cm = 20 mm h = 10 cm = 100 mm Total surface area, S = 2πrh + 2πr2 S = 2πr(h + r) S = 2 × 3.14 × 20(100+20) S = 125.6 × 120 S = 15072 mm2 c.) Speed of vehicle = 18 km/h 1 km = 1000 m 1 hr = 60 x 60 = 3600 s 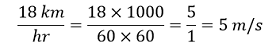
Distance travelled by the vehicle in 1 s = 5 m d.) Given relative density of lead = 11.3 We know that, 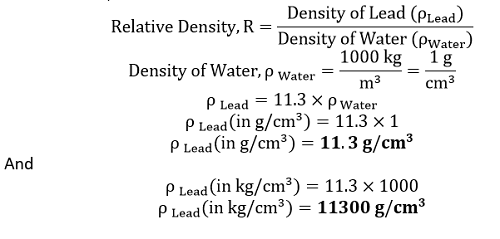
Question 2.2: Fill in the blanks by suitable conversion of units.
Answer: a.) We know that, 1 kg = 1000 g 1 m = 100 cm 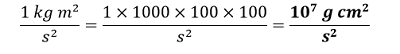
b.) We know that, 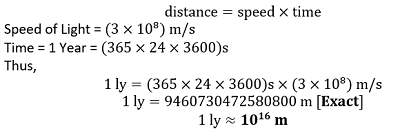
c.) We know that, 1 km = 1000 m 1 hr = 3600 s 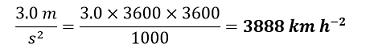
d.) Given that, G = 6.67 × 10-11 N m2 (kg)-2 N = kg m s-2 1 kg = 1000 g 1 m = 100 cm 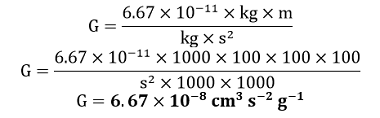
Question 2.3: A calorie is a unit of heat (energy in transit), which equals about 4.2 J, where 1J =1 kg m2 s. Suppose we employ a system of units in which the unit of mass equals α kg, the unit of length equals β m, and the unit of time is γ s. Show that a calorie has a magnitude of 4.2 α-1 β-2 γ2 in terms of the new units. Answer: 1 calorie = 4.2 J = 4.2 kg m2 s-2 
Question 2.4: Explain this statement clearly: "To call a dimensional quantity 'large' or 'small' is meaningless without specifying a standard for comparison". In view of this, reframe the following statements wherever necessary.
Answer: When compared to some other standard item of the same type, an object is said to be enormous or small. For instance, a ship is far larger than a bicycle in terms of size. The following comparison of their re framed phrase is:
Question 2.5: A new unit of length is chosen such that the speed of light in a vacuum is unity. What is the distance between the Sun and the Earth in terms of the new unit if light takes 8 min and 20 s to cover this distance? Answer: We wish to determine the distance between the Sun and the Earth, and we know that the speed of light in a vacuum is unity. We know that, 
Question 2.6: Which of the following is the most precise device for measuring length?
Answer: Option C is the correct answer. Device which has the minimum least count is said to be more precise device a.) Vernier Callipers It has 20 division on the sliding scale 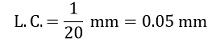
b.) Screw Gauge It has 100 division on the circular scale and a pitch of 1 mm 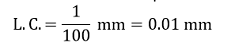
c.) Optical Instrument Within a wavelength of light Wavelength of light is ? 589 nm We can conclude that the optical instrument is the tool that measures length with the greatest degree of accuracy. Question 2.7: A student measures the thickness of a human hair by looking at it through a microscope of magnification 100. He makes 20 observations and finds that the average width of the hair in the field of view of the microscope is 3.5 mm. What is the estimate on the thickness of the hair? Answer: Given that 100 is the magnification, The hair in the microscope's field of view is typically 3.5 mm wide. Actual estimated hair thickness equals average field of vision width times 100 times magnification, or 3.5 mm/0.035 mm. Estimated hair thickness is 0.035 mm is the answer Question 2.8: Answer the following :
Answer: a.) The thread should first be wound around a cylindrical coil with its turns touching one another side by side as you go. Once the thread has been completely wrapped around the coil, measure the length of the coil up to the wrapped area. Let l represent the coil's length up to the wrapped segment and n represent the number of twists the coil has received. The thread's diameter can be calculated using, d = length of coiled coil multiplied by number of turns, or l × n b.) Given that there are 200 divisions on the circular scale, the screw gauge's pitch is 1.0 mm. An instrument is more exact when it has minimum least count value. The screw gauge's least count is specified as, Least count= pitch Number of division The value of least count falls as the number of divisions rises, according to the relationship mentioned above. As a result, the screw gauge's accuracy improves. However, the number of divisions can only go up to a certain point until it becomes challenging to add more divisions to the circular scale. By increasing the number of divisions on the circular scale, it is therefore feasible to arbitrarily enhance the screw gauge's accuracy. c.) Reliable describes the level of measuring precision. As the number of measurements rises, reliability does as well. It's because the likelihood of random error in a big number of measurements is far lower than the likelihood of random error in a small number of observations. The set of 100 diameter measurements is therefore more trustworthy than the set of 5 measurements. Question 2.9: The photograph of a house occupies an area of 1.75 cm2 on a 35 mm slide. The slide is projected onto a screen, and the area of the house on the screen is 1.55 m2. What is the linear magnification of the projector-screen arrangement? Answer: Given that, Area of house on the slide is = 1.75 cm2 Area of the image of house which formed on the screen is = 1.55 cm2 We know that 1 m = 100 cm = 102 cm Thus, Area of the image of house which formed on the screen is = 1.55 cm2 × 104 cm2 Arial Magnification, 
Question 2.10: State the number of significant figures in the following:
Answer: A number's significant figures are the digits that add to its measurement resolution by having significance. All digits are included in this, with the exception of: 1.) All leading zeros 2.) Trailing zeros when they are merely placeholders to indicate the scale of the number (exact rules are explained at identifying significant figures) 3.) False digits introduced, for instance, by calculations performed with a higher level of precision than the original data or measurements reported with a higher level of precision than the equipment supports. a.) 0.007 = 7 × 10-3 Significant digit is 7. Thus only 1 significant digit. b.) Number of significant digit is 3 c.) Every non-zero number has significance. Any zeros that come before a non-zero number are meaningless. Every zero that appears both at the end of the number and immediately to the right of the decimal point is significant. The zero that comes before the decimal point is the sole unimportant digit in this number. Consequently, there are 4 significant digits. d.) Every non-zero number has significance. Every zero that appears both at the end of the number and immediately to the right of the decimal point is significant. Consequently, there are 4 significant digits. e.) All the digits are significant (no leading and trailing zero). No. of significant digits = 4 f.) Significant digits: 6032 Number of significant digits = 4 Question 2.11: The length, breadth and thickness of a rectangular sheet of metal are 4.234 m, 1.005 m, and 2.01 cm, respectively. Give the area and volume of the sheet to correct significant figures. Answer: A = 2 × (L × B + B × T + T × L) ∴A = 2 × (4.234 × 1.005 + 1.005 × 0.0201 + 0.0201 × 4.234) ∴A = 2 × (4.2552 + 0.0202 + 0.0851) ∴A = 8.721 m2 ∴A = 8.721 m2 to correct significant digits V = L × B × T ∴V = 4.234 × 1.005 × 0.0201 ∴V = 0.0855 m3 to correct significant digits Question 2.12: The mass of a box measured by a grocer's balance is 2.30 kg. Two gold pieces of masses 20.15 g and 20.17 g are added to the box. What is
Answer: mi = 2.300 kg (two significant digits) m1 = 20.15 g (four significant digits) m2 = 20.175 g (four significant digits) a.) Adding, 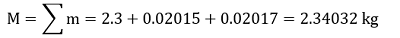
The final mass should have no more than 2 significant digits, though, because the beginning mass has at least 2 significant digits. Therefore M = 2.3 kg b.) Subtracting m2 - m1 = 0.02 g Since the original mass has four significant digits, the outcome can also have four or less. So, in this case, there are two significant digits. Question 2.13: A physical quantity P is related to four observables a, b, c and d as follows: 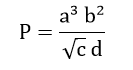
The percentage errors of measurement in a, b, c and d are 1%, 3%, 4% and 2%, respectively. What is the percentage error in the quantity P? If the value of P calculated using the above relation turns out to be 3.763, to what value should you round off the result? Answer: Given that, 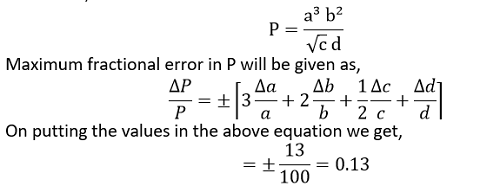
Percentage error in P is 13% Value of P is given as 3.763 By rounding the value up to two correct decimal place we get the answer as 3.8. Question 2.14: A book with many printing errors contains four different formulas for the displacement y of a particle undergoing a certain periodic motion: 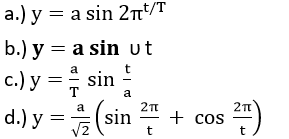
(a = maximum displacement of the particle, v = speed of the particle, T = time-period of motion). Rule out the wrong formulas on dimensional grounds. Answer: Since the displacements of the particle are the subject of all equations, length should be a dimension in all of them. Now, verify that all displacement equations are dimensionally accurate. 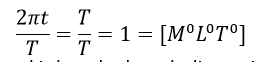
Here, a is the amplitude and it has the length dimension. The equation is accurate, thus. b.)We know that vt should be dimensionless since the trigonometric functions are also dimensionless. vt = (LT-1)(T) = L = [M0L1T0] The given equation is therefore incorrect. 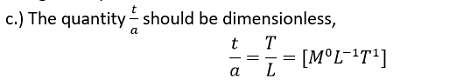
As a result, it is dimensionally inaccurate as well. 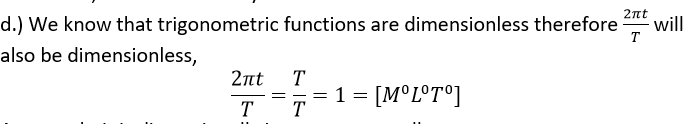
As a result, it is dimensionally inaccurate as well. Question 2.15: A famous relation in physics relates 'moving mass' m to the 'rest mass' mo of a particle in terms of its speed v and the speed of light, c (This relation first arose as a consequence of special relativity due to Albert Einstein). A boy recalls the relation almost correctly but forgets where to put the constant c. He writes :> 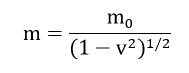
Guess where to put the missing c. Answer: 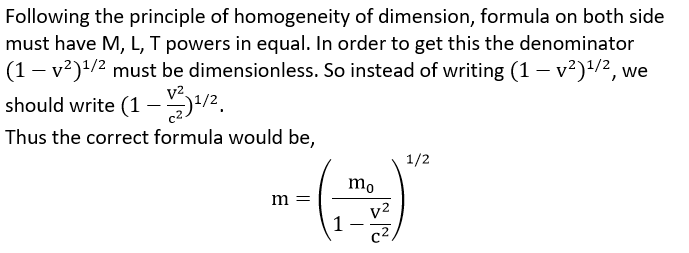
Question 2.16: The unit of length convenient on the atomic scale is known as an angstrom and is denoted by Å: 1 Å = 10-10 m. The size of a hydrogen atom is about 0.5 Å. What is the total atomic volume in m3 of a mole of hydrogen atoms? Answer: Given that, 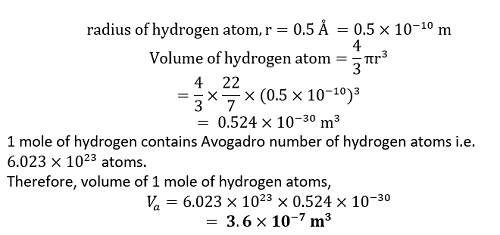
Question 2.17: One mole of an ideal gas at standard temperature and pressure occupies 22.4 L (molar volume). What is the ratio of molar volume to the atomic volume of a mole of hydrogen (Take the size of the hydrogen molecule to be about 1 Å)? Why is this ratio so large? Answer: Given that, 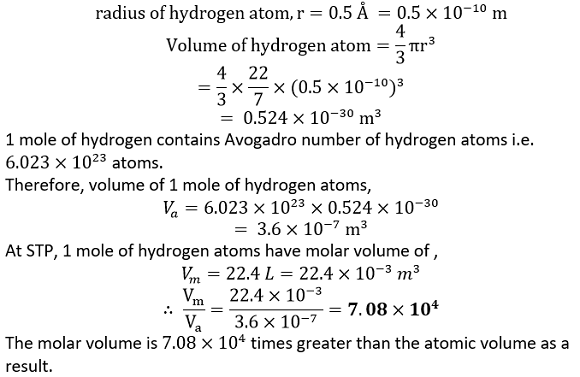
Because of the high inter-atomic separation in hydrogen gas, the ratio is very high. Question 2.18: Explain this common observation clearly: If you look out of the window of a fast-moving train, the nearby trees, houses etc., seem to move rapidly in a direction opposite to the train's motion, but the distant objects (hilltops, the Moon, the stars etc.) seem to be stationary (In fact, since you are aware that you are moving, these distant objects seem to move with you). Answer: Line of sight is referred to as the hypothetical path connecting an object and the observer's eye. The line of sight changes drastically as a train is going, which causes nearby stationary things, such houses, trees, and other structures, to appear to be moving quickly in the opposite direction. However, due to their great distance, distant things like trees, stars, and other celestial bodies appear to be immobile. As a result, the line of sight does not quickly alter its course. Question 2.19: The principle of 'parallax' in section 2.3.1 is used in the determination of distances of very distant stars. The baseline AB is the line joining the Earth's two locations six months apart in its orbit around the Sun. That is, the baseline is about the diameter of the Earth's orbit ? 3 × 1011m. However, even the nearest stars are so distant that with such a long baseline, they show parallax only of the order of 1" (second of arc) or so. A parsec is a convenient unit of length on the astronomical scale. It is the distance of an object that will show a parallax of 1" (second of arc) from opposite ends of a baseline equal to the distance from the Earth to the Sun. How much is a parsec in terms of metres? Answer: Diameter of Earth's orbit = 3 × 1011 m Radius of Earth's orbit r = 1.5 × 1011 m Let the distance parallax angle be θ = 1″ (s) = 4.847 × 10-6 rad. Let the distance of the star be D. Parsec is defined as the distance at which the average radius of the Earth's orbit subtends an angle of 1″ Therefore, 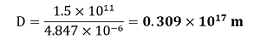
Hence 1 parsec ? 3.09 × 1016 m. Question 2.20: The nearest star to our solar system is 4.29 light-years away. How much is this distance in terms of parsecs? How much parallax would this star (named Alpha Centauri) show when viewed from two locations of the Earth six months apart in its orbit around the Sun? Answer: The distance travelled by the light in a year is known as a light year. Thus, Speed of Light = (3× 108) m/s Time = 1 Year = (365 × 24 × 3600)s Thus, 
Question 2.21: Precise measurements of physical quantities are a need for science. For example, to ascertain the speed of an aircraft, one must have an accurate method to find its positions at closely separated instants of time. This was the actual motivation behind the discovery of radar in World War II. Think of different examples in modern science where precise measurements of length, time, mass etc., are needed. Also, wherever you can, give a quantitative idea of the precision needed. Answer: Science must utilize accurate instruments to take precise measurements. Precision in measurement is required for several operations. A precise device is used in the radiography technique to measure the space between individual atoms. For instance, the precise moment when a neutron collides with a radioactive neutron occurs during a nuclear reaction. It is possible to determine the time for several chemical reactions using ultra-short laser pulses. Question 2.22: Just as precise measurements are necessary in science, it is equally important to be able to make rough estimates of quantities using rudimentary ideas and common observations. Think of ways by which you can estimate the following (where an estimate is difficult to obtain, try to get an upper bound on the quantity) :
Answer: a.) Let us assume that during the monsoon season the average rainfall recorded by Meteorologist in India was, 100 cm. h=100 cm = 1m Area of India = A=3.3× 1012 m2 Density of Water = 1000 kg/m3 . Mass of rain bearing cloud m=ρAh m=mass of rain bearing cloud ρ = density of water A= area of India h=average rainfall recorded Substituting values we get, m = 1000 × 3.3 × 1012 ×1 = 3.3 × 1015kg Therefore, mass of rain bearing cloud is 3.3× 115kg. b.) Let us first consider an empty boat floating in water. So in this case there would be some kind of water displacement by the empty boat. In that case the volume of water displaced by the empty boat will be written as V1=Ad1 V1= Volume of water displaced by the empty boat. A= Base area of the boat. d1= depth of boat submerged in water. Now move the elephant in the empty boat and then measure the new depth of boat in water. The volume of water displaced by boat while carrying the elephant will be given as V2=Ad2 V2= Volume of water displaced by the boat while carrying the elephant. d1= depth of boat submerged in water when loaded with elephant. Now the volume of water displaced by elephant is V = V2 - V1 = Ad2 - Ad1 = A(d2 - d1) Mass of the elephant m=ρV = ρA(d2 - d1) c.) The wind speed during a storm can be estimated by using a gas-filled balloon. The gas must be lighter than air, so that balloon floats in air. The figure below shows the required apparatus to measure the speed of wind during wind storm. 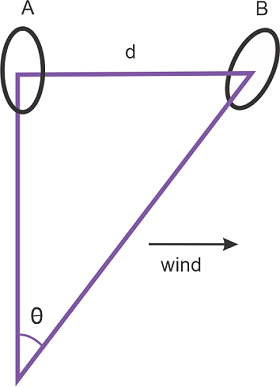
The position A of the balloon is the position when there is no wind and position B of the balloon is the position when the wind is blowing and displacing the balloon from its original position. By knowing the value of d, the speed of the wind storm can be calculated. The speed of wind can also be calculated by using an anemometer. The blowing wind rotates the anemometer and the rotation of anemometer in one minute gives the information about the wind speed during the wind storm. d.) Radius of human head = 8 × 10-2m Thickness of human hair = 5 × 10-5m Number of hair strands of hair, n = AHah =π R2 πt2 = (Rt)2 n=number of hair strands R=radius of head t=thickness of hair Substituting values, n =(8× 10-2 × 5 × 10-5)2 = 2.56× 106 e.) For example let us take a classroom of length of 10m and let its width be 8m and the height of the classroom be 4m. Volume V of the classroom will be, V = lbh V = volume of the classroom. l = length of the classroom. b = width of the classroom. h = height of the classroom. Substituting values we get, V = 10 × 8 × 4 = 320m3 So, 22.4× 10-3 m3 of air have 6.02× 1023 molecules of air. So number of molecules present in classroom, n = 6.02 × 1023× 22.4 × 10-3 × V Substituting values we get, n = 6.02 × 1023 × 22.4 × 10-3 × 320 = 8.6× 1027 Question 2.23: The Sun is a hot plasma (ionized matter) with its inner core at a temperature exceeding 107 K, and its outer surface at a temperature of about 6000 K. At these high temperatures, no substance remains in a solid or liquid phase. In what range do you expect the mass density of the Sun to be, in the range of densities of solids and liquids or gases? Check if your guess is correct from the following data: a mass of the Sun = 2.0 × 1030 kg, the radius of the Sun = 7.0 × 108 m. Answer: Mass = 2 x 1030 kg Radius = 7 x 108 m 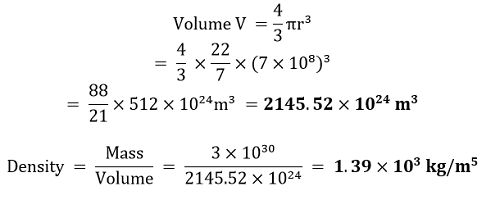
The density is between that of liquids and solids. Due to the sun's inner layer's strong gravitational pull on the outer layer, it is dense. Question 2.24: When the planet Jupiter is at a distance of 824.7 million kilometers from the Earth, its angular diameter is measured to be 35.72" of arc. Calculate the diameter of Jupiter. Answer: Distance between Jupiter and Earth, D= 824.7 million kilometers = 824.7 x 106 km Angular diameter θ = 35.72" = 35.72 x 4.85 x 10-6 rad Diameter of Jupiter, d = θ x D = 173.241 x 10-6 x 824.7 x 106 km =142871 = 1.43 x 105 km Additional ExerciseQuestion 2.25: A man walking briskly in the rain with speed v must slant his umbrella forward, making an angle θ with the vertical. A student derives the following relation between θ and v: tan θ = v and checks that the relation has a correct limit: as v →0, θ →0, as expected (We are assuming there is no strong wind and that the rain falls vertically for a stationary man). Do you think this relation can be correct? If not, guess the correct relation. Answer: Following the principle of homogeneity of dimensional equations, The relation given here is v = tan θ. Since tan θ is a trigonometric function, so basically that's dimensionless. Also the dimension of v is [L1 T-1]. So we can say that the given relation is not correct. If we divide the L.H.S. by the velocity of the rain u, then we can make the relation correct. On doing so the relation becomes 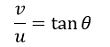
This equation is dimensionally correct. Question 2.26: It is claimed that two caesium clocks, if allowed to run for 100 years, free from any disturbance, may differ by only about 0.02 s. What does this imply for the accuracy of the standard caesium clock in measuring a time interval of 1 s? Answer Total time = 100 years = 100 x 365 x 24 x 60 x 60 s Error in 100 years = 0.02 s 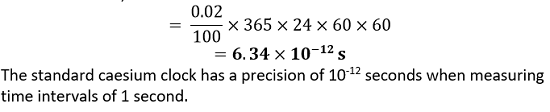
Question 2.27: Estimate the average mass density of a sodium atom, assuming its size to be about 2.5 Å (Use the known values of Avogadro's number and the atomic mass of sodium). Compare it with the mass density of sodium in its crystalline phase: 970 kg m-3. Are the two densities of the same order of magnitude? If so, why? Answer: diameter of sodium= 2.5 A = 2.5 x 10-10 m Therefore, radius is 1.25 x 10-10m The volume of a sodium atom, 
In solid state sodium has density of about 4669.2 kg m-3, while in crystalline form its density is 970 kg m-3. Therefore these are in different order. In solid forms atoms are more tightly packed while in the crystalline form atoms forms a sequence which sometimes forms a void or is empty. Because of this density in solid is more when compared to crystalline phase. Question 2.28: The unit of length convenient on the nuclear scale is a fermi: 1 f = 10-15 m. Nuclear sizes obey roughly the following empirical relation : r = r0A1/3 where r is the radius of the nucleus, A its mass number, and r0 is a constant equal to about 1.2 f. Show that the rule implies that nuclear mass density is nearly constant for different nuclei. Estimate the mass density of the sodium nucleus. Compare it with the average mass density of a sodium atom obtained in Exercise. 2.27. Answer: The radius of the nucleus 
The nuclear mass density is therefore substantially greater than the atomic mass density for the sodium atom we obtained in exercise 2.27. Question 2.29: A LASER is a source of very intense, monochromatic, and unidirectional beam of light. These properties of laser light can be exploited to measure long distances. The distance of the Moon from the Earth has already been determined very precisely using a laser as a source of light. A laser light beamed at the Moon takes 2.56 s to return after reflection at the Moon's surface. How much is the radius of the lunar orbit around the Earth? Answer: The amount of time needed for the laser beam to re-enter Earth after being reflected by the Moon's surface = 2.56 s The speed of laser light is c = 3 x 108 m/s. Let d be the distance of the Moon from the Earth, The time taken by laser signal to reach the Moon, 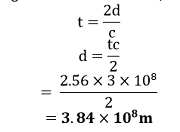
Question 2.30: A SONAR (sound navigation and ranging) uses ultrasonic waves to detect and locate objects underwater. In a submarine equipped with a SONAR, the time delay between the generation of a probe wave and the reception of its echo after reflection from an enemy submarine is found to be 77.0 s. What is the distance of the enemy submarine? (Speed of sound in water = 1450 m/s). Answer: Speed of sound in water,v = 1450 m s-1 The time interval from when an echo is generated until it is received after reflection, 2t= 77.0 s Time taken by the sound waves to reach the submarine, 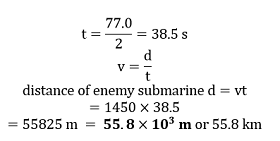
Question 2.31: The farthest objects in our Universe discovered by modern astronomers are so distant that light emitted by them takes billions of years to reach the Earth. These objects (known as quasars) have many puzzling features which have not yet been satisfactorily explained. What is the distance in km of a quasar from which light takes 3.0 billion years to reach us? Answer: The amount of time it takes for quasar light to reach the observer, t = 3.0 billion years = 3.0 x 109 years = 3.0 x 109 x 365 x 24 x 60 x 60 s = 94608000 x 109 s = 9.46 x 1016 m Speed of light = 3 x 108 m/s Distance of quasar from Earth = 3.0 x 108 x 9.46 x 1016 m = 28.38 x 1024 m Question 2.32: It is a well-known fact that during a total solar eclipse-the disk of the moon almost completely covers the disk of the Sun. From this fact and the information you can gather from examples 2.3 and 2.4, determine the approximate diameter of the moon. Answer: From examples 2.3 and 2.4, we get the following data Distance between Moon and Earth = 3.84 x 108 m Distance between Sun and Earth = 1.496 x 1011 m Diameter of sun = 1.39 x 109 m Angular diameter of sun,θ = 1920″ = 1920 x 4.85 x 10-6 rad = 9.31 x 10-3 rad [1″ = 4.85 x 10-6 rad] The sun and moon must have similar angular diameters because, during a total solar eclipse, the moon's disc fully obscures the sun's disc. Angular diameter of moon, θ = 9.31 x 10-3 rad The earth-moon distance, S = 3.8452 x 108 m Therefore, the diameter of the moon, D = θ × S = 9.31× 10-3 × 3.8452 × 108 m = 35.796 × 105 m
Next TopicClass 11 Physics Chapter 3
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









