NCERT Solutions Class 6 MathsChapter 4: Basic Geometrical IdeasExercise 4.11. Use the figure to name: 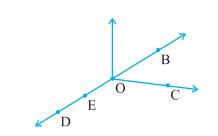
(a) Five points Answer: O, B, C, D, E Explanation: Points are the dots that determines a location. (b) A line Answer: DE, DO, DB, ED, EB Explanation: A line is formed by joining two points. There are multiple lines in the above diagram. For example, OB, OE, OD, OC DE, DO, DB EO, ED, EB (c) Four rays Answer: ED, EB, DB, DE Explanation: A ray is a type of line that goes endlessly in a single direction. There are multiple rays in the above diagram. OB, OE, OD, OC DE, DO, DB EO, ED, EB (d) Five line segments Answer: ED, EB, DB, DE, OC Explanation: There are multiple line segments in the above diagram. OB, OE, OD, OC DE, DO, DB EO, ED, EB 2. Name the line given in all possible (twelve) ways, choosing only two letters at time from the four given. 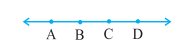
Answer:
3. Use the figure to name: 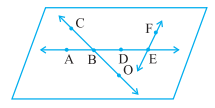
(a) Line containing point E. Answer: AE Explanation: There are multiple lines containing point E. For example, AE, BE, DE, FE (b) Line passing through A. Answer: AE Explanation: There are multiple lines passing through A. For example, AE, AD, and AB (c) Line on which O lies Answer: OC or CO Explanation: O lies on the line OC, also known as CO. (d) Two pairs of intersecting lines. Answer: Pair 1: CO and AE Pair 2: AE and EF Explanation: A pair of intersecting line has only one point in common. There are multiple names of two pairs of these intersecting lines. For example, 1. OC and EA EA and FE 2. OC and AB EF and DE 3. OC and AD FE and EB 4. How many lines can pass through (a) one given point? Answer: Infinite / Countless Explanation: Infinite number of lines can pass through one point. (b) two given points? Answer: 1 Explanation: Only one line can pass through two given points. 5. Draw a rough figure and label suitably in each of the following cases: (a) Point P lies on AB. Diagram: 
(b) XY and PQ intersect at M. Diagram: 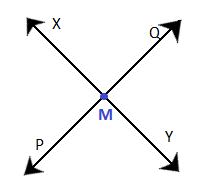
(c) Line l contains E and F but not D. Diagram: 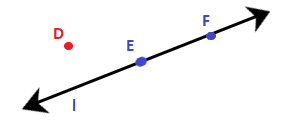
(d) OP and OQ meet at O. Diagram: 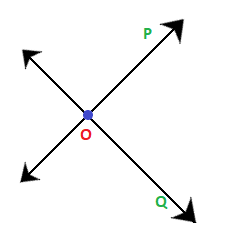
6. Consider the following figure of line MN. Say whether following statements are true or false in context of the given figure. 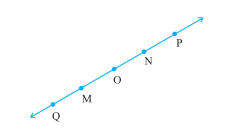
(a) Q, M, O, N, P are points on the line MN. Answer: True Explanation: Q, M, O, N, P are the points on the line MN. Q and P also lies on the line MN, (b) M, O, N are points on a line segment MN . Answer: True Explanation: Q, M, O, N, P are the points on the line segment MN. (c) M and N are end points of line segment MN . Answer: True Explanation: A line segment is formed between the two end points. It is named according to the two end-points. Thus, the line MN has two end points M and N. (d) O and N are end points of line segment OP . Answer: False Explanation: A line segment is formed between the two end points. It is named according to the two end-points. Thus, the line OP has two endpoints O and P. (e) M is one of the end points of line segment QO. Answer: False Explanation: The line QO has two endpoints O and Q. M is only the point on the line QO, not an endpoint. (f) M is point on ray OP. Answer: False Explanation: A ray is a line in a single direction. The ray OP does not contains the point O because both has opposite directions. (g) Ray OP is different from ray QP. Answer: True Explanation: Ray OP contain points O,P, and N, while ray QP contain points Q, M, O, N, P. (h) Ray OP is same as ray OM. Answer: False Explanation: Ray OP contain points O,P, and N, while ray OM contain points O and M. (i) Ray OM is not opposite to ray OP. Answer: False Explanation: Ray OM is opposite to ray OP becuase both has opposite directions. (j) O is not an initial point of OP. Answer: False Explanation: A ray starts from an initial point. Thus, O is an intial point of ray OP. (k) N is the initial point of NP and NM. Answer: True Explanation: A ray starts from an initial point. Thus, N is the initial point of both the rays NP and NM. Exercise 4.21. Classify the following curves as (i) Open or (ii) Closed. 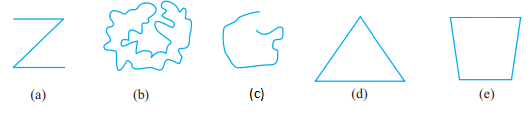
(a) Open curve (b) Closed curve (c) Open curve (d) Closed curve (e) Closed curve Explanation: Open curves are the curves that are joined end to end. It means the end points of the curve are joined together. Closed curves are the curves that have open ends. It means the end points of the curve are different. 2. Draw rough diagrams to illustrate the following: (a) Open curve Diagram: 
(b) Closed curve. Diagram: 
We can draw any type of open or closed curve. 3. Draw any polygon and shade its interior. A polygon is a figure made of three or more line segments. There are different types of polygons. Diagram: 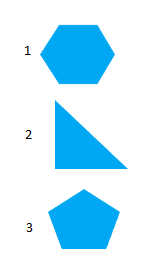
Explanation:
4. onsider the given figure and answer the questions: 
(a) Is it a curve? Answer: Yes It is a curve because a curve has line segments linked end to end. (b) Is it closed? Answer: It is a closed figure because the end points of the above figure are joined end to end. 5. Illustrate, if possible, each one of the following with a rough diagram: (a) A closed curve that is not a polygon. Diagram: 
Explanation: (b) An open curve made up entirely of line segments. Diagram: 
Explanation: A curve has line segments linked end to end. A polygon is a closed figure made of three or more line segments. A curve can be made of different types of curves and line segments, while a polygon is only made of line segments. (c) A polygon with two sides. Diagram: Not possible. We cannot make a closed figure made of two line segments. Explanation: A polygon is a closed figure made of three or more line segments. Exercise 4.31. Name the angles in the given figure. 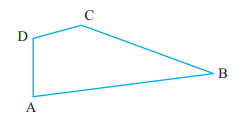
Answer: ∠ADC or ∠D or ∠CDA ∠DCB or ∠C or ∠BCD ∠CBA or ∠B or ∠ABC ∠BAD or ∠A or ∠DAB 2. In the given diagram, name the point(s), 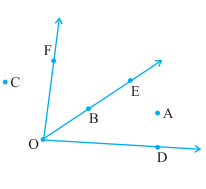
(a) In the interior of ∠DOE Answer: point A Explanation: Point A is the only point lying in the interior (inside) of the ∠DOE. (b) In the exterior of ∠EOF Answer: A, C, D Explanation: Point A, C, and D lies on the exterior (outside) of ∠EOF. (c) On ∠EOF Answer: E, B, O, F Explanation: Point E, B, O, and F lies on the boundary of the angle ∠EOF. 3. Draw rough diagrams of two angles such that they have (a) One point in common. Diagram: 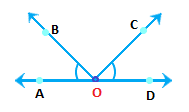
Two angles: ∠AOB and ∠DOC Common point: O (b) Two points in common. Diagram: 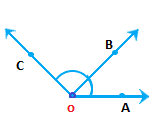
Two angles: ∠AOB and ∠BOC Common point: O, B (c) Three points in common. Diagram: 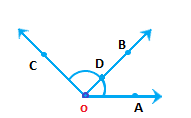
Two angles: ∠AOB and ∠BOC Common point: O, B, D (d) Four points in common. Diagram: 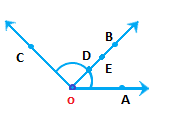
Two angles: ∠AOB and ∠BOC Common point: O, B, D, E (e) One ray in common. Diagram: Two angles: ∠AOB and ∠BOC Common ray: OB 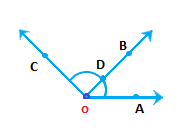
Exercise 4.41. Draw a rough sketch of a triangle ABC. Mark a point P in its interior and a point Q in its exterior. Is the point A in its exterior or in its interior? Diagram: 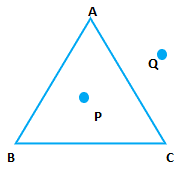
A lies neither on the exterior nor interior. Explanation: Point A is present on the boundary of the triangle. Hence, it is neither present in the exterior nor interior of the triangle. 2. (a) Identify three triangles in the figure. 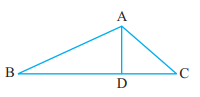
Answer: ?ABC, ?ADC, ?ABD (b) Write the names of seven angles. Answer: ∠BAC, ∠ADB, ∠CAD, ∠BAD, ∠B, ∠C, ∠ADC ∠ABD or ∠DBA or ∠B ∠BDA or ∠ADB ∠ADC or ∠CDA ∠DCA or ∠ACD or ∠C ∠CAD or ∠DAC ∠DAB or ∠BAD ∠CAB or ∠BAC or ∠A (c) Write the names of six line segments. Answer: AB, BD, DC, AC, AD, BC AB or BA BD or DB DC or CD AC or CA AD or DA BC or CB Note: The names of the angles, line segments, and traingle can be both clockwise or anti-clockwise. We can select any option.(d) Which two triangles have ∠B as common? Answer: ?ABC, ?ABD Exercise 4.51. Draw a rough sketch of a quadrilateral PQRS. Draw its diagonals. Name them. Is the meeting point of the diagonals in the interior or exterior of the quadrilateral? Diagram: 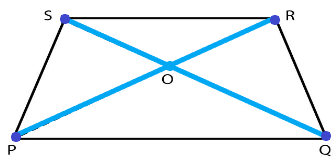
Diagonals: PR, SQ Meeting point of diagonals: O The meeting point of the quadrilateral lies in the interior of the traingle. Explanation: Diagonals are always present in the interior of the quadrilateral. Hence, the meeting point or the intersecting point of the quadrilateral also lies in its interior. 2. Draw a rough sketch of a quadrilateral KLMN. Diagram: 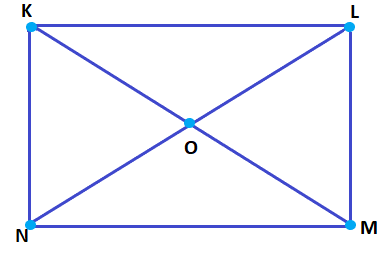
State, (a) two pairs of opposite sides Answer: KL and NM KN and ML (b) two pairs of opposite angles Answer: ∠K and ∠M ∠L and ∠N (c) two pairs of adjacent sides Answer: NM and LM LK and KN Or MN and NK KL and NM (d) two pairs of adjacent angles Answer: ∠K and ∠L ∠M and ∠N Or ∠K and ∠N ∠M and ∠L Exercise 4.61. From the figure, identify : 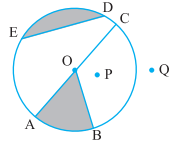
(a) the centre of circle Answer: O O is the center point of the circle. (b) three radii Answer: OC, OA, OB OC, OA, and OB are three radii of the circle. Radius = Diameter/2 (c) a diameter Answer: AC A diameter always pass through the center of the circle touching the two points on the circumference. Hence, AC is the only diameter in the above figure. (d) a chord Answer: ED A chord is a line segment touching the two points on the circumference. (e) two points in the interior Answer: O, P O and P are the two points lying inside the circle. (f) a point in the exterior Answer: Q Q is the point lying outside the circle. (g) a sector Answer: OAB AOB or OAB or OBA AOB is the sector of the above circle. It is represented by the shaded portion. (h) a segment Answer: ED ED is the segment of the above circle. It is also represented by the shaded portion. 2. (a) Is every diameter of a circle also a chord? Answer: Yes Explanation: A chord on a circle is formed by joining any two points on its circumference or boundary. A chord can also pass through the center of the circle. Hence, every diameter of a circle also a chord. (b) Is every chord of a circle also a diameter? Answer: A chord on a circle is formed by joining any two points on its circumference or boundary. A diameter also pass through the center of the circle, while a chord can/cannot pass through the center. Hence, every chord of a circle is not always the diameter. 3. Draw any circle and mark 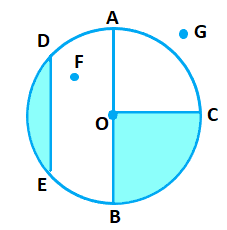
(a) its centre O is the center of the circle. (b) a radius OB is the radius of the circle. (c) a diameter AB is the diameter of the circle. (d) a sector BOC is the sector of the circle. (e) a segment DE is the segment of the circle. (f) a point in its interior F is the point in the interior of the circle. (g) a point in its exterior G is the point in the exterior of the circle. (h) an arc BC is the arc of the circle. 4. Say true or false : (a) Two diameters of a circle will necessarily intersect. Answer: True Explanation: Every diameter of the circle passes through the center point of the circle. Hence, two diameters of a circle will necessarily intersect. (b) The centre of a circle is always in its interior. Answer: True Explanation: Center means the mid point of a circle lying inside its boundary. Hence, the centre of a circle is always in its interior.
Next TopicClass 6 Maths Chapter 5
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share









