What is the 2s complement in C?

The 2s complement in C is generated from the 1s complement in C. As we know that the 1s complement of a binary number is created by transforming bit 1 to 0 and 0 to 1; the 2s complement of a binary number is generated by adding one to the 1s complement of a binary number.

In short, we can say that the 2s complement in C is defined as the sum of the one's complement in C and one.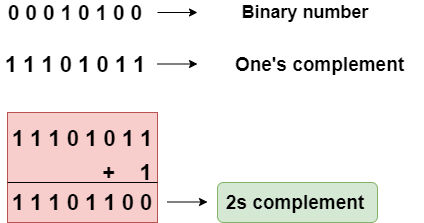

In the above figure, the binary number is equal to 00010100, and its one's complement is calculated by transforming the bit 1 to 0 and 0 to 1 vice versa. Therefore, one's complement becomes 11101011. After calculating one's complement, we calculate the two's complement by adding 1 to the one's complement, and its result is 11101100.

Let's create a program of 2s complement.

Output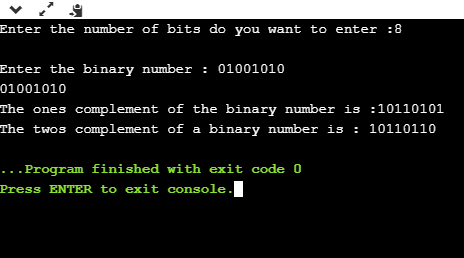

Analysis of the above program,

• First, we input the number of bits, and it gets stored in the 'n' variable.
• After entering the number of bits, we declare character array, i.e., char binary[n+1], which holds the binary number. The 'n' is the number of bits which we entered in the previous step; it basically defines the size of the array.
• We declare two more arrays, i.e., onescomplement[n+1], and twoscomplement[n+1]. The onescomplement[n+1] array holds the ones complement of a binary number while the twoscomplement[n+1] array holds the two's complement of a binary number.
• Initialize the carry variable and assign 1 value to this variable.
• After declarations, we input the binary number.
• Now, we simply calculate the one's complement of a binary number. To do this, we create a loop that iterates throughout the binary array, for(int i=0;i<n;i++). In for loop, the condition is checked whether the bit is 1 or 0. If the bit is 1 then onescomplement[i]=0 else onescomplement[i]=1. In this way, one's complement of a binary number is generated.
• After calculating one's complement, we generate the 2s complement of a binary number. To do this, we create a loop that iterates from the last element to the starting element. In for loop, we have three conditions:
  • If the bit of onescomplement[i] is 1 and the value of carry is 1 then we put 0 in twocomplement[i].
  • If the bit of onescomplement[i] is 0 and the value of carry is 1 then we put 1 in twoscomplement[i] and 0 in carry.
  • If the above two conditions are false, then onescomplement[i] is equal to twoscomplement[i].

Signed integers are frequently represented in C using the two's complement notation. Using the same binary representation offers a mechanism to express both positive and negative integers. The most significant bit (MSB) is used as the sign bit in a two's complement representation, where 0 denotes a positive integer, and 1 denotes a negative number.

Starting with a negative number's absolute value in binary form, you may take the one's complement (bitwise negation) of that value to get the two's complement representation of the negative integer. You add 1 to the resultant value to acquire the representation of the two's complement.

The two's complement encoding in C can represent signed integers and can perform fast arithmetic operations. One benefit of employing two's complement is the ability to do addition and subtraction using the same binary operations as for unsigned numbers.

The binary numbers are added together like unsigned integers when adding two's complement. A carry-out from the location of the main critical bit is just disregarded. Due to this fact, handling signed numbers differently is not necessary, and addition becomes simple.

Consider adding -5 and -3 using the 8-bit two's complement representation, for instance:

Binary number for -5 is 11111011.

Binary number for -3 is 11111101.

carrying out the addition:

The answer is 111110100, which in two's complement is equal to -8.

Similar to addition, subtraction may be done by treating the second operand's two's complement as if it were addition. In other words, you add the two's complement of a negative number to the first operand to remove it.

For instance, when -3 is subtracted from -5:

In binary, -5 is represented by 11111011 and -(-3) by 00000011 (two's complement of -3)

Carrying out the subtraction

The outcome is 11111110, which in two's complement is equal to -8.

Conclusion:

In C, the 2s complement is a binary representation of a negative number that is created by adding one to the 1s complement. Computer systems frequently employ this idea to represent signed numbers and efficiently carry out arithmetic operations.

To get the 2s complement of a binary integer, one must first determine the 1s complement of the number by flipping the bits. After that, the representation of the 2s complement is obtained by adding one to the 1s complement. The most significant bit (MSB) will function as a sign bit by expressing whether a number is positive or negative.

The computation of the 2s complement for a given binary integer is shown in the attached C program. The user is prompted to input both the binary number and the number of bits. After that, the program does the required procedures to acquire the 1s complement, and then the 2s complement. The findings are then shown.

In computer science and programming, it's crucial to comprehend the 2s complement representation since it makes it possible to handle negative values expressed in binary effectively. It makes addition, subtraction, and logical operations simpler on both positive and negative numbers. The range of representable integers is symmetric about zero due to the 2s complement representation, making it appropriate for various numerical operations.

Programmers may conduct arithmetic operations, work with binary data, and design algorithms using signed integers in C and other programming languages by understanding the idea of 2s complement and properly utilizing it.