C Program to find the roots of quadratic equationQuadratic equations are the polynomial equation with degree 2. It is represented as ax2 + bx +c = 0, where a, b and c are the coefficient variable of the equation. The universal rule of quadratic equation defines that the value of 'a' cannot be zero, and the value of x is used to find the roots of the quadratic equation (a, b). A quadratic equation's roots are defined in three ways: real and distinct, real and equal, and real and imaginary. 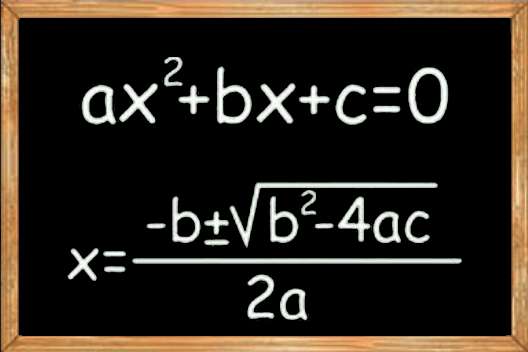
Nature of the rootsThe nature of the roots depends on the Discriminant (D) where D is.
Steps to find the square roots of the quadratic equation
Pseudo Code of the Quadratic Equation
Let's implements the above steps in a C program to find the roots of the quadratic equation. Output: 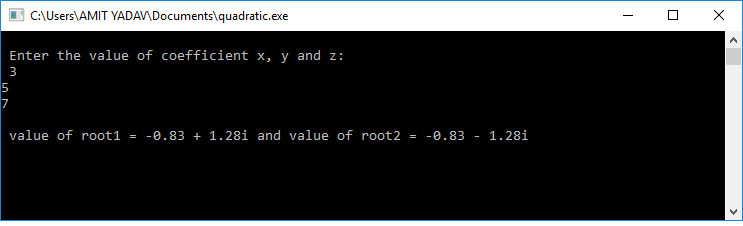
Let's create another C program in which we have used function. Output: 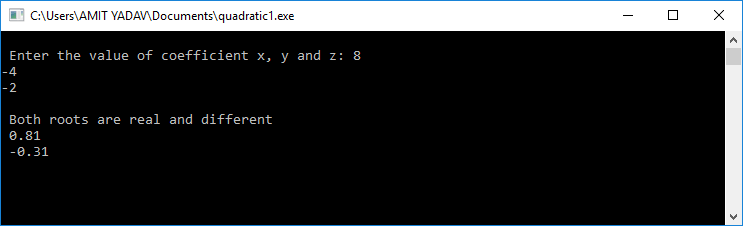
Next TopicType Casting vs Type Conversion
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










