Tail Recursion in CTail recursion in computer programming refers to a specific form of recursion where a function calls itself as its last step before producing an output. In simpler terms, in a tail-recursive function, the act of calling itself is the very last thing the function does before giving an output. This particular pattern allows specific programming languages and compilers to manage memory more effectively. They can reuse the current function's working space for the upcoming recursive call, which reduces the need for creating new segments of memory, leading to better efficiency in how the program runs. It's like when you're stacking up books. Let's say you have a pile of books and want to count how many there are. To do this, you count one book at a time and keep track of the total. When you're counting the last book, instead of finishing and saying the total out loud, you start counting the pile all over again with just one more book added to your total. This way, you're not really done with the counting until you've counted all the books, including the new one you just added. That's what we call "tail recursion". It's like starting a new round of counting from the beginning, but with some extra information you've collected. Uses of Tail Recursion:Tail recursion is mostly used in several calculations. Some of them are as follows: Calculating Factorials: As mentioned earlier, calculating the factorial of a number using tail recursion is a common example. The function keeps multiplying the number with an accumulator as it goes through each recursive call. Calculating Exponentiation: Another example is computing the power of a number using tail recursion. The function recursively multiplies the base by itself, reducing the exponent each time until it becomes zero. Finding Fibonacci Numbers: Finding Fibonacci numbers using tail recursion is possible. The function calculates the sum of the last two Fibonacci numbers and passes them as arguments in the recursive call. Binary Search in Sorted Array: Implementing binary search using tail recursion is feasible. The function compares the target element with the middle element, and based on that, it performs the search in the left or right subarray through recursive calls. Reversing a List: Reversing a list using tail recursion is possible. The function takes the first element and adds it to the end of the reversed sublist in each recursive call. String Reversal: Reversing a string using tail recursion is also possible. The function takes the first character of the string and adds it to the end of the reversed substring in each recursive call. Counting List Elements: Counting the number of elements in a list using tail recursion is another example. The function increments a counter for each element and recursively calls itself with the rest of the list. Tree Traversal: In certain cases, tree traversal algorithms like post-order traversal can be implemented using tail recursion. The function visits the left and right subtrees and then processes the current node in a tail-recursive manner. Generating Permutations: Generating permutations of a set using tail recursion is possible. The function swaps elements in the set and recursively generates permutations of the remaining elements. Generating Combinations: Generating combinations of elements using tail recursion is also feasible. The function recursively generates combinations by including or excluding each element. Example of the tail recursion in C:Example 1: Printing factorial of a number using tail recursion.Output: 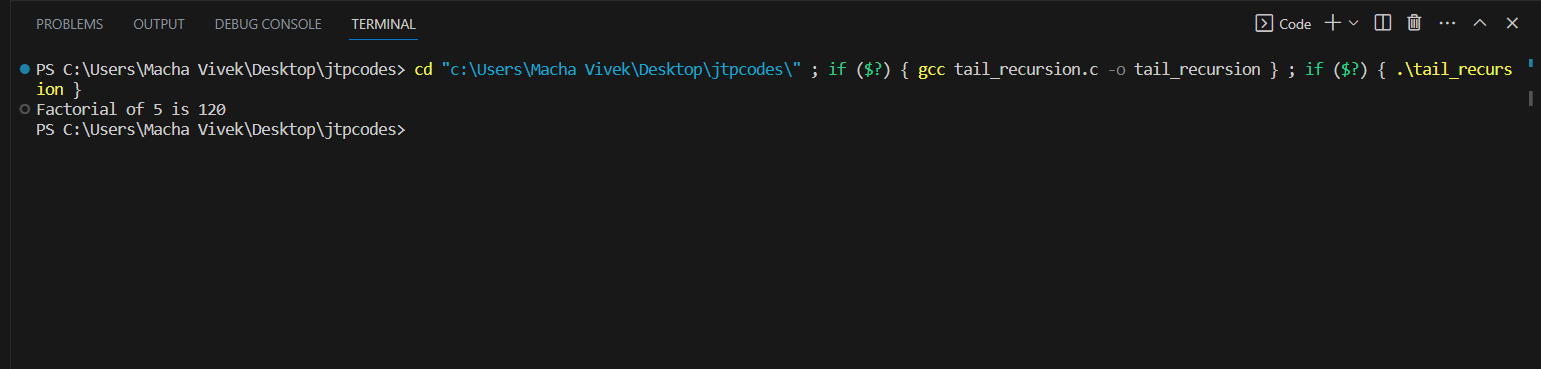
Explanation: In this example, the function starts by checking if the current value of "n" is 0. If it is, it doesn't keep multiplying anymore; it just returns the "accumulator" that has been building up. It is the base case that stops the recursion. If "n" is not 0, the function calculates the product of "n" and the "accumulator". After that, it makes a new call to itself, but with a smaller value of "n" and the new result as the "accumulator". Its process keeps happening until "n" becomes 0. Each time, the function calls itself, and it's like taking a small step toward solving the problem. The recursive call happens as the very last action in the function, known as tail recursion. Tail recursion is smart because it uses memory more efficiently. The computer doesn't need to remember many things because it just focuses on the current step and the new result. This way, it's like doing the multiplications while also counting them. Example 2: Printing Fibonacci sequence using tail recursion.Output: 
Explanation: In this example, the program a function named "fibonacci" to find a specific number in the Fibonacci sequence. This function has three numbers as inputs: "n" (the index of the number you want to find), "a" (the first number in the sequence), and "b" (the second number in the sequence). Inside the "fibonacci" function, there's a condition to check if "n" is 0. If it is, it means you've reached the number you're looking for. So, the function returns the value of "a". If "n" is not 0, the function calculates the next number in the Fibonacci sequence. It can accomplish this by calling itself again but with a different setup. The "a" becomes "b" (the second number), and the "b" becomes the sum of "a" and "b" (the third number). This process keeps repeating until "n" becomes 0. With each recursive call, you're getting closer to finding the Fibonacci number you're interested in. In the "main" function of the code, you set the value of "n" to 6 (which means you want to find the 6th Fibonacci number). After that, you call the "fibonacci" function with the starting numbers 0 and 1. The result of the "fibonacci" function is stored in the "result" variable, and finally, you print out the value of "n" and the Fibonacci number at that index. In simple terms, this code is like an adventure where you follow the Fibonacci sequence step by step, and with each step, you're getting closer to finding the specific number you're looking for. The result of this code for "n = 6" will be the 6th number in the Fibonacci sequence, which is 8. Example 3: Printing the combinationsOutput: 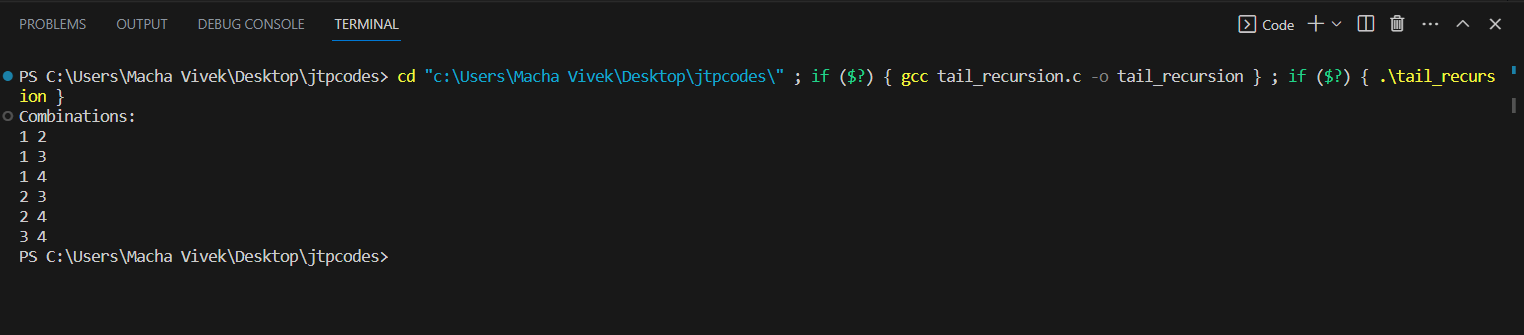
Explanation: In this example, the program takes the "generateCombinations" function to make these combinations. This function needs a few things to work: the original set of numbers ("arr"), the total number of available numbers ("n"), the current position in the combination ("index"), the growing combination itself ("combination"), the desired size of each combination ("k"), and where to start picking numbers ("start"). Inside the "generateCombinations" function, there's a check to see if you've collected enough numbers for a complete combination. If you have, it means you've got a full set, so you print those numbers out and start over to find more combinations. If you haven't collected enough numbers yet, the function starts picking numbers one by one. It picks a number from where you left off and adds it to the "combination". After that, it makes a call to itself, but with one more number in the combination and a new starting point for picking the next number. This process keeps happening, with the function trying different numbers and creating different combinations until it collects enough numbers for a complete set. In the "main" function of the code, you have an array of numbers (1, 2, 3, and 4), and you want to create combinations of 2 numbers at a time. After that, you set up an array called "combination" to store each combination, and then you call the "generateCombinations" function to start the process. The function goes through all the possible combinations of size 2 using the provided numbers and prints them out. Example 4: Printing permutations using tail recursion:Output: 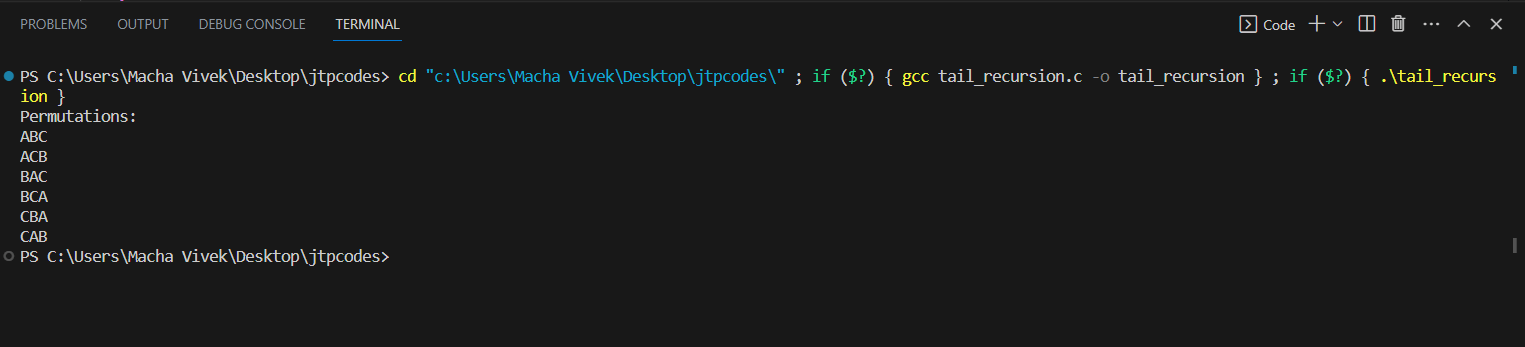
Explanation: In this example, the program takes a function called "swap" that helps you swap the positions of two characters. It's like changing the places of two cards in a deck. After that, you have another function called "generatePermutations". It takes a string of letters ("str"), the starting position for arranging the letters ("start"), and the ending position ("end"). Inside the "generatePermutations" function, there's a check to see if you've reached the end of rearranging the letters. If you have, it means you've created a new arrangement, so you print it out. If you haven't finished yet, the function starts swapping the letters around. It takes one letter and switches it with another. After that, it calls itself, but with the next position to arrange and the same ending position. This process keeps happening, with the function swapping and rearranging letters in all sorts of ways, creating new arrangements each time. After going through all the possible arrangements, the function "backtracks" occurs. It means it undoes the last swap, so it can try different swaps in the next round of arrangements. In the main function, we call the generatePermutations function which is present in the program so that function gives the total permutations of the letters A, B, and C. The function goes through all the possible arrangements of the letters and prints them out individually. Example 5: Post-order tree traversal using tail recursion.Output: 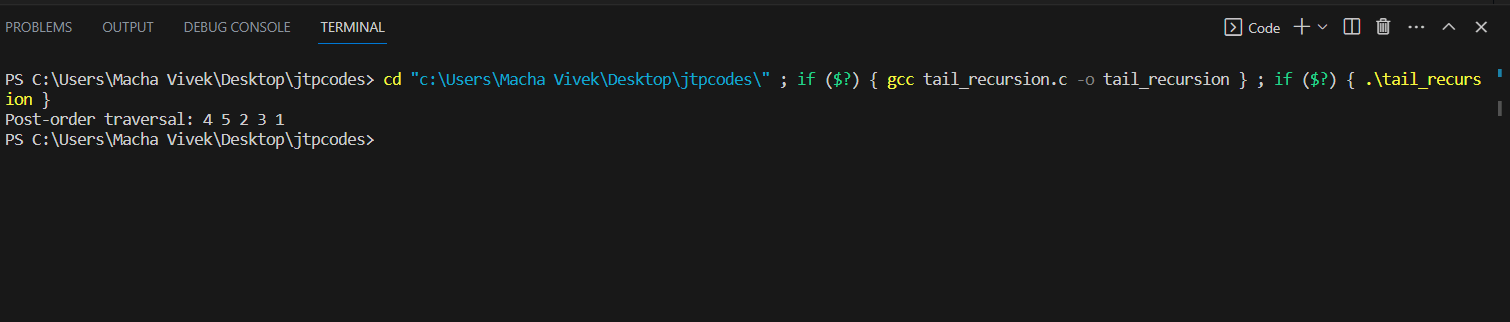
Explanation:struct Node: This line defines a new structure called "Node". It contains the two pointers that are the left and right. These represent the left and right child of the tree given. In this case, a "Node" has an integer value ("data") and two "pointers" to other "Nodes" called "left" and "right". void postOrderTraversal(struct Node* root): This line defines a function named "postOrderTraversal". It takes a "Node" pointer named "root" as input. This function helps you explore the nodes of a "tree" (a special kind of structure). It uses a "post-order" method, which means it first goes to the left, then to the right, and finally processes the current node. if (root == NULL) { return; }: This line checks whether current node (the "root" node) is empty (NULL) or not. If it is, it means you've reached the end of this branch of the tree, so you stop here. postOrderTraversal(root->left); and postOrderTraversal(root->right);: These lines are where the magic happens. The function calls itself twice, once for the left side of the tree ("root->left") and once for the right side ("root->right"). This way, you explore the whole tree using recursion. printf("%d ", root->data);: This line prints the "data" of the current node. In the example, it's the number you stored in the node. It's printed after visiting all the left and right branches because of the post-order traversal. struct Node* createNode(int data): This defines a function called "createNode". It takes an integer value "data" as input and returns a new "Node" that has this data. This function helps you make new nodes for the tree. newNode->data = data;: This line sets the "data" value of the newly created node to the given "data" value. newNode->left = NULL; and newNode->right = NULL;: These lines set the left and right pointers of the new node to NULL. It means that the new node doesn't have any connections yet. int main() {: This is where your program starts executing. It's the "main" function of the program. struct Node* root = createNode(1);: This line creates a new "Node" with the value 1 and stores it in a pointer called "root". root->left = createNode(2); and root->right = createNode(3);: These lines create two more nodes with values 2 and 3 and connect them to the left and right of the "root" node. root->left->left = createNode(4); and root->left->right = createNode(5);: These lines create two nodes with values 4 and 5 and connect them to the left side of the "root's" left node. So, it's like you're building a little tree. printf("Post-order traversal: ");: This line just prints a message to let you know what's coming next. postOrderTraversal(root);: You call the "postOrderTraversal" function with the "root" node as a starting point. This function will explore the entire tree in a post-order method.
Next TopicC program for currency denomination
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share










