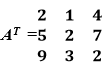Symmetric Matrix in CIntroduction:A square matrix is considered to be symmetric if its transpose equals the supplied matrix. The user can generate a symmetric matrix by switching from row to column and from column to row. Any given matrix A can have its transpose matrix specified as AT. As a result, the condition that A = AT is satisfied by a symmetric matrix A. Transpose Matrix:You may determine its transpose by switching rows and columns in a matrix. The letter "T" is used to represent the matrix's transposition. Example:1If a given matrix is It is a symmetric matrix because A = AT Example:2If a given matrix is It is a symmetric matrix because A ≠ AT Scenario DescriptionLet's create a C program to determine whether a given matrix is symmetric or not. Resolution
Source Code: Here is the source code for the C program that determines whether a matrix is symmetric or not. On a Linux system, the C program is successfully compiled and executed. Also presented below is the output of the program. Output: Please Enter Number of rows and columns: 3 3 Enter the Matrix Elements 1 4 5 4 3 2 5 2 1 The provided matrix is symmetric. Program Description
Case Study:To determine if the matrix is symmetric or not, we input "3" for the number of rows and "3" for the number of columns in this instance. Please Enter Number of rows and columns: 3 3 Enter the Matrix Elements 1 4 5 4 3 2 5 2 1 The provided matrix is symmetric. Time Complexity O(n2)Due to the for loop running n2 times, the above program for determining if a matrix is symmetric or not has an O(n2) time complexity. Space Complexity O(n2)Because n-size 2D arrays have been initialized to hold their values, the space complexity of a 2D array in the program above is O(n2).
Next Topicfgets() function in C
|
 For Videos Join Our Youtube Channel: Join Now
For Videos Join Our Youtube Channel: Join Now
Feedback
- Send your Feedback to [email protected]
Help Others, Please Share





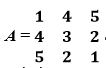 & the transpose of the matrix is
& the transpose of the matrix is 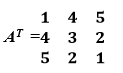
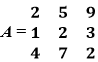 & the transpose of the matrix is
& the transpose of the matrix is