Tower of Hanoi

The Tower of Hanoi puzzle is a captivating challenge that teaches us valuable problem-solving skills and the beauty of recursive thinking. As you delve deeper into its mechanics, understanding the general rules becomes essential for mastering this intriguing puzzle.

Rules of Tower of Hanoi:

1. The Three Pegs: Source, Destination, and Spare:

At the heart of the Tower of Hanoi puzzle are three pegs, often labeled A, B, and C. Each peg can hold the disks, and your goal is to move all the disks from the source peg to the destination peg while using the third peg as a temporary holding area.

2. Disk Sizes and Ordering:

The disks come in different sizes, stacked from largest at the bottom to smallest at the top. This arrangement is critical as it sets the foundation for the puzzle's challenge. You must always ensure that a larger disk is never placed on top of a smaller one during the entire process.

3. The Recursive Algorithm:

The core strategy for solving the Tower of Hanoi puzzle revolves around a simple yet powerful pattern that scales with the number of disks, 'n'. Here's the recursive algorithm:

• Move the top 'n-1' disks from the source peg to the spare peg using the destination peg as an intermediate step.
• Move the largest disk ('n') from the source peg to the destination peg.
• Move the 'n-1' disks from the spare peg to the destination peg using the source peg as an intermediate step.

4. Understanding Recursion:

Recursion is a fundamental concept in computer science and mathematics. It involves breaking down a complex problem into simpler, similar sub-problems. In the context of the Tower of Hanoi, the algorithm keeps applying itself to the smaller sub-problems until it reaches the base case, which is moving a single disk and a task that's easy to achieve.

5. Solving the Puzzle:

Start with the initial configuration of disks on the source peg to solve the Tower of Hanoi puzzle. Apply the recursive algorithm to move the disks from the source peg to the destination peg, adhering to the rules at all times. As you solve the sub-problems, the puzzle gradually transforms into a set of smaller, manageable tasks.

6. The Beauty of Exponential Growth:

One intriguing aspect of the Tower of Hanoi puzzle is the exponential growth in the number of moves required as the number of disks increases. With 'n' disks, the number of moves needed is 2^n - 1. This rapid growth showcases the complex interplay between simple rules and complex outcomes.

7. Patience and Strategy:

While the rules of the Tower of Honzi puzzle are straightforward, successfully completing it requires patience and strategic thinking. You must carefully plan your moves and anticipate the outcomes of each step. The puzzle encourages you to explore various pathways and evaluate the consequences of your decisions.

The puzzle may sound complex, but we can break it down into simple steps:

1. Start with a Single Disk:

Think of the smallest version of this problem: just one disk. Moving a single disk is very simple process. You lift it from the source peg and place it on the destination peg.

2. Two Disks:

Now, imagine you have two disks, labeled 'A' and 'B', stacked on the source peg. To move these disks to the destination peg, you must follow these steps:

• Move disk 'A' from the source peg to the spare peg.
• Move disk 'B' from the source peg to the destination peg.
• Move disk 'A' from the spare peg to the destination peg.

3. Three Disks:

As the number of disks increases, the puzzle becomes more interesting. Let's take three disks: 'A', 'B', and 'C'. Here's how you solve it:

• First, move the top two disks ('A' and 'B') to the spare peg, using the destination peg as an intermediate step. It follows the same steps we used for two disks.
• Now, move the largest disk ('C') to the destination peg.
• Finally, move the two smaller disks ('A' and 'B') from the spare peg to the destination peg using the source peg as an intermediate step.

4. Four Disks:

The pattern continues as you add more disks. For four disks ('A', 'B', 'C', and 'D'), the process looks like this:

• Move the top three disks ('A', 'B', and 'C') to the spare peg using the destination peg as an intermediate step.
• Move the largest disk ('D') to the destination peg.
• Move the three smaller disks ('A', 'B', and 'C') from the spare peg to the destination peg using the source peg as an intermediate step.

Example:

Let's take a program to illustrate the tower of Hanoi problem having 3 pegs:

Output: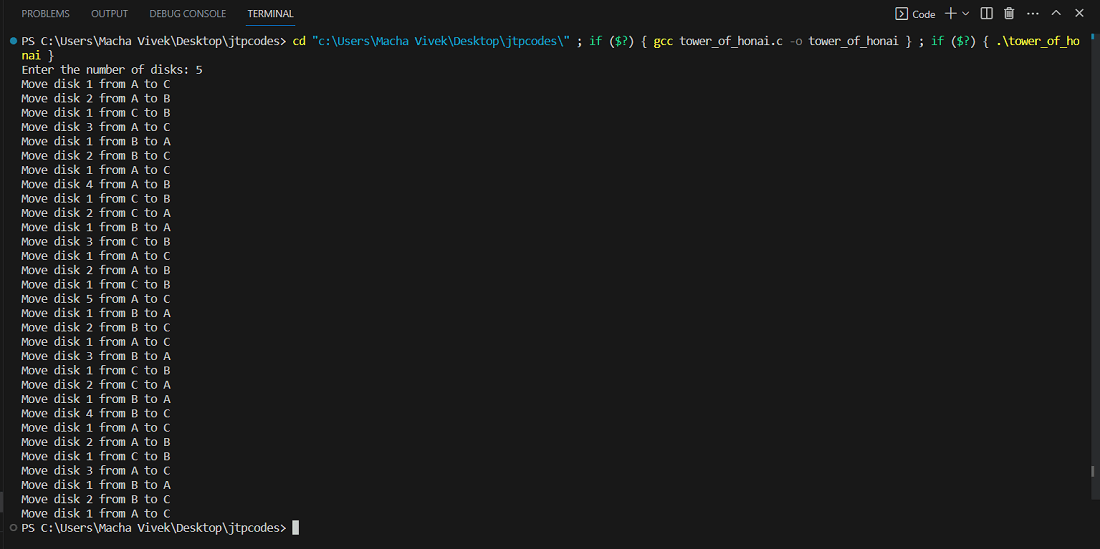

Explanation:

Working of Recursion:

Suppose you have a stack of disks and you want to move from one peg to another, with a spare peg for temporary storage. If you have only one disk, it's simple; you just move it directly. But when you have more than one disk, the recursive magic happens.

If you want to move n disks, you first move the top n-1 disks from the source peg to the spare peg (using the destination peg as temporary storage). It frees up the bottom disk, which you move directly to the destination peg. After that, you move the n-1 disks from the spare peg to the destination peg, using the source peg as temporary storage. It's like solving a smaller version of the same problem twice, once to clear the path for the largest disk and once to move the rest to the destination. This process keeps repeating for each smaller sub-problem until you reach the base case of moving a single disk, which is straightforward. The beauty of recursion is that each sub-problem is solved using the same approach, making the solution elegant and easy to understand.

Variables in the program:

n: The number of disks to be moved.

source: The source peg from which disks are moved.

auxiliary: The auxiliary peg is used for temporary storage.

destination: The destination peg to which disks are moved.

Example:

Let's take a program to illustrate the tower of Hanoi problem having 5 pegs:

Output: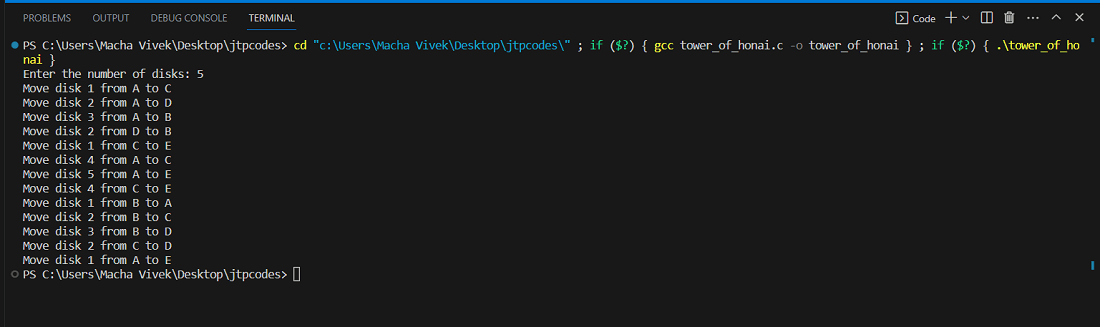

Explanation:

In the traditional Tower of Hanoi problem, you have three pegs (let's call them A, B, and C), and the goal is to move a stack of disks from peg A to peg C, obeying certain rules. Extending this to five pegs introduces additional complexity.

In a five-peg Tower of Hanoi problem, you still have a set of rules to follow:

• You can only move one disk at a time.
• A larger disk cannot be placed on top of a smaller disk.
• You have five pegs instead of three, and you need to move the entire stack from one peg (source) to another peg (destination) using the remaining pegs as temporary storage.

You can use a similar recursive approach to solve this extended problem, but it becomes more intricate. Here's a high-level explanation of the approach:

Base Case: When you have only one disk, you can move it directly from the source peg to the destination peg.

Recursive Step: When you have more than one disk, you need to break down the problem into smaller sub-problems. If you want to move n disks from the source peg to the destination peg using five pegs, you can do the following:

• Move the top n-2 disks to one of the auxiliary pegs.
• Move the (n-1)-th disk to another auxiliary peg.
• Move the n-th disk to the destination peg.
• Move the (n-1)-th disk from the auxiliary peg to the destination peg.
• Move the n-2 disks from the first auxiliary peg to the destination peg.

Recursion: Apply the same strategy recursively to the sub-problems. This process continues until you reach the base case of moving a single disk.

The key challenge in extending the Tower of Hanoi problem to five pegs is keeping track of which pegs to use as auxiliaries and ensuring that the rules of the problem are followed. The recursive approach helps to manage these complexities by solving smaller instances of the problem and combining their solutions to move the entire stack of disks.