Data Structures and Algorithms in C|Set-2

Stacks and Queues

This tutorial will teach two other linear data structures in C-stacks and queues. In the first part of this tutorial, we covered the basics of arrays, dynamic arrays, and linked lists. Both stacks and queues are user-defined, which means that when we say int arr[], the compiler can recognize that it is an array, but when we say Stack, the compiler can't recognize it without us defining it in the program.

Stacks:

Stack is a linear data structure. It is implemented on the principle "LIFO" abbreviation: Last in, first out. It means that the element that is last inserted into a stack will be the first one that gets deleted. A stack only has one opening, which means to insert or delete elements; we need to use the same end. When we insert elements into a stack, we insert elements on top of each other-new elements on the existing element. After inserting all the elements, if we want to delete elements from the Stack, the last element inserted will be the first to come out.

Terminologies:

Inserting an element into the Stack: push
Deleting an element from the Stack: pop
The end/ opening of the Stack: top of the Stack

Functions for stacks:

push(element)	Inserts the specified element into the Stack
pop()	Deletes and returns the element at the top of the Stack
top()	Returns the element at the top of the Stack
peek()	Same as the top()
size()	Returns the size of the specified Stack
empty()	Checks if the given Stack is empty

Push and Pop:

Push and pop are the two major operations on a stack. Hence, let us understand them elaborately:

Suppose we have a stack called "Hundreds".

It's capacity is 10*sizeof(integer) = 40 bytes.

Top index = 3,

top element = 400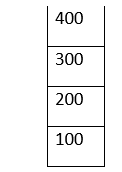

Data Structures and Algorithms in C|Set-2

It has four elements. Now let's perform push and pop on it:

push(Hundreds, 550):

Check if the Stack is full. If it is full, push operation is not possible. Total capacity = 40 bytes. Used capacity = 16 bytes. Hence, the Stack is not filled.
top = top + 1;
Hundreds[top] = 550
Hundreds[4] = 550.

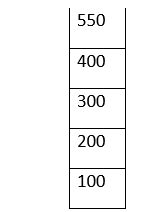
pop():

550 is not a multiple of 100. We mistakenly pushed it into the Stack. It is on the top of the Stack. Now, we need to pop it out.

1. Check if the Stack is empty. If it is empty, we cannot perform the pop operation.

If top_index = -1:

stack is empty

But here, top_index = 4. Hence Stack is not empty.

2. top = top - 1

Hundreds[top]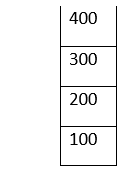

Examples of Stack in Real-Life:

Champagne Tower:
After arranging all the glasses, you can't take the glass from below the tower. It'll collapse the whole tower. Hence, the last glass arranged-the top glass should be the first to be taken-LIFO principle.
Plates:
After piling up plates in the kitchen, we won't take the last plate; we'll take them from the top end.

Implementation of a Stack:

We can implement a stack in 2 ways in C:

Using Arrays
Using Linked lists

1. Using Arrays:

#include<stdio.h>
#include<stdlib.h>
struct stack
{
	int size;
	int top;
	int *array;
};
struct stack* creation(int size)
{
	struct stack* s = (struct stack*)malloc(sizeof(struct stack));
	s -> top = -1;
	s -> size = size;
	s -> array = (int*)malloc(sizeof(int)*size);
	return s;
}
void display(struct stack* s)
{
	int i;
	if(isEmpty(s))
	{
		printf("The stack is empty\n");
	}
	else
	{
		printf("Elements in the stack: \n");
		for(i = s->top; i >= 0; i--)
		{
			printf("%d\n", s->array[i]);
		}
	}
}
int isEmpty(struct stack* s)
{
	int Empty = (s->top == -1);
	
	return Empty;
}
int isFull(struct stack* s)
{
	int Full = (s->top == s->size-1);
	return Full;
}
void push(struct stack* s, int element)
{
	if(isFull(s))
	{
		return;
	}
	int index = ++s->top;
	s->array[index] = element;
	printf("\n%d pushed into the stack\n", element);
	display(s);
}
int pop(struct stack* s)
{
	if(isEmpty(s))
	{
		return INT_MIN;
	}
	int index = s->top--;
	return s->array[index];
}
int peek(struct stack* s)
{
	if(isEmpty(s))
	{
		return INT_MIN;
	}
	int index = s->top;
	return s->array[index];
}
void main()
{
	struct stack* s = creation(50);
	push(s, 100);
	push(s, 200);
	push(s, 300);
	pop(s);
	printf("\nAfter pop operation, elements in the stack: \n");
	display(s);
}

Output:

100 pushed into the Stack
Elements in the Stack:
100

200 pushed into the Stack
Elements in the Stack:
200
100

300 pushed into the Stack
Elements in the Stack:
300
200
100

After the pop operation, elements in the Stack:
Elements in the Stack:
200
100

Like in implementing a linked list, we used a structure to represent Stack. Inside the structure, we created an array. size and top are the properties of the Stack.

2. Using Linked lists:

#include <stdio.h>  
#include <stdlib.h> 
 
//Functions on stack
void push();  
void pop();  
void display(); 

//Stack using Linked list 
struct node   
{  
int data;  
struct node *next;  
};  
struct node *head;  
  
void push () //pushing elements 
{  
    int value;  
    struct node *ptr = (struct node*)malloc(sizeof(struct node));  
     //The last node in the linked list points to NULL 
    if(ptr == NULL)  
    {  
        printf("\nThe stack is already full, can't push more");   
    }  
    else   
    {  
        printf("\n\nEnter a value to push:");  
        scanf("%d", &value);
        //If the Stack is empty  
        if(head == NULL)  
        {         
            ptr -> data = value;  
            ptr -> next = NULL;  
            head = ptr;  
        }   
        else   
        {  
            ptr -> data = value;  
            ptr -> next = head;  
            head = ptr;  
               
        }  
        printf("%d pushed", value);  
    }
    printf("\nResultant stack:");
    display();
}  
  
void pop() //popping element from the stack
{  
    int item;  
    struct node *ptr;  
    if (head == NULL) //empty stack 
    {  
        printf("\nThe stack is empty, can't pop");  
    }  
    else  
    {  
        item = head -> data;  
        ptr = head;  
        head = head -> next;  
        free(ptr);     
    }
    printf("\nResultant stack:");
    display(); 
}  
void display()  
{  
    int i;  
    struct node *ptr;  
    ptr = head;  
    if(ptr == NULL)  
    {  
        printf("\nEmpty stack");  
    }  
    else  
    {  
        printf("\nThe stack: ");  
        while(ptr != NULL)  
        {  
            printf("%d ",ptr -> data);  
            ptr = ptr -> next;  
        }  
    }  
}  
void main()  
{  
    printf("Push operation: ");
    push();
    push();
    push();
    printf("\n\nPop operation: ");
    pop();
}  

Output:

Push operation:

Enter a value to push:100
100 pushed
Resultant Stack:
The Stack: 100

Enter a value to push:200
200 pushed
Resultant Stack:
The Stack: 200 100

Enter a value to push:300
300 pushed
Resultant Stack:
The Stack: 300 200 100

Pop operation:
Resultant Stack:
The Stack: 200 100
--------------------------------
Process exited after 5.783 seconds with return value 0
Press any key to continue . . .

We wrote two methods push and pop, to implement a stack. We need to make sure of two points:

When push is performed, we should always add the elements at the beginning of the linked list. -LI(first in)
When pop is performed, the element from the beginning has to be deleted. -FO(first out)
We created isEmpty() and peek() to check if the Stack is empty because if a stack is empty, we can't perform pop.

Queues:

A queue is a linear data structure like a stack, but the principle of queue implementation is FIFO-First in, first out. It means that the element inserted into the queue will be the first to come out of it, whereas, in a stack, the most recently pushed element will be the first to be popped out.

Important points about a Queue:

There will be two ends to a queue-front and rear ends.
The elements are inserted from the front end and deleted from the rear end.

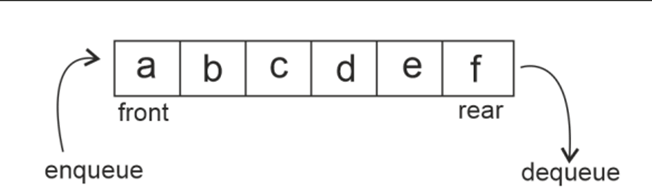
Examples of Queues in Real-Life:

Queues: In our day-to-day lives, we keep seeing people standing in queues at different places like cinema theatres, KFC token counters, etc. The person who started the queue will be the first to get the ticket.
One-way road: The car that enters the lane first will be the first one to exit the lane first.

Terminology:

Inserting an element into a queue: enqueue
Deleting an element from the queue: dequeue
Element at the beginning: front
Element at the end: rear

We can Implement a Queue in C:

Using Arrays
Using linked lists
Using stacks

1. Using Arrays:

#include<stdio.h>   
#include<stdlib.h>   
#define maxsize 10
 
//Functions on queue
void enqueue();  
void dequeue();  
void display();  
int front = -1, rear = -1;
int queue[maxsize];  

//Inserting elements-enqueue
void enqueue()  
{  
    int item;  
    printf("\n\nEnter an element to insert into the queue: ");  
    scanf("%d", &item);  
    //If the queue is filled    
    if(rear == maxsize - 1)  
    {  
        printf("\nThe queue is already full, can't insert more elements");  
        return;  
    }
    //Empty queue
    else if(front == -1 && rear == -1)  
    {  
        front = 0;  
        rear = 0;  
    }  
    else   
    {  
        rear = rear + 1;  
    }  
    queue[rear] = item;  //inserting the element
    printf("%d inserted", item);
    printf("\nThe resultant queue:");
    display();      
}  

//Deleting elements from queue-dequeue
void dequeue()  
{  
    int item;   
    if (front == -1 || front > rear)  //empty queue
    {  
        printf("\nQueue is empty, can't delete elements");  
        return;  
    }  
    else  
    {  
        item = queue[front];  
        if(front == rear)  
        {  
            front = -1;  
            rear = -1 ;  
        }  
        else   
        {  
            front = front + 1;  
        }    
    }  
	printf("\nThe resultant queue:");
	display();   
}  
      
void display()  
{  
    int i;  
    if(rear == -1)  
    {  
        printf("\nEmpty queue");  
    }  
    else  
    {    
        for(i = front; i <= rear; i++)  
        {  
            printf("%d ",queue[i]);  
        }     
    }  
}  

void main ()  
{  
    printf("Enqueue operation:");
    enqueue();
    enqueue();
    enqueue();
    printf("\n\nDequeue operation:");
    dequeue();
}  

Output:

Enqueue operation:

Enter an element to insert into the queue: 100
100 inserted
The resultant queue:100

Enter an element to insert into the queue: 200
200 inserted
The resultant queue:100 200

Enter an element to insert into the queue: 300
300 inserted
The resultant queue:100 200 300

Dequeue operation:
The resultant queue: 200 300
--------------------------------
Process exited after 5.774 seconds with return value 2
Press any key to continue . . .

Observe that two ends, "front" and "rear," are in the queue. Initially initialized to -1, the queue is empty.
For every enqueue operation, we keep adding an index to the queue.
Elements are inserted from the rear end and deleted from the front end.
For every enqueue(): rear = rear + 1
For every dequeue(): front = front + 1

rear: (Inserting order): H - E - L - L - O(0 -> 1 -> 2 -> 3 -> 4)

front: (Deleting order): O - L - L - E - H(4 -> 3 -> 2 -> 1 -> 0)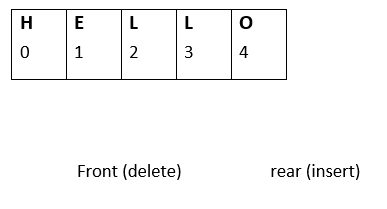

2. Using Linked lists:

#include<stdio.h>   
#include<stdlib.h> 

//Linked list 
struct node   
{  
    int data;   
    struct node *next;  
};  

//Functions and ends in queue
struct node *front;  
struct node *rear;   
void enqueue();  
void dequeue();  
void display();  

void enqueue()  
{  
    struct node *ptr;  
    int item;   
    ptr = (struct node *)malloc(sizeof(struct node));  
    if(ptr == NULL)  //last node in Linked list points to NULL
    {  
        printf("\nQueue is already full, can't insert element");  
        return;  
    }  
    else  
    {   
        printf("\n\nEnter the value to insert: ");  
        scanf("%d", &item);  
        ptr -> data = item;  
        if(front == NULL)  
        {  
            front = ptr;  
            rear = ptr;   
            front -> next = NULL;  
            rear -> next = NULL;  
        }  
        else   
        {  
            rear -> next = ptr;  
            rear = ptr;  
            rear -> next = NULL;  
        }  
    } 
    printf("Resultant queue: ");
    display();
}
     
void dequeue()  
{  
    struct node *ptr;  
    if(front == NULL)  //Empty queue
    {  
        printf("\nThe queue is empty, can't delete from it");  
        return;  
    }  
    else   
    {  
        ptr = front;  
        front = front -> next;  
        free(ptr);  
    }  
    printf("Resultant queue: ");
    display();
} 
 
void display()  
{  
    struct node *ptr;  
    ptr = front;      
    if(front == NULL)  
    {  
        printf("\nEmpty queue");  
    }  
    else  
    {     
        while(ptr != NULL)   
        {  
            printf("%d ",ptr -> data);  
            ptr = ptr -> next;  
        }  
    }  
}  

void main ()  
{  
   printf("Enqueue operation: ");
   enqueue();
   enqueue();
   enqueue();
   printf("\n\nDequeue operation: ");
   dequeue();
   
}  

Output:

Enqueue operation:

Enter the value to insert: 100
Resultant queue: 100

Enter the value to insert: 200
Resultant queue: 100 200

Enter the value to insert: 300
Resultant queue: 100 200 300

Dequeue operation: Resultant queue: 200 300
--------------------------------
Process exited after 4.771 seconds with return value 0
Press any key to continue . . .

Implementation using arrays can't be used for large-scale applications. Hence, linked lists are used to implement queues.
Front and rear are two pointers indicating the ends in the queue. If both front and rear = NULL, the queue is empty.
With every insertion, rear points to the next index(NULL), and with every deletion, front points to the next index.
When inserting elements into the queue, each element is inserted from the end of the linked - FI (first in)
The elements are deleted from the beginning of the linked list. -FO (first out)

3. Using Stacks:

Stacks follow the LIFO principle and queues follow FIFO. So, how does it work?

Let us take an example:

There is a stack, and we pushed elements into it: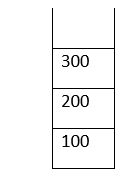

Now, if we perform the pop operation, 300 will be popped. But, as per the queue principle, 100 should be deleted.

We need to take another stack, say, stack2, and pop elements from our Stack to stack2: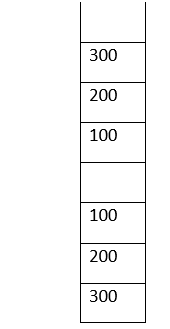

Now, we can pop the elements from stack2. It will be equivalent to the same operation as enqueue in the queue.

We can implement a queue using stacks in two ways:

1. Dequeue operation made costly

In the above example, when we insert the elements into the first Stack, it isn't altered-O(1). But, when we performed dequeue, first we needed to pop the elements to another stack, then from that stack-dequeue operation became costly-O(n).

2. enqueue operation made costly

let us take an example:

We have a stack "stack1" with one element-100:

When we need to perform enqueue on the Stack, all the existing elements in stack1 are popped into stack2.
Say 200 is inserted into stack1. Now, all the elements popped into stack2 are pushed back into stack1.
This way, the first entered element is always kept at the top of stack1 using stack2

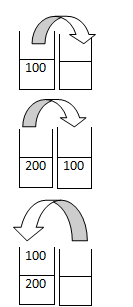
Here is a program implementing using the first way - dequeue operation made costly:

#include<stdio.h>  
#define N 5  

int stack1[5], stack2[5];     
int top1 = -1, top2 = -1;   
int count=0;  
 
//O(1)-normal enqueue operation
void push1(int data)  //pushing the element into the first Stack
{  
 	if(top1 == N-1)  
	{  
   		printf("\nQueue is full, can't insert elements");  
	}	  
	else  
	{	  
   		top1++;   
   		stack1[top1]=data;   
	}  
}  
//Popping elements from stack1
int pop1()  
{     
	if(top1 == -1)  
	{    
	}  
	else  
	{  
   		int temp = stack1[top1];  
   		top1--;   
   		return temp;   
	}  
}   
  //Pushing the popped elements from stack1 to stack2
void push2(int x)  
{    
	if(top2 == N-1)  
	{	    
	}  
	else  
	{  
   		top2++;   
    	stack2[top2] = x;     
	}  
}   
  //Dequeue operation-O(n)
int pop2()  
{  
	int element = stack2[top2];   
   	top2--;   
   	return element;  
}
   
//Queue operations
void enqueue(int element)  
{  
    push1(element); 
    count++;  
}
void dequeue()  
{  
	int i;
   	if((top1 == -1) && (top2 == -1))  
	{	  
   		printf("\nEmpty queue, can't pop");  
	}  
	else  
	{  
		int i;
  		for(i = 0; i < count; i++)  
  		{	  
     			int element = pop1();  
     			push2(element);  
  		}  
		int b = pop2();  
		printf("\nThe deleted element is %d", b);  
		printf("\n");  
		count--;  
		for(i = 0; i < count; i++)  
		{  
   			int a = pop2();  
   			push1(a);   
		}  
	}
} 
 //Displays the elements of the second Stack
void display()  
{  
	int i;
	for(i = 0; i <= top1; i++)  
  	{  
     	printf("%d ", stack1[i]);  
  	}  
}  
void main()  
{  
   enqueue(10); 
   enqueue(20);  
   enqueue(30);
   printf("Enqueue operation-after inserting 10, 20 and 30:");
   display();
   printf("\n\nDequeue operation:");
   dequeue();
   printf("Resultant queue:");  
   display();   
}  

Output:

Enqueue operation-after inserting 10, 20 and 30:10 20 30

Dequeue operation:
The deleted element is 10
Resultant queue:20 30
--------------------------------
Process exited after 0.8232 seconds with return value 1
Press any key to continue . . .

Functions in the program:

push1()	Given an element, it pushes the element into stack1
pop1()	Stores the last element of stack1 in temp and returns it.
push2()	Pushes elements into stack2
pop2()	Pops elements from stack2
enqueue()	Calls push1
dequeue()	Calls push2 with returned temp from pop1() and calls pop2()