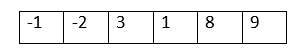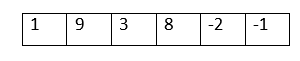Move all negative elements to one side of an Array-C

An Array is homogeneous. An Integer Array can hold negative values, positive values, or zeroes. We need to rearrange the elements of an Array such that all the negative elements go to one side, either to the beginning or end of the Array. The order of the elements is not important here.

This is one of the most frequently asked interview questions, and many approaches exist to solve it. This tutorial lists all the possible ways with examples.

For example, if we're given an Array:

The resultant Array can be:

1. Negative elements to the beginning of the Array:
   
2. Negative elements to the ending of the Array:
   

Note: The order must not be considered. The deal is to have all the negative numbers on one side.

The first approach that comes to mind when hearing the question is the naïve approach-To sort the Array.

If we sort the Array in ascending order, all the negative elements get piled up at the beginning of the Array, and if we sort it in descending order, all the elements get stacked up at the end.

We can use any sorting algorithm to do the sorting. Let us use selection sort:

In the selection sort algorithm, for every element i in the Array, we'll find the minimum element in the sub-Array from i + 1 and swap both the values to sort the Array

Code:

Output:

Enter the size of the Array: 5
Enter the elements: 5 -8 3 -9 2
The final Array: -9 -8 2 3 5

If we follow this approach, the time complexity is O(n²), where n is the Array's length.

Now, let us concentrate on the efficient approaches:

We used nested for loops in the above approach, which increased the time complexity. We need a way to complete the process in one traversal of the Array.

1. Using the partition approach

In this approach, we traverse the Array, and once we find a negative element, we put it at the beginning or end of the Array.

Code:

Output:

Enter the size of the Array: 6
Enter the elements: 1-3 2 -5 -6 -1
The resultant Array: -3 -5 -6 -1 2 1

Understanding:

In the above code, we declared a variable j = 0. arr[j] at the beginning of the Array. Now, we iterate through the Array using i, and in each iteration, we check if arr[i] is negative. If arr[i] is negative, we swap it with arr[j] to send it to the beginning of the Array. Now, we increment the value of j and continue the process.

For example:

Suppose the given Array is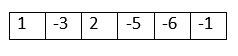

First iteration -> j = 0, i = 0 -> arr[0] is positive

Second iteration -> j = 0, i = 1 -> arr[1] is negative and i != j

so swap arr[0] <-> arr[1]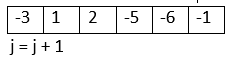

Third iteration -> j = 1, i = 2 -> arr[2] is positive

Fourth iteration -> j = 1, i = 3 -> arr[3] is negative and i != j

so swap arr[1] <-> arr[3]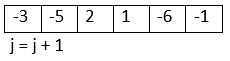

Fifth iteration -> j = 2, i = 4 -> arr[4] is negative and i != j

so swap arr[2] <-> arr[4]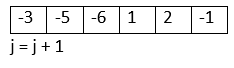

Sixth iteration -> j = 3, i = 5 -> arr[5] is negative and i != j so swap arr[3] <-> arr[5]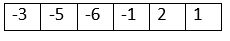

Time complexity: O(n) where n is the size of the Array

2. Using pointers/ variables

In this approach, we use two pointers, or variables, say, a at the beginning and b at the end of the Array. We'll keep checking the elements in the Array by incrementing a and decrementing b.

To get all the negative values to the beginning and positive values to the end of the Array:

Algorithm:

1. If both a and b refer to a negative number, increment a.
2. If a refers to a positive number and b to negative, swap the values at a and b.
3. If both a and b are referring to a positive number, decrement b
4. If a refers to a negative number and b to positive, increment a and decrement b.

Code:

Output:

Enter the size of the Array: 6
Enter the elements: 1 -3 4 -2 4 -3
The resultant Array: -3 -3 -2 4 4 1

3. Dutch Flag Algorithm

Introduced by Dijkstra, given n number of red, white, and blue balls arranged in random order, we need to arrange all the balls such that all the balls of the same color are adjacent to each other. The order of these sets of balls must be in the given order, meaning white balls and then blue balls must follow all the red balls.

We shrink the Array from both sides like the above approach. This code is like a simplification of the above approach:

Code:

Output:

Enter the size of the Array: 6
Enter the elements: 4 -2 4 -1 -2 -5
The resultant Array: -5 -2 -2 -1 4 4

Understanding:

Observe that in the above code, we used the same conditions of the previous approach but simplified it further.