Number of even and odd numbers in a given range

Given a lower limit x and an upper limit y, if we're supposed to count the number of odd and even numbers in the range, we can opt for the regular method of using a for loop and iterating from the lower limit to the upper limit checking if every number in the range is divisible by 2 or not like:

In C:

Output:

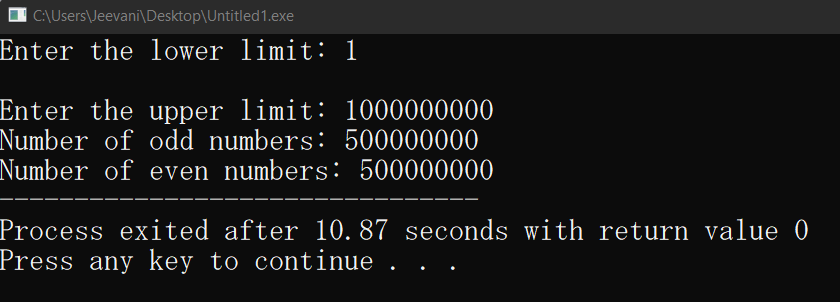
The code works fine when we give small ranges up to some hundreds, but when we try to try larger ranges-higher upper limits, the code takes more time. Like in the above example, it took 10.45 seconds.

Every time to want to write a code, keeping the errors aside, the efficiency of the code is always determined by:

1. Time
2. Space

We should work this out with good logic that doesn't take much time.

Logic:

Let us take cases, and then we'll make a formula ourselves:

Lower limit = L

Upper limit = R

Number of numbers in the range including both limits(N): (R - L + 1)

1. When N is even:
   For Example:
   Lower limit = 10
   Upper limit = 15
   N = 15 - 10 + 1 = 6
   Numbers: [10, 11, 12, 13, 14, 15]
   Number of even numbers: N/2 = 3 = [10, 12, 16]
   Number of odd numbers: N/2 = 3 = [11, 13, 15]
2. When N is odd:
   1. When the lower limit and upper limit are even:
      For example:
      Lower limit = 10
      Upper limit = 16
      N = 16 - 10 + 1 = 7
      Odd numbers = [11, 13, 15] -> 7/2 = 3
      Even numbers = [10, 12, 14, 16] -> N - odd = 7 -3 = 4
   2. When the lower limit and the upper limit are odd:
      For example:
      Lower limit = 11
      Upper limit = 15
      N = 15 - 11 + 1 = 5
      Odd numbers = [11, 13, 15] -> 5/2 + 1 = 3
      Even numbers = [12, 14] -> N - odd = 5 - 3 = 2

So:

1. When we have an even number of numbers in the range, half of them will be even, and the other half will be odd.
2. When we have odd number of numbers:
   1. If both lower and upper limits are even, number of odd numbers: floor(N/2)
   2. If both lower and upper limits are odd, number of odd numbers: floor(N/2) + 1

Let us now design a program with this logic in C:

Output:

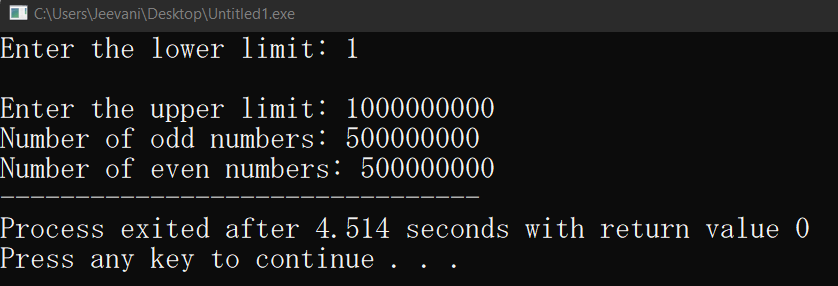
1. We checked if the number of numbers (count) is even, and this happens when the lower limit and upper limit are both of a different kind (even, odd)
   3 4 5 6
   2 3 4 5
2. Now, the two remaining cases are when both the upper limit and upper limit are of the same kind:
   2 3 4 -> Odd numbers: 3/2 = 1
   3 4 5 -> Odd numbers: 3/2 + 1 = 2

We can use Arithmetic progressions too:

By using the n^th term formula of an AP: a + (n - 1)*d

We can find either number of even numbers or the number of odd numbers and then subtract the number from the total number of numbers to find the other number.

Let us work out the code for different cases:

Case1: Lower limit and upper limit are even:

Suppose we're finding the number of even numbers from 10 to 20:

10 11 12 13 14 15 16 17 18 19 20

Observe:

• The numbers are in an AP with d = 1
• The bold numbers are in another AP with d = 2
• So, we can find the position of 20 in the bold AP to find the number of even numbers in the interval:
  20 = 10 + (n - 1)*2
  10 = (n - 1)*2
  5 = (n - 1)
  n = 6
• Now, 11 - 6 = 4 odd numbers.

Case 2: Lower limit and upper limit are odd

Suppose we're finding the number of even numbers from 10 to 20:

11 12 13 14 15 16 17 18 19

Observe:

• The numbers are in an AP with d = 1
• The bold numbers are in another AP with d = 2
• First term = a = a + 1 = 12
• Now, we can find the position of (last term - 1) = 18 to find the number of even numbers like in the previous case:
  18 = 12 + (n - 1)*2
  6 = (n - 1)*2
  3 = (n - 1)
  n = 4
• Now, number of odd numbers = 9 - 4 = 5

Case 3: Odd lower limit and even upper limit

Suppose we're finding the number of even numbers from 10 to 20:

11 12 13 14 15 16 17 18 19 20

Observe:

• The numbers are in an AP with d = 1
• The bold numbers are in another AP with d = 2
• First term = a = a + 1 = 12
• Now, we can find the position of last term = 20 to find the number of even numbers like the first case:
  20 = 12 + (n - 1)*2
  8 = (n - 1)*2
  4 = (n - 1)
  n = 5
• Now, number of odd numbers = 10 - 5 = 5

Case 4: Even lower limit and odd upper limit

Suppose we're finding the number of even numbers from 10 to 20:

12 13 14 15 16 17 18 19 20 21

Observe:

• The numbers are in an AP with d = 1
• The bold numbers are in another AP with d = 2
• First term = a = 12
• Now, we can find the position of last term -1 = 20 to find the number of even numbers like the first case:
  20 = 12 + (n - 1)*2
  8 = (n - 1)*2
  4 = (n - 1)
  n = 5
• Now, number of odd numbers = 10 - 5 = 5

So, keeping it all in one place:

1. If both the lower limit and upper limit are even, we can use the n^th-term formula directly
2. If either the lower limit or upper limit is odd, we need to modify the limits:
   lower = lower + 1
   upper = upper - 1

Program:

Output:

Enter the lower limit: 10
Enter the upper limit: 20
Number of even numbers: 6
Number of odd numbers: 5

Programming skills are all about thinking capabilities. Observe that both the approaches we discussed above are similar.