Bisection Method in C

This section will discuss the bisection method in the C programming language. The bisection method is a simple and convergence method used to get the real roots of non-linear equations. The Bisection method repeatedly bisects or separates the interval and selects a subinterval in which the root of the given equation is found.

It means if a function f(x) is continuous in the closed interval [a, b] and the f(a) and f(b) are two real numbers of opposite signs that contain at least one real root of f(x) = 0, between a and b. This method is also known as the Bolzano or Half Interval or Binary search method.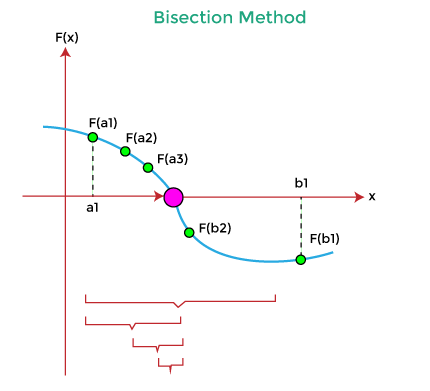

Bisection Method Algorithm:

Following is the algorithm of the Bisection Method in C.

Start the program.
Input two initial guesses x1 and x2. The 'e' is the absolute error to get the desired degree of accuracy.
Compute the function value: f1 = f(x1) and f2 = f(x2)
Now compare the product of f1 and f2 with 0, as

If (f1 * f2) > 0, it displays the initial guesses are wrong and transfer control to step 11.

Get the mid value: x = (x1 + x2) / 2
If ( [ (x1 - x2) / x] < e), then print the value x and jump to (11).
Else, it shows: f = f(x)
If (( f * f1) > 0), then assign x1 = x and f1 = f.
Else, assign x2 = x and f2 = f.
Jump to 5. And the loop continues with new values.
Terminate the program.

Example 1: Program to find the root of the given equation using the Bisection method

Let's consider an example to get the approximation root of an equation using the Bisection method and for loop in the C programming language.

/* program to demonstrate the usage of the bisection method in C. */
#include <stdio.h>

// funciton definition 
void bisect (float *mid_pt, float int_st, float int_end, int *iter_cnt);
double get_fun (double res);


int main ()
{
	// declaration of the variables
	int iter_cnt, mx_iter_cnt;
	float mid_pt, int_st, int_end, err_all, root;
	
	printf (" \n Enter the first starting point: ");
	scanf (" %f", &int_st);
	printf (" \n Enter the second ending point: ");
	scanf (" %f", &int_end);
	
	// declare no. of iteration to be allowed
	printf (" \n Enter the maximum iteration to be allowed: ");
	scanf (" %d", &mx_iter_cnt);
	
	// allow no. of error point
	printf (" Input the no. of allowed error point: ");
	scanf (" %f", &err_all);
	
	// call bisect() function
	bisect (&mid_pt, int_st, int_end, &iter_cnt);
	
	// use for loop to print the max iteration
	for (iter_cnt = 0; iter_cnt < mx_iter_cnt; mid_pt = root)
	{
		
		// chcck initial num * mid_pt is less than 0
		if ( get_fun (int_st) * get_fun (mid_pt) < 0)
		{
			int_end = mid_pt; // assign the mid_pt to int_end
		}
		else
		{
			int_st = mid_pt; // else it assign the mid_pt to int_st
		}
		
		bisect ( &root, int_st, int_end, &iter_cnt); // get the address
		if ( fabs (root - mid_pt) < err_all)
		{
			printf (" \n The approximation root is: %f \n", root);
			return 0;
		}
	}
	
	// print insufficient
	printf (" The iterations are insufficient: ");
	return 0;
}

// function definition
void bisect (float *mid_pt, float int_st, float int_end, int *iter_cnt)
{
	*mid_pt = (int_st + int_end) / 2; // get the middle value
	++(*iter_cnt); // increment the iteration value
	printf ( " Iteration \t %d: \t %f \n", *iter_cnt, *mid_pt);
}

double get_fun (double res)
{
	return (res * res * res - 4 * res - 9);
}

Output:

Enter the first starting point: 5
Enter the second ending point: 9
Enter the maximum iteration to be allowed: 8
Input the no. of allowed error point: 0.02
Iteration	1:	7.000000
Iteration	1: 	8.000000
Iteration	2: 	8.500000
Iteration	3: 	8.750000
Iteration	4: 	8.875000
Iteration	5: 	8.937500
Iteration	6: 	8.968750
Iteration	7: 	8.984375

The approximation root is: 8.984375

Example 2: Program to find the real root of the (x³ + 3x - 5 = 0) equation using the Bisection method

Let's consider an example to print the real roots using the Bisection method in the C programming language.

#include <stdio.h>
#include <conio.h>

// create a function
double bisect ( double num)
{
	// it returns the value of the function
	return ( pow (num, 3) + 3 * num - 5);
}

int main ()
{
	printf ( " \n Display the real roots of the given equation using the Bisection method: ");
	printf ( " \n x ^ 3 + 3 * x - 5 = 0 \n ");
	double x0, x1;
	
	printf ( " \n Enter the first approximation of the root: ");
	scanf (" %lf", &x0);
	
	
	printf ( " \n Enter the second approximation of the root: ");
	scanf (" %lf", &x1);
	
	int iterate;
	printf (" \n Input the number of iteration you want to perform: ");
	scanf (" %d", &iterate);
	
	
	int count = 1;
	double l1 = x0;
	double l2 = x1;
	double r, f1, f2, f3;
	
	// now check whether the initial approximation are the real root
	if (bisect (l1) == 0) // it is a root
	{
		r = l1;
	}
	else if ( bisect (l2) == 0)
	{
		r = l2;
	}
	
	// if the above two values are not the root of the given equation
	else
	{
		while (count <= iterate) // here count is initialized with 1
		{
			f1 = bisect (l1);
			r = (l1 + l2) / 2.0; // get the mid value of the interval l1 and l2
			f2 = bisect (r);
			f3 = bisect (l2);
			
			// check f2 is equal to 0
			if (f2 == 0)
			{
				r = f2;
				break; // break the execution from the while loop statement
			}
			
			printf (" \n The root after %d iterations is %lf. \n", count, r);
			
			// check multiplication of f1 * f2 not less than 0
			if ( f1 * f2 < 0)
			{
				l2 = r;
			}
			else if (f2 * f3 < 0)
			{
				l1 = r;
			}
			count++;
		}
	}	
	// return final value after mentioned the iteration
	printf (" \n The approximation of the root is: %lf \n ", r);	
	return 0;
}  

Output:

Display the real roots of the given equation using the Bisection method:
X ^ 3 + 3 * x - 5 = 0
Enter the first approximation of the root: 1
Enter the second approximation of the root: 5
Input the number of iteration you want to perform: 7
The root after 1 iterations is 3.000000
The root after 2 iterations is 2.000000.
The root after 3 iterations is 1.500000.
The root after 4 iterations is 1.250000.
The root after 5 iterations is 1.125000.
The root after 6 iterations is 1.187500.
The root after 7 iterations is 1.156250.
The approximation root is 1.156250

Example 3: Program to find the approximation root of the non-algebraic function using the Bisection method

Let's create a simple program to calculate the approximation root using the Bisection method and do while loop in C programming language.

/* program to get the roots of the given equation using the do while loop in C. */
#include <stdio.h>
#include <conio.h>
#include <stdlib.h>
#include <math.h>
// define function whose root to be determined
double f (double a)
{
	return 3 * a + sin (a) - exp (a); 
}

int main ()
{
	// declare double data type variable
	double x, y, z, eps;
	int count; // integer data type
	
	x:printf (" \n Input the initial approximation for x: \n ");
	scanf (" %lf", &x);
	
	printf (" Input the initial approximation for y: \n ");
	scanf (" %lf", &y);
	
	printf (" Define the input accuracy: \n ");
	scanf (" %lf", &eps);
	
	printf (" Input the maximum number of iteration: \n ");
	scanf (" %d", &count);
	
	// use if statement to check the product of f(a) and f(b) is not less than 0
	if (f(x) * f(y) <= 0)
	{
		int iter = 1; // initialize iter to 1
		// execution of the bisection method starts here
		
		printf (" Iteration \t x \t \ty \t\tz \t\tf(z) \t |x - y| \n ");
		
		// use do while loop
		do {
			z = (x + y) / 2; // get the mid value for z
			printf (" %d \t %lf \t %lf \t %lf \t %lf \t %lf \n", iter, x, y, z, f(z), fabs(x - y));
			if (f(x) * f(z) > 0)
			{
				x = z; // assign the value of z to x
			}
			else if (f(x) * f(z) < 0)
			{
				y = z; // assign the value of z to y
			}
			iter++; // increment counter by 1
		}
		while (fabs (x - y) >= eps && iter <= count);
		printf (" \nThe root of the given equation is: %lf", z);
	}
	else
	{
		printf (" \n The root doesn't exist in the given interval. ");
		goto x;
	}
		
}

Output:

 Input the initial approximation for x: 
 1
 Input the initial approximation for y: 
 3
 Define the input accuracy: 
 .002
 Input the maximum number of iteration: 
 10
 Iteration 	 x 	 	y 		z 		f(z) 	 |x - y| 
  1 	 1.000000 	 3.000000 	 2.000000 	 -0.479759 	 2.000000 
 2 	 1.000000 	 2.000000 	 1.500000 	 1.015806 	 1.000000 
 3 	 1.500000 	 2.000000 	 1.750000 	 0.479383 	 0.500000 
 4 	 1.750000 	 2.000000 	 1.875000 	 0.058267 	 0.250000 
 5 	 1.875000 	 2.000000 	 1.937500 	 -0.195362 	 0.125000 
 6 	 1.875000 	 1.937500 	 1.906250 	 -0.064801 	 0.062500 
 7 	 1.875000 	 1.906250 	 1.890625 	 -0.002343 	 0.031250 
 8 	 1.875000 	 1.890625 	 1.882812 	 0.028192 	 0.015625 
 9 	 1.882812 	 1.890625 	 1.886719 	 0.012982 	 0.007812 
 10 	 1.886719 	 1.890625 	 1.888672 	 0.005334 	 0.003906 
 
The root of the given equation is: 1.888672

Advantages of the Bisection Method:

The Bisection method is guaranteed to the convergence of real roots.
It reduces the chances of error in the non-linear equation.
It evaluates one function at each iteration.
It usually convergence in a linear fashion.
We can control the error by increasing the number of iterations that return a more accurate root in the bisection method.
It does not involve complex calculations to get the root.
The bisection method is faster in the case of multiple roots.

Disadvantages of the Bisection Method

In the Bisection method, the convergence is very slow as compared to other iterative methods.
The rate of approximation of convergence in the bisection method is 0.5.
It is a linear rate of convergence.
It fails to get the complex root.
It cannot be applied if there are any discontinuity occurrs in the guess interval.
It is unable to find the root for some equations. For example, f(x) = x²as there are no bracketing or bisect values.
It cannot be used over an interval when the function takes the same sign values.

Next Topicsnprintf() function in C

← prev next →